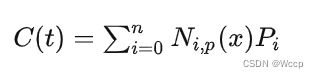B样条曲线
目前我对B样条的运用:对于静态地图,在全局路径规划后,可以用B样条曲线来拟合一个局部路径。所以可以作为局部路径规划来用。
上文讲了贝塞尔曲线,最后也点到了贝塞尔曲线的三个缺点,本文引入了B样条曲线。与贝塞尔曲线不同,B样条曲线可以在拥有贝塞尔曲线的优点下还可以解决贝塞尔的缺点。
具体讲解如下:
公式:
和Bezier曲线的公式相似,曲线上点的坐标是控制点的加权平均值
权重的计算:
先看几张图理解一下:
进一步的理解是:
B样条曲线引入了一组节点U,当u不在Ui-1,Ui+1这个区间内,B=0。
可以这样理解:当u不在两个节点间时,对应控制点的权重为零。也就是说,控制点只对临近的曲线点有影响,对较远的曲线点没有影响,因此解决了Bezier曲线‘牵一发而动全身’的问题。
而根据生成的曲线不同,B样条曲线分为均匀B样条曲线,准均匀B样条曲线,分段B样条
均匀B样条曲线:
if flag == 1: # 均匀B样条很简单
NodeVector = np.array([np.linspace(0, 1, n + k + 1)]
) # 均匀B样条节点向量,首末值定义为 0 和 1
for u in np.arange((k-1) / (n + k+1 ), (n + 2) / (n + k+1 ), 0.001):
for i in range(n+1):
Bik_u[i, 0] = BaseFunction(i, k, u, NodeVector)
p_u = P.T @ Bik_u
path.append(p_u)均匀B样条曲线中,U中的节点间隔是均匀的,但是并不一定是从0到1。
准均匀B样条曲线:
def U_quasi_uniform(n=None, k=None):
"""准均匀B样条的节点向量计算
首末值定义为 0 和 1
Args:
n (_type_, optional): n表示控制点个数-1,控制点共n+1个. Defaults to None.
k (_type_, optional): B样条阶数k, k阶B样条,k-1次曲线. Defaults to None.
Returns:
_type_: _description_
"""
# 准均匀B样条的节点向量计算,共n+1个控制顶点,k-1次B样条,k阶
NodeVector = np.zeros((1, n + k + 1))
piecewise = n - k + 2 # B样条曲线的段数:控制点个数-次数
if piecewise == 1: # 只有一段曲线时,n = k-1
NodeVector[0, n + 1:n + k + 1] = 1
else:
for i in range(n - k + 1): # 中间段内节点均匀分布:两端共2k个节点,中间还剩(n+k+1-2k=n-k+1)个节点
NodeVector[0, k + i] = NodeVector[0, k + i - 1] + 1 / piecewise
NodeVector[0, n + 1:n + k + 1] = 1 # 末尾重复度k
return NodeVector
elif flag == 2:# 准均匀
NodeVector = U_quasi_uniform(n, k)
for u in np.arange(0, 1, 0.005):
for i in range(n+1):
Bik_u[i, 0] = BaseFunction(i, k, u, NodeVector)
p_u = P.T @ Bik_u
path.append(p_u)准均匀B样条曲线中,两端节点有重复度K,中间节点非递减序列,准均匀B样条保留了在两个端点处的性质,样条曲线在端点处的切线为倒数两个端点的连线。从我的理解来看,其实准均匀中两端的重复就是因为在往下递归过程中两端的点相比于其他点会少一部分点,而产生在端点处的不完整性,准均匀B样条这样,在两端重复K次,可以弥补。这只是我的理解,我对B样条的理解也不是很多。
分段B样条曲线:
def U_piecewise_B_Spline(n=None, k=None):
"""分段B样条的节点向量计算
首末值定义为 0 和 1
# 分段Bezier曲线的节点向量计算,共n+1个控制顶点,k阶B样条,k-1次曲线
# 分段Bezier端节点重复度为k,内间节点重复度为k-1,且满足n/(k-1)为正整数
Args:
n (_type_, optional): 控制点个数-1,控制点共n+1个. Defaults to None.
k (_type_, optional): B样条阶数k, k阶B样条,k-1次曲线. Defaults to None.
Returns:
_type_: _description_
"""
NodeVector = np.zeros((1, n + k + 1))
if n%(k-1) == 0 and k-1 > 0: # 满足n是k-1的整数倍且k-1为正整数
NodeVector[0, n + 1:n + k + 1] = 1 # 末尾n+1到n+k的数重复
piecewise = n / (k - 1) # 设定内节点的值
if piecewise > 1:
# for i in range(k-1): # 内节点重复k-1次
NodeVector[0, k:n + 1] = 1 / piecewise # 内节点重复度k-1
else:
print('error!\n' % ())
return NodeVector
elif flag == 3:
NodeVector = U_piecewise_B_Spline(n, k)
for u in np.arange(0, 1, 0.005):
for i in range(n+1):
Bik_u[i, 0] = BaseFunction(i, k, u, NodeVector)
p_u = P.T @ Bik_u
path.append(p_u)
其实这三种B样条曲线,似乎就是一组节点U不同。