剑指 Offer II 112. 最长递增路径（困难 图 dfs 动态规划）

剑指 Offer II 112. 最长递增路径

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

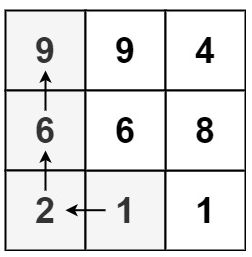
输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4
解释：最长递增路径为 [1, 2, 6, 9]。
示例 2：

输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
示例 3：

输入：matrix = [[1]]
输出：1

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
0 <= matrix[i][j] <= 231 - 1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/fpTFWP
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

分析

1、题目要求按照递增的路径走，那么整个矩阵可以看成有向无环图，要求最长的路径，使用深度优先搜索。由于图是无环的，所以不必记录访问过的节点，因为不可能重复访问。
2、题目是找最长的递增路径，我们需要遍历整个矩阵找到每个节点的最长路径，为了避免遍历重复的路径，可以创建一个跟矩阵相同大小的数组 lengths 用来记录已经走过的节点对应的最长路径。
3、dfs 方法搜索思路：首先递归的返回条件是 lengths[i][j] != 0，即节点 (i, j) 处的最长路径已经找到了，可以返回了，返回 lengths[i][j]；如果还没找到就进行寻找，用变量 length 记录最长的路径，初始值为 1，因为路径最小为 1，对 (i ,j) 的上下左右四个方向进行判断，对于大于节点 (i, j) 的值的方向进行递归直到递增路径的终点（或者到达已经被记录的节点，在递归的开始会直接返回，类似动态规划的思想），在完成所有的递归后，length 应该为我们要找的最长路径，赋值 lengths[i][j] = length 即可。

题解（Java）

class Solution {
    private int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};

    public int longestIncreasingPath(int[][] matrix) {
        if (matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }

        int[][] lengths = new int[matrix.length][matrix[0].length];
        int max = 0;
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                max = Math.max(max, dfs(matrix, lengths, i, j));
            }
        }

        return max;
    }

    private int dfs(int[][] matrix, int[][] lengths, int i, int j) {
        if (lengths[i][j] != 0) {
            return lengths[i][j];
        }

        int rows = matrix.length;
        int cols = matrix[0].length;
        int length = 1;
        for (int[] dir : dirs) {
            int r = i + dir[0];
            int c = j + dir[1];
            if (r >= 0 && r < rows && c >= 0 && c < cols && matrix[i][j] < matrix[r][c]) {
                int path = dfs(matrix, lengths, r, c);
                length = Math.max(path + 1, length);
            }
        }

        lengths[i][j] = length;
        return length;
    }
}