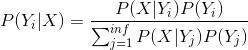NLP系列——(5)朴素贝叶斯+SVM+LDA

一、朴素贝叶斯

1.1 朴素贝叶斯理论

朴素贝叶斯的原理：
基于朴素贝叶斯公式，比较出后验概率的最大值来进行分类，后验概率的计算是由先验概率与类条件概率的乘积得出，先验概率和类条件概率要通过训练数据集得出，即为朴素贝叶斯分类模型，将其保存为中间结果，测试文档进行分类时调用这个中间结果得出后验概率。

那什么是朴素贝叶斯？
贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单，也是常见的一种分类方法。
贝叶斯公式：
X：特征向量，Y：类别

先验概率 P(X)：是指根据以往经验和分析得到的概率。
后验概率 P(Y|X)：事情已经发生，要求这件事情发生的原因是由某个因素引起的可能性的大小。
类条件概率 P(X|Y)：在已知某类别的特征空间中，出现特征值X的概率密度。

朴素：朴素贝叶斯算法是假设哥哥特征之间相互独立，也是朴素的意思。由此，P(X|Y)就可以写成：

朴素贝叶斯公式：

模型原理与训练

• 朴素贝叶斯分类器是一种有监督学习，常见有三种模型，多项式模型(multinomial model)即为词频型和伯努利模型(Bernoulli model)即文档型，还有一种高斯模型。
• 前二者的计算粒度不一样，多项式模型以单词为粒度，伯努利模型以文件为粒度，因此二者的先验概率和类条件概率的计算方法都不同。计算后验概率时，对于一个文档d，多项式模型中，只有在d中出现过的单词，才会参与后验概率计算，伯努利模型中，没有在d中出现，但是在全局单词表中出现的单词，也会参与计算，不过是作为“反方”参与的。
• 这里暂不考虑特征抽取、为避免消除测试文档时类条件概率中有为0现象而做的取对数等问题。

1.高斯模型

有些特征可能是连续型变量，比如说人的身高，物体的长度，这些特征可以转换成离散型的值，比如如果身高在160cm以下，特征值为1；在160cm和170cm之间，特征值为2；在170cm之上，特征值为3。也可以这样转换，将身高转换为3个特征，分别是f1、f2、f3，如果身高是160cm以下，这三个特征的值分别是1、0、0，若身高在170cm之上，这三个特征的值分别是0、0、1。不过这些方式都不够细腻，高斯模型可以解决这个问题。高斯模型假设这些一个特征的所有属于某个类别的观测值符合高斯分布，也就是：

from sklearn.naive_bayes import GaussianNB
#高斯贝叶斯
def train_model_GaussianNB():
    pass
    clf3 = GaussianNB()
    clf3.fit(X[499:], y[499:])#训练模型
    predict_labels = clf3.predict(X[0:499])
    # 预测对了几个？
    n = 0
    for i in range(len(predict_labels)):
        if (predict_labels[i] == y[i]):
            n = n + 1
    print("高斯贝叶斯:")
    # 正确率
    print(n / 499.0)
    # 混淆矩阵
    confusion_matrix(y[0:499], predict_labels)
    return

2.多项式模型

在多项式模型中，设某文档d=(t₁,t₂,…,t_k)，t_k是该文档中出现过的单词，允许重复，则先验概率P©= 类c下单词总数/整个训练样本的单词总数。类条件概率P(t_k|c)=(类c下单词t_k在各个文档中出现过的次数之和+1)/(类c下单词总数+|V|)。
其中V是训练样本的单词表（即抽取单词，单词出现多次，只算一个），|V|则表示训练样本包含多少种单词。P(t_k|c)可以看作是单词t_k在证明d属于类c上提供了多大的证据，而P©则可以认为是类别c在整体上占多大比例(有多大可能性)。

 
from sklearn.naive_bayes import MultinomialNB
#多项式贝叶斯
def train_model_MultinomialNB():
    pass
    clf = MultinomialNB()
    #训练模型
    clf.fit(X[499:],y[499:])
    #预测训练集
    predict_labels = clf.predict(X[0:499])
    #预测对了几个？
    n = 0
    for i in range(len(predict_labels)):
        if(predict_labels[i] == y[i]):
            n = n + 1
    print("多项式贝叶斯:")
    #正确率
    print (n/499.0)
    #混淆矩阵
    confusion_matrix(y[0:499], predict_labels)
    return

3.伯努利模型

P©= 类c下文件总数/整个训练样本的文件总数
P(t_k|c)=(类c下包含单词t_k的文件数+1)/(类c下包含的文件+2)

from sklearn.naive_bayes import BernoulliNB
#伯努利贝叶斯
def train_model_BernoulliNB():
    pass
    clf2 = BernoulliNB()
    clf2.fit(X[499:], y[499:])
    predict_labels = clf2.predict(X[0:499])
    # 预测对了几个？
    n = 0
    for i in range(len(predict_labels)):
        if (predict_labels[i] == y[i]):
            n = n + 1
    print("伯努利贝叶斯:")
    # 正确率
    print (n / 499.0)
    # 混淆矩阵
    confusion_matrix(y[0:499], predict_labels)
    return

文本分类是作为离散型数据的。朴素贝叶斯用于很多方面，数据就会有连续和离散的，连续型时可用正态分布，还可用区间，将数据的各属性分成几个区间段进行概率计算，测试时看其属性的值在哪个区间就用哪个条件概率。再有TF、TDIDF，这些只是描述事物属性时的不同计算方法，例如文本分类时，可以用单词在本文档中出现的次数描述一个文档，可以用出现还是没出现即0和1来描述，还可以用单词在本类文档中出现的次数与这个单词在剩余类出现的次数（降低此属性对某类的重要性）相结合来表述。
参见

1.2 朴素贝叶斯实战——文本分类

使用朴素贝叶斯分类器对新闻文本数据进行类别预测

# 从sklearn.datasets里导入新闻数据抓取器fetch_20newsgroup
from sklearn.datasets import fetch_20newsgroups
# 与之前预存的数据不同,fetch_20newsgroup需要即时从互联网下载数据
news = fetch_20newsgroups(subset='all')
# 查验数据规模和细节
print (len(news.data))
print (news.data[0])


# 使用sklearn.model_selection里的train_test_split模块用于分割数据
from sklearn.model_selection import train_test_split
# 随机采样25%的数据样本作为测试集
X_train, X_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25, random_state=33)

# 从sklearn.feature_extraction.test里导入用于文本特征向量转化模块
from sklearn.feature_extraction.text import CountVectorizer
vec = CountVectorizer()
X_train = vec.fit_transform(X_train)
X_test = vec.transform(X_test)

# 从sklearn.naive_bayes里导入朴素贝叶斯模型
from sklearn.naive_bayes import MultinomialNB
# 使用默认配置初始化朴素贝叶斯模型
mnb = MultinomialNB()
# 利用训练数据对模型参数进行估计
mnb.fit(X_train, y_train)
# 对测试样本进行类别预测,结果存储在变量y_predict中
y_predict = mnb.predict(X_test)


# 从sklearn.metrics里导入classification_report用于详细的分类性能报告
from sklearn.metrics import classification_report
print('The accuracy of Naive Bayes Classifier is', mnb.score(X_test, y_test))
print (classification_report(y_test, y_predict, target_names=news.target_names))

二、SVM模型

2.1 SVM原理

支持向量机（SVM，也称为支持向量网络），是机器学习中获得关注最多的算法之一。它源于统计学习理论，是我们除了集成算法之外，接触的第一个强学习器。它有多强呢？
从算法的功能来看，SVM几乎囊括了所有普通算法的功能。

领域	功能
有监督学习	线性二分类与多分类（Linear Support Vector Classification）； 非线性二分类与多分类（Support Vector Classification, SVC） ；普通连续型变量的回归（Support Vector Regression）；概率型连续变量的回归（Bayesian SVM）
无监督学习	支持向量聚类（Support Vector Clustering，SVC）；异常值检测（One-class SVM）
半监督学习	转导支持向量机（Transductive Support Vector Machines，TSVM）

从实际应用来看，SVM在各种实际问题中都表现非常优秀。它在手写识别数字和人脸识别中应用广泛，在文本和超文本的分类中举足轻重，因为SVM可以大量减少标准归纳（standard inductive）和转换设置（transductive settings）中对标记训练实例的需求。同时，SVM也被用来执行图像的分类，并用于图像分割系统。实验结果表明，在仅仅三到四轮相关反馈之后，SVM就能实现比传统的查询细化方案（query refinement schemes）高出一大截的搜索精度。除此之外，生物学和许多其他科学都是SVM的青睐者，SVM现在已经广泛被用于蛋白质分类，现在化合物分类的业界平均水平可以达到90%以上的准确率。在生物科学的尖端研究中，人们还使用支持向量机来识别用于模型预测的各种特征，以找出各种基因表现结果的影响因素。
从学术的角度来看，SVM是最接近深度学习的机器学习算法。线性SVM可以看成是神经网络的单个神经元（虽然损失函数与神经网络不同），非线性的SVM则与两层的神经网络相当，非线性的SVM中如果添加多个核函数，则可以模仿多层的神经网络。
从数学的角度来看，SVM的数学原理是公认的对初学者来说难于上青天的水平，对于没有数学基础和数学逻辑熏陶的人来说，探究SVM的数学原理本身宛如在知识的荒原上跋涉。

参见：https://blog.csdn.net/herosunly/article/details/89337079
https://blog.csdn.net/d__760/article/details/80387432

2.2 SVM实战——文本分类

利用SVM结合 Tf-idf 算法进行文本分类

1、读取数据

from sklearn.datasets import fetch_20newsgroups
import numpy as np
import pandas as pd

#初次使用这个数据集的时候，会在实例化的时候开始下载
data = fetch_20newsgroups()

categories = ["sci.space" #科学技术 - 太空
,"rec.sport.hockey" #运动 - 曲棍球
,"talk.politics.guns" #政治 - 枪支问题
,"talk.politics.mideast"] #政治 - 中东问题
train = fetch_20newsgroups(subset="train",categories = categories)
test = fetch_20newsgroups(subset="test",categories = categories)

2、使用TF-IDF将文本数据编码

from sklearn.feature_extraction.text import TfidfVectorizer as TFIDF

Xtrain = train.data
Xtest = test.data
Ytrain = train.target
Ytest = test.target
tfidf = TFIDF().fit(Xtrain)
Xtrain_ = tfidf.transform(Xtrain)
Xtest_ = tfidf.transform(Xtest)
print(Xtrain_)
tosee = pd.DataFrame(Xtrain_.toarray(),columns=tfidf.get_feature_names())
tosee.head()
tosee.shape

3、SVM建模

from sklearn.svm import SVC

clf = SVC()
clf.fit(Xtrain_,Ytrain)
y_pred = clf.predict(Xtest_)
proba = clf.predict_proba(Xtest_)
score = clf.score(Xtest_,Ytest)

print("\tAccuracy:{:.3f}".format(score))
print("\n")

三、LDA主题模型

3.1 PLSA、共轭先验分布

3.1.1 PLSA(基于概率统计的隐性语义分析)

PLSA(Probabilistic Latent Semantic Analysis，基于概率统计的隐性语义分析)。在介绍PLSA之前，先介绍LSA(隐性语义分析)。LSA的目的是要从文本中发现隐含的语义维度，即"Topic"或"Concept"。在文档的空间向量模型中，文档被表示成由特征词出现概率组成的多维向量，这种方法的好处是可以将query和文档转化为同一空间下的向量计算相似度，可以对不同词项赋予不同的权重，在文本检索、分类、聚类问题中都得到了广泛的应用。然而，向量空间模型没有能力处理一词多义和一义多词问题，例如同义词也分别被表示成独立的一维，计算向量的余弦相似度时会低估用户期望的相似度，而某个词项有多个词义时，始终对应同一维度，因此计算的结果会高估用户期望的相似度。

LSA方法的引入可以减轻类似的问题。LSA的核心思想是将词和文档映射到潜在语义空间，再比较其相似度。基于SVD分解，我们可以构造一个原始向量矩阵的一个低秩逼近矩阵，具体的做法是将词项文档矩阵做SVD分解。如图：

第一个矩阵 U 中的每一行表示意思相关的一类词，其中的每个非零元素表示这类词中每个词的重要性（或者说相关性），数值越大越相关。最后一个矩阵 V 中的每一列表示同一主题一类文章，其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵 D 则表示类词和文章类之间的相关性。因此，我们只要对关联矩阵 X 进行一次奇异值分解，我们就可以同时完成了近义词分类和文章的分类。（同时得到每类文章和每类词的相关性）。
尽管基于SVD的LSA取得了一定的成功，但其缺乏严谨的数理统计基础，而且SVD分解十分耗时。Hofmann在SIGIR’99上提出了基于概率统计的PLSA模型，并且用EM算法学习模型参数。PLSA的概率图模型如下：

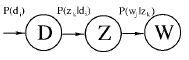
其中D代表文档，Z代表隐含类别或者主题，W为观察到的单词，P(d_i)表示单词出现在文档的概率，P(z_k|d_i)表示文档d_i中出现主题z_k下的单词概率，P(w_j|z_k) 给定主题 z_k 出现单词 w_j 的概率。并且每个主题在所有词项上服从Multinomial分布，每个文档在所有主题上服从Multinomial分布。整个文档的生成过程是这样的：

(1) 以 P(d_i) 的概率选中文档d_i；(2)以P(z_k|d_i)的概率选择主题z_k；(3) 以P(w_j|z_k) 的概率产生一个单词w_j。

我们可以观察到的数据就是(d_i,w_j)对，而z_k是隐含变量。(d_i,w_j)的联合分布为：

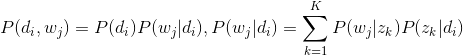
而P(z_k|d_i)和P(w_j|z_k})分布对应了两组Multinomial分布，我们需要估计这组分布的参数。一般会采用EM算法进行参数估计。

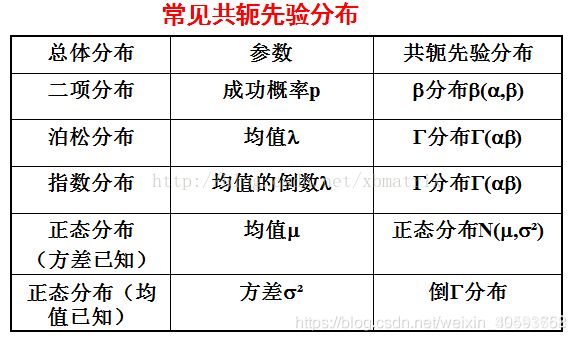
3.1.1 共轭先验分布

在共轭先验分布(Conjugate prior distribution)之前，先复习贝叶斯公式：

其中Y₁,Y₂,…是对样本空间的划分。

先验分布：在抽取样本X之前，需要对样本类别Y有所了解的信息，通常称为先验信息.对于样本类别Y的分布称为先验分布，这里是 P(Y_i);

后验分布：在抽取样本X，得到样本信息的情况下关于样本类别Y的概率分布称为后验信息，这里是P(Y_i|X);

共轭先验分布：在贝叶斯概率理论中，如果后验概率P(Y_i|X)和先验概率P(Y_i)满足同样的分布(形式相同，参数不同)。那么，先验分布和后验分布被叫做共轭分布，同时，先验分布叫做似然函数的共轭先验分布。

常见的共轭先验分布如图：

3.2 LDA

3.2.1 LDA介绍

LDA（Latent Dirichlet Allocation）是一种文档主题生成模型，也称为一个三层贝叶斯概率模型，包含词、主题和文档三层结构。所谓生成模型，就是说，我们认为一篇文章的每个词都是通过“以一定概率选择了某个主题，并从这个主题中以一定概率选择某个词语”这样一个过程得到。文档到主题服从多项式分布，主题到词服从多项式分布。

LDA是一种非监督机器学习技术，可以用来识别大规模文档集（document collection）或语料库（corpus）中潜藏的主题信息。它采用了词袋（bag of words）的方法，这种方法将每一篇文档视为一个词频向量，从而将文本信息转化为了易于建模的数字信息。但是词袋方法没有考虑词与词之间的顺序，这简化了问题的复杂性，同时也为模型的改进提供了契机。每一篇文档代表了一些主题所构成的一个概率分布，而每一个主题又代表了很多单词所构成的一个概率分布。

3.2.2 LDA生成过程

对于语料库中的每篇文档，LDA定义了如下生成过程（generativeprocess）：
(1)对每一篇文档，从主题分布中抽取一个主题;
(2)从上述被抽到的主题所对应的单词分布中抽取一个单词;
(3)重复上述过程直至遍历文档中的每一个单词。
语料库中的每一篇文档与T（通过反复试验等方法事先给定）个主题的一个多项分布 （multinomialdistribution）相对应，将该多项分布记为θ。每个主题又与词汇表（vocabulary）中的V个单词的一个多项分布相对应，将这个多项分布记为φ。

3.2.3 LDA整体流程

文档集合D，主题集合T
D中每个文档d看作一个单词序列，wi表示第i个单词，设d有n个单词。（LDA里面称之为wordbag，实际上每个单词的出现位置对LDA算法无影响）

文档集合D中的所有单词组成一个大集合VOCABULARY(简称VOC)。

LDA以文档集合D作为输入，希望训练出两个结果向量(设聚成k个topic，VOC中共包含m个词)。

对每个D中的文档d，对应到不同Topic的概率θd，其中，pti表示d对应T中第i个topic的概率。计算方法是直观的，pti=nti/n，其中nti表示d中对应第i个topic的词的数目，n是d中所有词的总数。

对每个T中的topic，生成不同单词的概率φt，其中，pwi表示t生成VOC中第i个单词的概率。计算方法同样很直观，pwi=Nwi/N，其中Nwi表示对应到topict的VOC中第i个单词的数目，N表示所有对应到topict的单词总数。

LDA的核心公式如下：

p(w|d)=p(w|t)*p(t|d)

直观的看这个公式，就是以Topic作为中间层，可以通过当前的θd和φt给出了文档d中出现单词w的概率。其中p(t|d)利用θd计算得到，p(w|t)利用φt计算得到。

实际上，利用当前的θd和φt，我们可以为一个文档中的一个单词计算它对应任意一个Topic时的p(w|d)，然后根据这些结果来更新这个词应该对应的topic。然后，如果这个更新改变了这个单词所对应的Topic，就会反过来影响θd和φt。

3.3 使用LDA生成主题特征，在之前特征的基础上加入主题特征进行文本分类

此处以cnews.test.txt文档为例，介绍LDA生成主题特征，进行文本分类的过程，demo如下(可见本节所有代码:戳链接)：

from nltk.stem.wordnet import WordNetLemmatizer
import gensim
from gensim import corpora
 
# 数据准备
# preprocess用于将一个文本文档进行切词，并以字符串形式输出切词结果
path = './cnews.test.txt'
with open(path,'r',encoding='UTF-8') as f:
    cnews_test = f.readlines()
# 取test中前3000出来分为2000为训练样本，1000测试样本
cnews_test = cnews_test[500:1000]+cnews_test[1500:2000]+cnews_test[2500:3000]+cnews_test[3500:4000]
# 将test中的label取出
test_label,test_x = [],[]
n = list(range(len(cnews_test)))
random.shuffle(n)
for i in n:
    each = cnews_test[i]
    each0 = each.split('\t')
    test_label.append(each0[0])
    test_x.append(each0[1])
    
# 载入停用词字典，对其进行去停用词
with open('./stopword.txt','r',encoding='UTF-8') as f:
    stopwords = f.readlines()
a = ''
for each in stopwords:
    a = a + ' '+each
stopwords = a.replace('\n','').split(' ')
stopwords = [each for each in stopwords if each not in ['\n','']]
 
test_x = [[each0 for each0 in jieba.cut(each) if each0 not in stopwords] for each in test_x] 
 
# 创建语料的词语词典，每个单独的词语都会被赋予一个索引
dictionary = corpora.Dictionary(test_x)
# 使用上面的词典，将转换文档列表（语料）变成 DT 矩阵
doc_term_matrix = [dictionary.doc2bow(doc) for doc in test_x]
 
#  使用 gensim 来创建 LDA 模型对象
Lda = gensim.models.ldamodel.LdaModel
# 在 DT 矩阵上运行和训练 LDA 模型
ldamodel = Lda(doc_term_matrix,num_topics=2,id2word=dictionary, passes=50)
# 输出结果
result_lda = ldamodel.print_topics(num_topics=2,num_words=20)
print(result_lda)

参考 https://blog.csdn.net/weixin_39441762/article/details/88356998
https://www.cnblogs.com/bentuwuying/p/6219970.html