【数据结构（C语言版）入门讲解】括号法建二叉树以及用括号法打印二叉树的逻辑讲解及代码实现

【数据结构（C语言版）入门讲解】括号法建二叉树以及用括号法打印二叉树的逻辑讲解及代码实现

---

开一个新的坑，用于讲解数据结构的基础知识。博主希望通过用最浅显易懂的文字来让更多人入门数据结构，让小白也能学会。今后也会补充栈、队列那些东西（希望我不会鸽太久），如果有机会也会开一个C语言入门讲解的坑（也希望我不会鸽太久）。博主能力也有限，如果有不恰当的地方或者错误的地方，敬请各位读者指正！

---

我们今天讨论两个问题：

1.如何用括号法建一个二叉树

2.如何把二叉树用括号法打印

---

首先，如何理解括号法？首先来看一个最简单的例子：

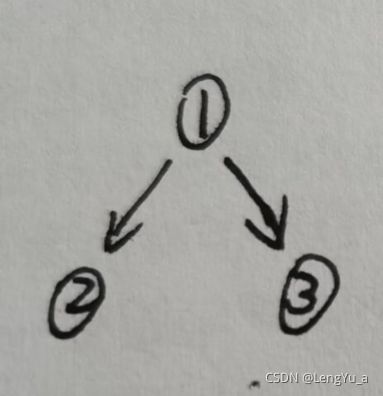
1(2,3)转换成二叉树：

很好理解建树的过程，也很好操作。现在加大一些难度，套一层括号：

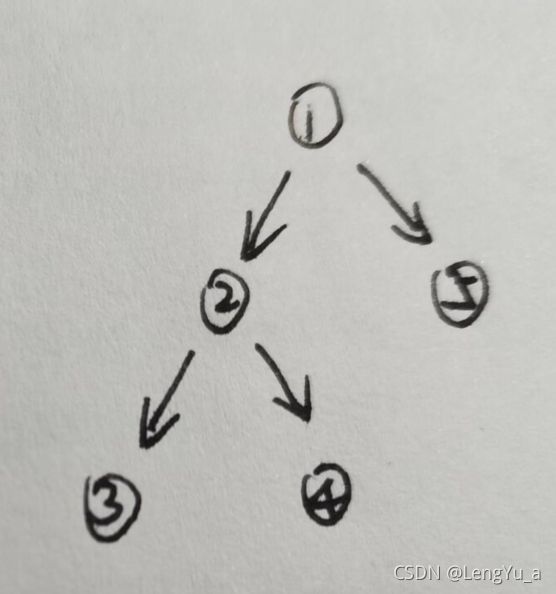
1(2(3,4),5)转换成二叉树：

回味一下这个过程，我们就会发现问题：我们都知道二叉树很容易通过“爹”找到两个孩子，但是无法通过孩子找到“爹”。这是由二叉树的结构决定的，二叉树的每一个结点都由数据域(data)，左孩子(*lchild)和右孩子(*rchild)组成，*lchild和*rchild都可以指向下一个data，但data只是一个元素，无法指回*lchild或*rchild。

理解二叉树这一性质后，我们再来看看刚刚第二个树，当我们建好“2”这个结点后，再建“3”这个结点，这时候我们好像就无法回到结点“2”了，因为我们没法通过结点“3”找到结点“2”，如果不能回到结点“2”，那我们也就无法再建结点“4”了。为解决这一问题，我们应该找一个东西，让它能暂存一下“2”这个结点。

再看一下刚刚的两棵树。

先看第一棵树：1(2,3)。建好结点“1”后，再建结点“2”，然后退回结点“1”，去建结点“3”；

再看第二棵树：1(2(3,4),5)。建好结点“1”后，建结点“2”，然后结点“3”，再退回到结点“2”，建结点“4”，再退回结点“1”，建结点“5”。

不难发现，如果我们括号的层数再多些，退回的次数还要更多，所以为了应对更复杂的情况，我们应该定义一组东西来暂存这些结点，而不是一个东西来暂存。

观察第二棵树，我们会先读取到结点“1”，再读取到结点“2”；在退回的时候，先退回到结点“2”，再退回到结点“1”——有点类似先进后出，后进先出。

结合这两个特点，不难联想到一个满足条件的东西——栈。

---

我们现在用栈再搞一下刚刚的两棵树。

1(2,3)

读到“1”：直接建个新的结点；

读到“(”：说明要处理左子树；同时我们要保存“1”结点，那么我们让结点“1”进栈；

读到“2”：建一个新的结点，然后读取栈中的“1”结点，连接到“2”结点，这时候就会发现一个“历史遗留问题”——计算机怎么知道是左还是右呢？

不出意外，我们应该还要引入一个变量用于区别左子树和右子树。不妨定义一个k，令k=1时处理左子树，k=2时处理右子树。现在我们重新看一下“(”那一步，我们加一条令k=1；那么在“2”这一步时就知道是处理左子树了。

读到“,”：这说明左子树已经处理完了，要处理右子树了，那么令k=2；

读到“3”：还是建一个新的结点，此时k=2，那么读取栈顶的“1”结点，把“1”和“3”连起来；

读到“)”：这一部分“()”已经读完了，让栈顶的“1”结点出栈。

那么1(2,3)这一棵最简单的二叉树已经讲解完了。

现在再玩一下第2棵树：

1(2(3,4),5)

读到“1”：直接建个新的结点；

读到“(”：结点“1”进栈，因为要处理左子树了，令k=1；

读到“2”：建个新的结点，读取栈顶结点“1”，此时k=1，则结点“2”为结点“1”的左孩子，连接起来；

读到“(”：结点“2”进栈，因为要处理左子树了，令k=1；

读到“3”：建个新的结点，读取栈顶结点“2”，此时k=1，则结点“3”为结点“2”的左孩子，连接起来；

读到“,”：要处理右子树了，令k=2；

读到“4”：建个新的结点，读取栈顶结点“2”，此时k=2，则结点“4”为结点“2”的右孩子，连接起来；

读到“)”：这一部分“()”已经读完了，让栈顶结点“2”出栈；

读到“,”：要处理右子树了，令k=2；

读到“5”：建个新的结点，读取栈顶结点“1”，此时k=1，则结点“5”为结点“1”的右孩子，连接起来；

读到“)”：这一部分“()”已经读完了，让栈顶结点“1”出栈。

那么1(2(3,4),5)这一棵树也就处理完了。

相信各位读者到现在已经大概明白了括号法建二叉树的手动操作过程，那我们再玩一棵更复杂的树来加深一下理解：

1(2(3,4),5(6(7,8),9(10,11)))

读到“1”：直接建个新的结点；

读到“(”：结点“1”进栈，因为要处理左子树了，令k=1；

读到“2”：建个新的结点，读取栈顶结点“1”，此时k=1，则结点“2”为结点“1”的左孩子，连接起来；

读到“(”：结点“2”进栈，因为要处理左子树了，令k=1；

读到“3”：建个新的结点，读取栈顶结点“2”，此时k=1，则结点“3”为结点“2”的左孩子，连接起来；

读到“,”：要处理右子树了，令k=2；

读到“4”：建个新的结点，读取栈顶结点“2”，此时k=2，则结点“4”为结点“2”的右孩子，连接起来；

读到“)”：这一部分“()”已经读完了，让栈顶结点“2”出栈；

读到“,”：要处理右子树了，令k=2；

读到“5”：建个新的结点，读取栈顶结点“1”，此时k=1，则结点“5”为结点“1”的右孩子，连接起来；

读到“(”：结点“5”进栈，因为要处理左子树了，令k=1；

读到“6”：建个新的结点，读取栈顶结点“5”，此时k=1，则结点“6”为结点“5”的左孩子，连接起来；

读到“(”：结点“6”进栈，因为要处理左子树了，令k=1；

读到“7”：建个新的结点，读取栈顶结点“6”，此时k=1，则结点“7”为结点“6”的左孩子，连接起来；

读到“,”：要处理右子树了，令k=2；

读到“8”：建个新的结点，读取栈顶结点“6”，此时k=2，则结点“8”为结点“6”的右孩子，连接起来；

读到“)”：这一部分“()”已经读完了，让栈顶结点“6”出栈；

读到“,”：要处理右子树了，令k=2；

读到“9”：建个新的结点，读取栈顶结点“5”，此时k=2，则结点“9”为结点“5”的右孩子，连接起来；

读到“(”：结点“9”进栈，因为要处理左子树了，令k=1；

读到“10”：建个新的结点，读取栈顶结点“9”，此时k=1，则结点“10”为结点“9”的左孩子，连接起来；

读到“,”：要处理右子树了，令k=2；

读到“11”：建个新的结点，读取栈顶结点“9”，此时k=2，则结点“11”为结点“9”的右孩子，连接起来；

读到“)”：这一部分“()”已经读完了，让栈顶结点“9”出栈；

读到“)”：这一部分“()”已经读完了，让栈顶结点“5”出栈；

读到“)”：这一部分“()”已经读完了，让栈顶结点“1”出栈。

那么1(2(3,4),5(6(7,8),9(10,11)))这一棵树也就处理完了。

需要注意的一点：存入到栈中的是结点！是结点！不是单单存入数据！单单存入数据是没有用的，存入结点才能找左孩子右孩子，才能连接起来二叉树。

相信到现在，各位读者已经完全理解用括号法建二叉树的过程了。在文章最后，我也贴上了我的代码，供各位参考。

---

用括号法打印二叉树就比建二叉树容易的多了。

请各位先手动操作一下，将上面1(2,3)和1(2(3,4),5)这两棵树玩一下。玩完之后，思考一个问题：我们为什么要加“()”？没错，是因为有孩子。为什么要加“,”？没错，是为了区分左右。我们很容易发现，我们的括号法打印二叉树的数据顺序与先序遍历顺序相同。那么我们只需要在先序遍历的基础上进行代码的修改即可，只需要在某些情况下打印“()”和“,”即可。

如果一个结点有孩子，那么就输出“(”；

如果结点有右孩子，那么输出“,”；

如果这一部分处理完，那么输出“)”。

其余的部分就是先序遍历的思想以及类似的代码了，在此不再多加讲解，以后如果有需求的话那么可以再单独讲一下二叉树的先序、中序和后序遍历。

---

下面是代码实现以及部分注释：

//21.11.18	1.0	括号法树的建立,用括号法打印树 
//21.11.18	1.1	完善了代码注释,整理了代码 


#include "stdio.h"
#include "malloc.h"


#define MaxLength 100							//二叉树括号写法的最大长度 
#define MaxSize 50								//临时栈的最大长度 


typedef char ElemType;							//由于要输入"("、")"、",",所以元素类型为char型 

typedef struct BTNode							//二叉树结点类型 
{
	ElemType data;									//数据域 
	struct BTNode *lchild;							//左孩子 
	struct BTNode *rchild;							//右孩子 
}BTreeNode;

typedef struct									//用于临时存放结点的栈 
{
	BTreeNode *node[MaxSize];						//结点是BTreeNode*类型的 
	int top;
}SqStack;


void StackInit(SqStack **s)						//栈初始化 
{
	(*s)=(SqStack *)malloc(sizeof(SqStack));
	(*s)->top=-1;
}

void StackDestroy(SqStack **s)					//销毁栈 
{
	free(*s);
}

void BTreeInit(BTreeNode **b)					//二叉树初始化 
{
	(*b)=(BTreeNode *)malloc(sizeof(BTreeNode));
	(*b)->lchild=NULL;								//定义一个指针,暂时不用的话令其值为NULL 
	(*b)->rchild=NULL;
}

void BTreeCreat1(BTreeNode **b)					//括号法建立二叉树 
{
	BTreeNode *t;									//用于建立新的结点 
	ElemType e;										//用于读取字符 
	ElemType elems[MaxLength];						//用于存放输入的字符串 
	SqStack *s;										//用于存放结点的栈 
	int k;											//用于标志处理左子树或右子树,k=1时处理左,k=2时处理右 
	int i;											//用于读取字符 
	
	t=NULL;
	i=0;
	
	StackInit(&s);									//初始化栈 
	
	printf("elems input:");
	gets(elems);									//读取输入的字符串 
	e=elems[i];										//读取第一个字符 
	
	while(e!='\0')
	{
		switch(e)
		{
			case '(':
				s->top++;
				s->node[s->top]=t;					//结点入栈 
				k=1;								//标志接下来处理左子树 
				break;
			case ')':
				s->top--;							//栈顶结点出栈 
				break;
			case ',':
				k=2;								//标志接下来处理右子树 
				break;
			default:
				BTreeInit(&t);						//建立新的结点 
				t->data=e;							//给data域赋值 
				if(i==0)							//i=0时说明这是第一个元素 
				{
					(*b)=t;							//和主函数中的b联系起来,这样就能修改二叉树的值了 
				}
				else
				{
					switch(k)
					{
						case 1:						//k=1时连接左子树 
							s->node[s->top]->lchild=t;
							break;
						case 2:						//k=2时连接右子树 
							s->node[s->top]->rchild=t;
							break;
					}
				}
		}
		i++;
		e=elems[i];									//读取下一个字符 
	}
	
	StackDestroy(&s);
}

/*
BTreeCreat2与BTreeCreat1实现原理完全相同,不再额外进行注释
区别:
BTreeCreat1是void类型,主函数给BTreeCreat1传双重指针
BTreeCreat2是BTreeNode*类型,主函数给BTreeCreat2传单重指针,该函数需要有返回值,将b返回到主函数中 
*/
/*
BTreeNode* BTreeCreat2(BTreeNode *b)			//括号法建二叉树
{
	BTreeNode *t;
	ElemType e;
	ElemType elems[MaxLength];
	SqStack *s;
	int k; 
	int i;
	
	t=NULL;
	i=0;
	
	StackInit(&s);
	
	printf("elems input:");
	gets(elems);
	printf("creat 1\n");
	e=elems[i];
	printf("creat 2\n");
	
	while(e!='\0')
	{
		switch(e)
		{
			case '(':
				s->top++;
				s->node[s->top]=t;
				k=1;
				break;
			case ')':
				s->top--;
				break;
			case ',':
				k=2;
				break;
			default:
				BTreeInit(&t);
				t->data=e;
				if(i==0)
				{
					b=t;
				}
				else
				{
					switch(k)
					{
						case 1:
							s->node[s->top]->lchild=t;
							break;
						case 2:
							s->node[s->top]->rchild=t;
							break;
					}
				}
		}
		i++;
		e=elems[i];
	}
	
	StackDestroy(&s);
	
	return b;
}
*/

void BTreePrint(BTreeNode *b)					//用括号法打印二叉树 
{
	if(b!=NULL)										//b非空 
	{
		printf("%c",b->data);
		if(b->lchild!=NULL||b->rchild!=NULL)		//有孩子才打印"()",没孩子不需要 
		{
			printf("(");
			BTreePrint(b->lchild);					//递归处理左孩子 
			if(b->rchild!=NULL)						//有右孩子才打印",",没有右孩子不需要 
			{
				printf(",");
			}
			BTreePrint(b->rchild);					//递归处理右孩子 
			printf(")");
		}
	}
}

void BTreeDestroy(BTreeNode **b)				//销毁二叉树 
{
	free(*b);
}


int main()
{
	BTreeNode *b;
	
	BTreeInit(&b);
	
	BTreeCreat1(&b);							//这两行代码请读者自取所需 
//	b=BTreeCreat2(b);
	
	BTreePrint(b);
	printf("\n");
	
	BTreeDestroy(&b);
	
	return 0;
}