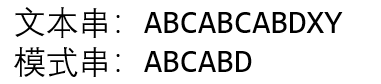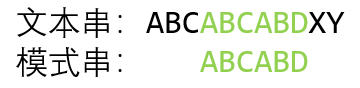[杂谈] 12. BF、KMP、RK Algorithm 字符串匹配算法
文章目录
-
-
- 0. 字符串匹配
- 1. BF 算法
-
- 1.1 算法由来
- 1.2 算法详解
- 1.3 BF 算法完整C++代码
- 2. KMP 算法
-
- 2.1 算法由来
- 2.2 算法详解
- 2.3 举个例子
- 2.4 next 数组
- 2.5 代码递推 next 数组
- 2.6 KMP 算法完整C++代码
- 3. RK 算法
-
- 3.1 算法由来
- 3.2 算法详解
- 3.3 RK 算法完整C++代码
-
0. 字符串匹配
字符串匹配就是在文本串 s 中查找模式串 t ,确定 t 是否为 s 的子串以及相关等效功能的过程。假设 s 中包含 m 个字符、t 中包含 n 个字符(m ≥ n)。
1. BF 算法
1.1 算法由来
BF算法,即暴风(Brute Force)算法,是普通的模式匹配算法,也是一种浅显易懂的暴力搜索算法。
1.2 算法详解
BF算法是一种暴力搜索算法,即逐一扫描 s[ i ],确定s[ i…i+n-1]是否与 t[ i…i+n-1]相同。
- 若相同, t 的所有字符一定扫描完,表示 t 是 s 的子串,返回 i (物理序号)或者 i + 1(逻辑序号)
- 若 s 的所有字符扫描完都没有相同的,表示 t 不为 s 的子串,返回 -1 (物理序号)或者0(逻辑序号)
1.3 BF 算法完整C++代码
#include BF 算法的最好情况时第一次匹配即成功,时间复杂度为O(n),最坏和平均时间复杂度都是O(m * n)。BF 算法尽管简单且效率低,但在编程中经常采用它来实现相关功能。
2. KMP 算法
2.1 算法由来
KMP算法,全称Knuth-Morris-Pratt算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。是一种字符串匹配的算法,用于在一个文本串S中查找模式串P的位置。 KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。
2.2 算法详解
该算法是 BF 算法的改进,提高了时间性能。那么是如何进行改进的呢?编程的基本思路是以空间换时间,保存一些加快匹配的信息。因为文本串每一趟都是从不同位置的字符开始比较的,而模式串会用于多次重复匹配,所以应该保持模式串的某些信息。
对于模式串 t,有用的信息是每个位置之前的最大前缀子串中字符的个数。所谓前缀,指若字符串 s1 是由另一个字符串 s2 的前面部分的连续字符组成的,则说 s1 是 s2 的前缀。例如:“ac” 是 “acm” 的前缀,“abc” 是 “abcd” 的前缀。前缀子串是指字符串 s 中某个子串是 s 的前缀,例如 “ababc” 中就有前缀子串 “ab”(即第二个"ab")。
在模式串 t 中每个位置都有这样的值,用 next 数组存放。例如, t = “abcabd”,约定 next[0] = -1, next [1] = 0;第 3 个字符 ‘c’ 前面的前缀子串为空,所以 next[2] = 0;第 4 个字符 ‘a’ 前面的前缀子串为空,所以 next[3] = 0;第 5 个字符 ‘b’ 前面的前缀子串为 “a”,所以 next[4] = 1;第 6 个字符 ‘d’ 前面的前缀子串为 “ab”,所以 next[5] = 2。这样的前缀子串可能有多个,用 next[j] 表示字符 t[j] 之前以 t[j - 1] 结尾的最大前缀子串中的字符个数。
那么最大前缀子串中字符的个数有什么用呢?下面看一个实例,若 s = “ABCABCABDXY”,t = “ABCABD”。
第一趟从 s[0] 和 t[0] 开始比较,直到 s[5] ≠ t[5](失配处),如果采用 BF 算法,第二趟从 s[1] 和 t[0] 开始比较,其实没有必要。因为对于 t ,有 next[5] = 2,说明有 “ t 0 t 1 t_0t_1 t0t1” = “ t 3 t 4 t_3t_4 t3t4”,而比较到 s 5 、 t 5 s_5、t_5 s5、t5才确定它们不相同,说明前面的字符是相同的,即有 " t 3 t 4 = s 3 s 4 t_3t_4=s_3s_4 t3t4=s3s4,从而有 " t 3 t 4 = t 0 t 1 t_3t_4=t_0t_1 t3t4=t0t1,如下图所示:
![[杂谈] 12. BF、KMP、RK Algorithm 字符串匹配算法_第1张图片](http://img.e-com-net.com/image/info8/e1bf1bc8f10a4984b4ad7a471d48a25a.jpg)
下一次应该是 s[5] 与 t[next[5]] (即next[2])比较(向右滑动 3 个字符),也就是从 s[2] 开始新的匹配 (不需要从 s[1]开始的那一趟),很快匹配成功。
注意: 这里将 next[0] 设置为 -1 ,即字符串的其实下标从 0 开始,如果规定字符串的其实下标从 1 开始,则约定 next[1] = 0, next[2] = 1,next[i] (i > 2)在上述计算结果的基础上加1。
KMP 算法消除了 BF 算法中的回溯,平均复杂度为O(m + n)
2.3 举个例子
经过上述 2.2 算法详解学习后,再次举个很普遍的例子,整体过一遍 KMP算法的流程:
假如有一个文本串 S 和一个模式串 P 如下:

出现 BF 算法第一次失配情况时一一即比较到模式串的D的位置,发现不匹配:
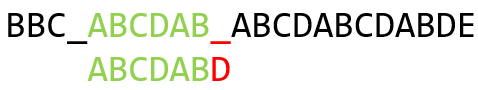
此时KMP算法并不是将模式串向右移动一位,而是向后移动四位,直接到这一步:

这样文本串的遍历位置并不会移回去,而是 ‘_’ 直接跟 ‘C’ 匹配。经过对 2.2 算法详解的学习,我们知道,移动位置实际上是 从 next 数组中查的值,再讲解 next 数组之前,先来讲一下 最大前缀后缀公共元素。
所谓最大前缀后缀公共元素,就是模式串中最大且相等的前缀和后缀,比如 aba ,有长度为 1 的相同前缀后缀 a ,再比如,字符串 acdac 有长度为 2 的相同前缀后缀 ac ,那么可以写出 ABCDABD 的每一位上的前缀后缀长度:
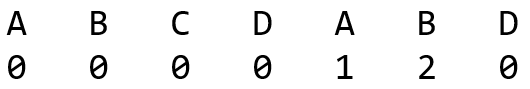
由于模式串的尾部可能有重复的字符,所以我们可以得出一个重要的结论:失配时,模式串向右移动的距离 = 已匹配字符数 - 失配字符的上一位字符所对应的最大长度值
之前是在字符 ’ D '处失配的,上一位字符是 ’ B ‘,对应的最大长度是2,此时已经成功匹配了 6 个字符,那么我们就将模式串向右移动 6 - 2 = 4位,并继续匹配即可。

此时发现 ’ _ ’ 和 ’ C ’ 不匹配,那么 ’ C ’ 的上一个字符 ’ B ’ 的最大长度为 0,此时已经匹配了 2 个字符,所以模式串向右移动 2 - 0 = 2 位继续匹配,得到:
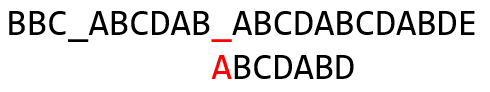
此时发现 ’ _ ’ 和 ’ A ’ 不匹配,’ A '已经是第一个了,不需要查表了,此时将模式串向右移动一位:
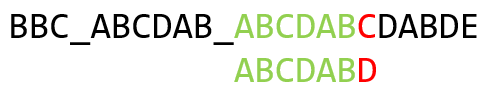
进行和之前相似的操作,上一位字符是 ’ B ',对应的最大长度是 2,此时已经成功匹配了 6 个字符,那么我们就将模式串向右移动 6 - 2 = 4 位,并继续匹配即可:

移动后发现模式串的首字母 ’ A '匹配上了,然后就按顺序一路往下匹配,最终完成模式串的匹配:
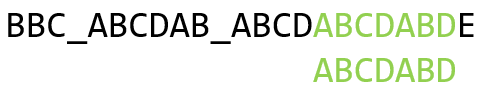
2.4 next 数组
经过上述步骤可以发现文本串中的遍历位置始终没有退后,一直都是在向前的,这样使得其比暴力破解法节省了大量的时间,其 时间复杂度为O(m+n),简直碉堡了。
读到这里是不是有疑问,怎么算法都结束了,还没next数组什么事呢,其实next数组和这里的最大前缀后缀公共元素长度数组是有关联的,上面的方法在失配时,要找失配字符前一个字符的最大前缀后缀公共元素长度值,那么如果将最大前缀后缀公共元素长度数组整体右移一位,形成next数组, 如下所示:
![[杂谈] 12. BF、KMP、RK Algorithm 字符串匹配算法_第2张图片](http://img.e-com-net.com/image/info8/9aa8415f88754b16b617e0291b592c4d.png)
上面的中间那行是之前的最大前缀后缀公共元素长度数组,我们将其整体右移一位,多出的位置补上一个-1,就变成了下面的一行。那么此时就直接找失配字符的next值就行了。于是就得到了新的结论:失配时,模式串向右移动的距离 = 失配字符所在位置 - 失配字符对应的next值。
2.5 代码递推 next 数组
在这来看看怎么利用代码来递推计算 next 数组。对于 next 的数组的计算,可以采用递推来算。根据上面的分析,知道如果模式串当前位置 j 之前有 k 个相同的前缀后缀,那么可以表示为 next[ j ] = k,所以如果当模式串的 p[ j ]跟文本串失配后,可以用 next[ j ]处的字符继续和文本串匹配,相当于模式串向右移动了 j - next[ j ]位。那么问题就来了,如何求出 next[ j + 1 ]的值呢,还是来看例子吧:
![[杂谈] 12. BF、KMP、RK Algorithm 字符串匹配算法_第3张图片](http://img.e-com-net.com/image/info8/6eece9c754054bc6ab8f62c6fb67c77c.jpg)
如上所示,模式串为 " ABCDABCE ",且 j = 6, k = 2,我们有 next[ j ] = k,这表示 j 位置上的字符 C 之前的最大前后缀长度为2,即 AB 。现在要求next[ j + 1 ]的值,因为 p[ k ] == p[ j ],所以 next[ j + 1] = next[ j ] + 1 = k + 1 = 3。即字母 E 之前的最大前后缀长度为 3,即ABC。
那么再来看 p[ k ] != p[ j ]的情况下怎么处理,还是来看例子:
![[杂谈] 12. BF、KMP、RK Algorithm 字符串匹配算法_第4张图片](http://img.e-com-net.com/image/info8/342f35568f27455e90571a603cb6d0f8.jpg)
这个例子把上面例子中的第二个 ’ C '换成了 ’ D ',所以字符 ’ E '前面的相同后缀就不再是3了,所以希望在k前面找出个k0位置,使得p[k0]为D,这样next[ j + 1] = k0 +1,但是这个例子中不存在这样的 ’ D ',所以next[j + 1] = 0。
来看一个能在前缀中找到 ’ D '的例子:
![[杂谈] 12. BF、KMP、RK Algorithm 字符串匹配算法_第5张图片](http://img.e-com-net.com/image/info8/fe37eeff9b0545869d5712d467e67ecd.jpg)
这个例子上面例子的最前面加上了个 ’ D ',此时 j = 7, k = 3了,有next[ j ] = k,这表示j位置上的字符 3 之前的最大前后缀长度为 3,即 DAB。要求next[ j + 1]的值,可以发现此时p[ k ] != p[ j ],然后让 k = next[ k ] = 0,此时p[ 0 ]是 D,那么 next[ j + 1] = k + 1 = 1了,这说明字母 E 之前的最大前后缀长度为 1,即 D。
综上所述,可以写出 next 的生成函数如下:
vector<int> getNext(string p) {
int n = p.size(), k = -1, j = 0;
vector<int> next(n, -1);
while (j < n - 1) {
if (k == -1 || p[j] == p[k]) {
++k; ++j;
next[j] = k;
} else {
k = next[k];
}
}
return next;
}
上面这种计算 next 数组的方式可以进一步的优化,可以优化的原因是因为上面的方法存在一个小小的问题,如果用这种方法求模式串ABAB,会得到next数组为[-1 0 0 1],用这个模式串去匹配 ABACABABC:

会发现 C 和 B 失配,那么根据上面的规则,要向右移动 j - next[ j ] = 3 - 1 = 2位,于是有:

右移两位后发现又是 C 和 B 失配了,而在上一步中,已知 p[ 3 ] = B, s[ 3 ] = C,就已经失配了,让 p[next[ 3 ]] = p[ 1 ] = B 再去和 s[ 3 ]比较,肯定还是失配。原因是当 p[ j ] != s[ i ]时,下一步要用 p[next[ j ]]和s[ i ]去匹配,而如果p[ j ] == p[next[ j ]]了,再用p[next[ j ]]和 s[ i ] 去匹配必然会失配。
所以要避免出现 p[ j ] == p[next[ j ]]的情况,一旦出现了这种情况,可以再次递归,next[ j ] = next[next[ j ]],修改后的代码如下:
vector<int> getNext(string p) {
int n = p.size(), k = -1, j = 0;
vector<int> next(n, -1);
while (j < n - 1) {
if (k == -1 || p[j] == p[k]) {
++k; ++j;
next[j] = (p[j] != p[k]) ? k : next[k];
} else {
k = next[k];
}
}
return next;
}
2.6 KMP 算法完整C++代码
#include 3. RK 算法
3.1 算法由来
RK 算法由 Rabin 和 Karp 提出。该算法最基本的思想为:Hash! 如果两个字符串 Hash 后的值不相同,则它们肯定不相同;如果它们 Hash 后的值相同,它们不一定相同。
3.2 算法详解
RK(Robin-Karp)算法也是对 BF 算法的一个改进,在 BF 算法中,每一个字符都需要进行比较,并且当发现首字符相同时,仍需要比较剩余的所有字符。在 RK 算法中,尝试只进行一次比较来判定两者是否相等。RK 算法的思路如下:
- 计算模式串 t 的 Hash(哈希)值
- 计算文本串 s 中每个长度为 n 的子串的 Hash值(共需要计算 m - n + 1次)
- 从 s 的第 1 个长度为 n 的子串开始,与模式串 t 的 Hash 值进行比较,如果 Hash 值不同,进入下一趟匹配;如果 Hash 值相同,再对两者调用 BF 算法进行判断。
例如:s = “abcdefg”,t = “def”。RK 算法先计算 t 的 Hash 值为 H t H_t Ht。再分别计算 “abc”、“bcd”、“cde”、"def"的 Hash 值 H a 、 H b 、 H c 、 H d ( H d = H t ) H_a、H_b、H_c、H_d(H_d = H_t) Ha、Hb、Hc、Hd(Hd=Ht)。t 分别与 “abc”、“bcd”、“cde” 比较,它们的 Hash 值不相等,再与 “def” 的 Hash 值比较,两者相等,继续调用 BF 算法得出是相同的表示 t 是 s 的子串。
RK 算法的时间复杂度为 O(m * n),但在实际应用中往往比较快,期望时间为O(m +n),
RK 算法相较于 KMP 算法时间稍慢的原因主要有两点,一是数学取模运算,二是 Hash 结果相同不一定完全匹配,需要再逐字符进行对比。即主要针对以下两点进行优化:
- 一是用其他运算代替取模运算
- 二是降低 Hash 冲突
经过优化后,RK 算法在长字符串匹配效率上已优于一般的 KMP 算法。详情请移步dalao博文:独树一帜的字符串匹配算法——RK算法
3.3 RK 算法完整C++代码
#include