python数据降维

1.数据为何要降维

• 降低模型的计算量，减少模型运行时间，减少数据存储空间；
• 降低噪音变量信息对于模型结果的影响；
• 它通过删除冗余的特征来处理多重共线性问题。例如，你有两个变量 - “在跑步机上花费的时间”和“燃烧的卡路里”。这些变量是高度相关的，因为你在跑步机上花费的时间越多，你燃烧的卡路里就越多。因此，存储两个变量都没有意义，只有其中一个可以满足需求；
• 较简单的模型在小数据集有更强的鲁棒性；
• 当数据能用较少的特征进行解释，我们可以更好的解释数据，使得我们可以提取知识；
• 便于通过可视化方式展示归约后的维度信息。

因此，大多数情况下，当我们面临高维数据时，都需要对数据做降维处理。

数据降维有两种方式：特征选择，维度转换

特征选择

特征选择指根据一定的规则和经验，直接在原有的维度中挑选一部分参与到计算和建模过程，用选择的特征代替所有特征，不改变原有特征，也不产生新的特征值。
特征选择的降维方式好处是可以保留原有维度特征的基础上进行降维，既能满足后续数据处理和建模需求，又能保留维度原本的业务含义，以便于业务理解和应用。对于业务分析性的应用而言，模型的可理解性和可用性很多时候要有限于模型本身的准确率、效率等技术指标。例如，决策树得到的特征规则，可以作为选择用户样本的基础条件，而这些特征规则便是基于输入的维度产生。

维度转换

这个是按照一定数学变换方法，把给定的一组相关变量（维度）通过数学模型将高纬度空间的数据点映射到低纬度空间中，然后利用映射后变量的特征来表示原有变量的总体特征。这种方式是一种产生新维度的过程，转换后的维度并非原来特征，而是之前特征的转化后的表达式，新的特征丢失了原有数据的业务含义。 通过数据维度变换的降维方法是非常重要的降维方法，这种降维方法分为线性降维和非线性降维两种，其中常用的代表算法包括独立成分分析（ICA），主成分分析（PCA），因子分析（Factor Analysis，FA），线性判别分析（LDA），局部线性嵌入（LLE），核主成分分析（Kernel PCA）等。

2.常用的降维技术

2.1缺失值比率 (Missing Values Ratio)

假设你有一个数据集。你的第一步是什么？在构建模型之前，你应该会希望先探索数据。在研究数据时，你会发现数据集中存在一些缺失值。怎么办？你将尝试找出这些缺失值的原因，然后将输入它们或完全删除具有缺失值的变量（使用适当的方法）。

如果我们有太多的缺失值（比如说超过50％）怎么办？我们应该输入这些缺失值还是直接删除变量？我宁愿放弃变量，因为它没有太多的信息。然而，这不是一成不变的。我们可以设置一个阈值，如果任何变量中缺失值的百分比大于该阈值，我们将删除该变量。

我们将使用一个实践问题：Big Mart Sales III中的数据集。其中，Item_Outlet_Sales折扣店销量为因变量。

我们将检查每个变量中缺失值的百分比。我们可以使用.isnull（）.sum（）来计算它。

检查每个变量中缺失值的百分比
train.isnull().sum()/len(train)*100

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
train=pd.read_csv("Train_UWu5bXk.csv")
print(train.isnull().sum()/len(train)*100)

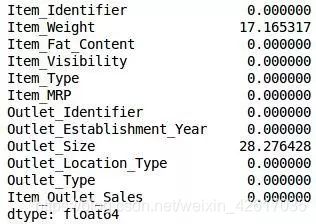
正如你在上表中所看到的，并没有太多的缺失值（实际上只有2个变量具有缺失值）。我们可以使用适当的方法来输入变量，或者我们可以设置阈值，比如20％，并删除具有超过20％缺失值的变量。让我们看看如何在Python中完成此操作：
保存变量中缺失的值

a = train.isnull().sum()/len(train)*100

将列名保存在变量中

variables = train.columns
variable = [ ]
for i in range(0,12):
    if a[i]<=20: #将阈值设置为20%
        variable.append(variables[i])
print(variable)

因此，要使用的变量存储在“variables”中，它只包含哪些缺失值小于20%的特征。

2.2低方差过滤器(Low Variance Filter)

与缺失值比率进行数据降维方法相似，该方法假设数据列变化非常小的列包含的信息量少。因此，所有的数据列方差小的列被移除。需要注意的一点是：方差与数据范围相关的，因此在采用该方法前需要对数据做归一化处理。

假设我们的数据集中的一个变量，其中所有观察值都是相同的，例如1。如果我们要使用此变量，你认为它可以改进我们将要建立的模型么？答案当然是否定的，因为这个变量的方差为零。

因此，我们需要计算给出的每个变量的方差。然后删除与我们的数据集中其他变量相比方差比较小的变量。如上所述，这样做的原因是方差较小的变量不会影响目标变量。

让我们首先使用已知ItemWeight观察值的中值来填充temWeight列中的缺失值。对于OutletSize列，我们将使用已知OutletSize值的模式来填充缺失值：

train[‘Item_Weight’].fillna(train[‘Item_Weight’].median(), inplace=True)
train[‘Outlet_Size’].fillna(train[‘Outlet_Size’].mode()[0], inplace=True)

让我们检查一下是否所有的缺失值都已经被填满了：

train.isnull().sum()/len(train)*100

#使用已知OutletSize值的模式来填充缺失值
train['Item_Weight'].fillna(train['Item_Weight'].median(), inplace=True)
train['Outlet_Size'].fillna(train['Outlet_Size'].mode()[0], inplace=True)
#检查一下是否所有的缺失值都已经被填满了：
print(train.isnull().sum()/len(train)*100)

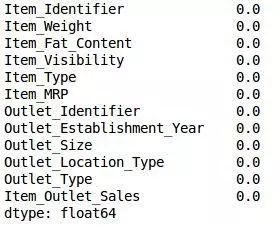
嘿瞧！我们都已经准备好了。现在让我们计算所有数值变量的方差。

train.var()

如上面的输出所示，与其他变量相比，Item_Visibility的方差非常小。我们可以安全地删除此列。这就是我们应用低方差过滤器的方法。让我们在Python中实现这个：

#Item_Visibility的方差非常小,删除此列：
numeric = train[['Item_Weight', 'Item_Visibility', 'Item_MRP', 'Outlet_Establishment_Year']]
var = numeric.var()
numeric = numeric.columns
variable = [ ]
for i in range(0,len(var)):
    if var[i]>=10: #将阈值设置为10%
        variable.append(numeric[i])
print(variable)

上面的代码为我们提供了方差大于10的变量列表。

['Item_Weight', 'Item_MRP', 'Outlet_Establishment_Year']

2.3高相关过滤器 (High Correlation Filter)

高相关滤波认为当两列数据变化趋势相似时，它们包含的信息也相似。这样，使用相似列中的一列就可以满足机器学习模型。对于数值列之间的相似性通过计算相关系数来表示，对于数据类型为类别型的相关系数可以通过计算皮尔逊卡方值来表示。相关系数大于某个阈值的两列只保留一列。同样要注意的是：相关系数对范围敏感，所以在计算之前也需要对数据进行归一化处理。

两个变量之间的高度相关意味着它们具有相似的趋势，并且可能携带类似的信息。这可以大大降低某些模型的性能（例如线性回归和逻辑回归模型）。我们可以计算出本质上是数值的独立数值变量之间的相关性。如果相关系数超过某个阈值，我们可以删除其中一个变量（丢弃一个变量是非常主观的，并且应该始终记住该变量）。

作为一般准则，我们应该保留那些与目标变量显示出良好或高相关性的变量。

让我们在Python中执行相关计算。我们将首先删除因变量（ItemOutletSales）并将剩余的变量保存在新的DataFrame（df）中。

df=train.drop(‘Item_Outlet_Sales’, 1)
df.corr()

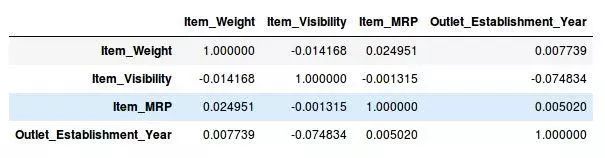
太棒了，我们的数据集中没有任何具有高相关性的变量。通常，如果一对变量之间的相关性大于0.5-0.6，我们真的应该认真的考虑丢弃其中的一个变量。

2.4 随机森林 (Random Forests)

组合决策树通常又被成为随机森林，它在进行特征选择与构建有效的分类器时非常有用。一种常用的降维方法是对目标属性产生许多巨大的树，然后根据对每个属性的统计结果找到信息量最大的特征子集。例如，我们能够对一个非常巨大的数据集生成层次非常浅的树，每颗树只训练一小部分属性。如果一个属性经常成为最佳分裂属性，那么它很有可能是需要保留的信息特征。对随机森林数据属性的统计评分会向我们揭示与其它属性相比，哪个属性才是预测能力最好的属性。

随机森林是最广泛使用的特征选择算法之一。它附带内置的重要功能，因此你无需单独编程。这有助于我们选择较小的特征子集。

我们需要通过应用一个热编码将数据转换为数字形式，因为随机森林（Scikit-Learn实现）仅采用数字输入。让我们也删除ID变量（Item_Identifier和Outlet_Identifier），因为这些只是唯一的数字，目前对我们来说并不重要。

from sklearn.ensemble import RandomForestRegressor
df=df.drop(['Item_Identifier', 'Outlet_Identifier'], axis=1)
model = RandomForestRegressor(random_state=1, max_depth=10)
df=pd.get_dummies(df)
model.fit(df,train.Item_Outlet_Sales)
#拟合模型后，绘制特征重要性图：
features = df.columns
importances = model.feature_importances_
indices = np.argsort(importances)[-9:] # top 10 features
plt.title('Feature Importances')
plt.barh(range(len(indices)), importances[indices], color='b', align='center')
plt.yticks(range(len(indices)), [features[i] for i in indices])
plt.xlabel('Relative Importance')
plt.show()

基于上图，我们可以手动选择最顶层的特征来减少数据集中的维度。值得注意的是，我们可以使用sklearn的SelectFromModel来实现这一点。它根据权重的重要性来选择特征。

——————————————————————————————

到目前为止我们看到的技术通常在我们的数据集中没有太多变量时使用。这些或多或少的特征选择技术，在接下来的部分中，我们将使用Fashion MNIST数据集，该数据集包含属于不同类型服装的图像，例如T恤，裤子，包等。数据集可点击此处下载，提取码为：a708。

该数据集共有70,000张图像，其中60,000张在训练集中，其余10,000张是测试图像。在本文的范围中，我们将仅处理训练图像。训练集文件采用zip格式。解压缩zip文件后，你将获得一个.csv文件和一个包含这60,000张图像的训练集文件夹。每个图像的相应标签可以在’train.csv’文件中找到。

2.5 因子分析（FA）

通过研究众多变量之间的内部依赖关系，探求观测数据中的基本结构，并用少数几个假想变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。原始的变量是可观测的显在变量，而假想变量是不可观测的潜在变量，称为因子。

因子分析又存在两个方向，一个是探索性因子分析。另一个是验证性因子分析。探索性因子分析是不确定一堆自变量背后有几个因子，我们通过这种方法试图寻找到这几个因子。而验证性因子分析是已经假设自变量背后有几个因子，试图通过这种方法去验证一下这种假设是否正确。验证性因子分析又和结构方程模型有很大关系。

假设我们有两个变量：收入和教育。这些变量可能具有高度相关性，因为具有较高教育水平的人往往具有显着较高的收入，反之亦然。

在因子分析技术中，变量按其相关性进行分组，即特定组内的所有变量之间具有高度相关性，但往往与其他组的变量之间相关性较低。在这里，每个组都被称为一个因子。与原始数据维度相比，这些因子的数量很少。但是，这些因子往往很难观察到。

让我们先读入训练集文件夹中包含的所有图像：

import pandas as pd
import numpy as np
from glob import glob
import cv2 #pip install opencv-python
images = [cv2.imread(file) for file in glob(‘train/*.png’)]

注意：你必须使用train文件夹的路径替换glob函数内的路径。

现在我们将这些图像转换为 numpy数组格式，以便我们可以执行数学运算并绘制图像。

images = np.array(images)
images.shape

（60000,28,28,3）

如上所示，它是一个三维数组。我们必须将它转换为一维的，因为所有即将出现的技术只需要一维输入。为此，我们需要展平图像：

image = []
for i in range(0,60000):
img = images[i].flatten()
image.append(img)
image = np.array(image)

现在让我们创建一个DataFrame，其中包含每个图像中每个像素的像素值，以及它们对应的标签（对于标签，我们将使用train.csv文件）。

train = pd.read_csv(“train.csv”) # 给出你的train.csv文件的完整路径
feat_cols = [ ‘pixel’+str(i) for i in range(image.shape[1]) ]
df = pd.DataFrame(image,columns=feat_cols)
df[‘label’] = train[‘label’]

现在我们将使用因子分析来分解数据集：

from sklearn.decomposition import FactorAnalysis
FA = FactorAnalysis(n_components = 3).fit_transform(df[feat_cols].values)

这里，n_components将决定转换数据中的因子数量。转换数据后，是时候可视化结果了：

import matplotlib.pyplot as plt
plt.figure(figsize=(12,8))
plt.title(‘Factor Analysis Components’)
plt.scatter(FA[:,0], FA[:,1])
plt.scatter(FA[:,1], FA[:,2])
plt.scatter(FA[:,2],FA[:,0])
plt.show()

'''因子分析（FA）'''
import pandas as pd
import numpy as np
from glob import glob
import cv2  #pip install opencv-python
images = [cv2.imread(file) for file in glob('./Fashion MNIST/traintemp/traintemp/*.png')]
#将这些图像转换为 numpy数组格式，以便我们可以执行数学运算并绘制图像。
images = np.array(images)
print(images.shape)

#可见它是一个三维数组。必须将它转换为一维的，需要展平图像
image = []
for i in range(0,600):
    img = images[i].flatten()
    image.append(img)
image = np.array(image)

#创建一个DataFrame，其中包含每个图像中每个像素的像素值，以及它们对应的标签
# 对于标签，我们将使用train.csv文件
train = pd.read_csv("./Fashion MNIST/traintemp/train.csv")
feat_cols = [ 'pixel'+str(i) for i in range(image.shape[1]) ]
df = pd.DataFrame(image,columns=feat_cols)
df['label'] = train['label']

#使用因子分析来分解数据集
from sklearn.decomposition import FactorAnalysis
FA = FactorAnalysis(n_components = 3).fit_transform(df[feat_cols].values)

#这里，n_components将决定转换数据中的因子数量。转换数据后，可视化结果：
import matplotlib.pyplot as plt
plt.figure(figsize=(12,8))
plt.title('Factor Analysis Components')
plt.scatter(FA[:,0], FA[:,1])
plt.scatter(FA[:,1], FA[:,2])
plt.scatter(FA[:,2],FA[:,0])
plt.show()

2.6 主成分分析 (PCA)

主成分分析是一个统计过程，该过程通过正交变换将原始的 n 维数据集变换到一个新的被称做主成分的数据集中。变换后的结果中，第一个主成分具有最大的方差值，每个后续的成分在与前述主成分正交条件限制下具有最大方差。降维时仅保存前 m(m < n) 个主成分即可保持最大的数据信息量。

主要思想：

把数据从原来的坐标系转换到新的坐标系，新坐标系的选择由数据本身决定：第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴选择和第一个坐标轴正交且具有方差次大的方向。此过程一直重复，重复次数为原始数据中特征的数目。大部分方差都集中在最前面的几个新坐标轴中。因此，可以忽略剩下的坐标轴，即对数据进行了降维处理。

注意：

主成分变换对正交向量的尺度敏感。数据在变换前需要进行归一化处理。
新的主成分并不是由实际系统产生的，因此在进行 PCA 变换后会丧失数据的解释性。如果说，数据的解释能力对你的分析来说很重要，那么 PCA 对你来说可能就不适用了。

在继续之前，我们将从我们的数据集中随机绘制一些图像：

#从我们的数据集中随机绘制一些图像
rndperm = np.random.permutation(df.shape[0])
plt.gray()
fig = plt.figure(figsize=(20,10))
for i in range(0,15):
    ax = fig.add_subplot(3,5,i+1)
    ax.matshow(df.loc[rndperm[i],feat_cols].values.reshape((28,28*3)).astype(float))
plt.show()

让我们使用Python实现PCA降维并转换数据集：

from sklearn.decomposition import PCA
pca = PCA(n_components=4)
pca_result = pca.fit_transform(df[feat_cols].values)

在这种情况下，n_components将决定转换数据中的主要成分的数量。让我们看一下使用这4个成分解释了多少差异。我们将使用explainvarianceratio_来计算相同的内容。

plt.plot(range(4), pca.explained_variance_ratio_)
plt.plot(range(4), np.cumsum(pca.explained_variance_ratio_))
plt.title(“Component-wise and Cumulative Explained Variance”)
plt.show()

在上图中，蓝线表示按成分解释的方差，而橙线表示累积解释的方差。我们只用四个组件就可以解释数据集中大约60％的方差变化。现在让我们尝试可视化每个分解的成分：

#在上图中，蓝线表示按成分解释的方差，而橙线表示累积解释的方差。
# 我们只用四个组件就可以解释数据集中大约60％的方差变化。
# 现在让我们尝试可视化每个分解的成分：
import seaborn as sns
plt.style.use('fivethirtyeight')
fig, axarr = plt.subplots(2, 2, figsize=(12, 8))
sns.heatmap(pca.components_[0, :].reshape(28, 84), ax=axarr[0][0], cmap='gray_r')
sns.heatmap(pca.components_[1, :].reshape(28, 84), ax=axarr[0][1], cmap='gray_r')
sns.heatmap(pca.components_[2, :].reshape(28, 84), ax=axarr[1][0], cmap='gray_r')
sns.heatmap(pca.components_[3, :].reshape(28, 84), ax=axarr[1][1], cmap='gray_r')
axarr[0][0].set_title("{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[0]*100), fontsize=12)
axarr[0][1].set_title("{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[1]*100), fontsize=12)
axarr[1][0].set_title("{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[2]*100), fontsize=12)
axarr[1][1].set_title("{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[3]*100), fontsize=12)
axarr[0][0].set_aspect('equal')
axarr[0][1].set_aspect('equal')
axarr[1][0].set_aspect('equal')
axarr[1][1].set_aspect('equal')

plt.suptitle('4-Component PCA')
plt.show()

我们添加到PCA技术中的每个额外维度获取模型中的方差越来越少。第一个部分是最重要的成分，其次是第二个成分，然后是第三个成分，依此类推。

完整代码

'''PCA'''
#从我们的数据集中随机绘制一些图像
rndperm = np.random.permutation(df.shape[0])
plt.gray()
fig = plt.figure(figsize=(20,10))
for i in range(0,15):
    ax = fig.add_subplot(3,5,i+1)
    ax.matshow(df.loc[rndperm[i],feat_cols].values.reshape((28,28*3)).astype(float))
plt.show()

#PCA降维并转换数据集
from sklearn.decomposition import PCA
pca = PCA(n_components=4)
pca_result = pca.fit_transform(df[feat_cols].values)
#n_components将决定转换数据中的主要成分的数量。
# 看看使用这4个成分解释了多少差异。我们将使用explainvarianceratio_来计算相同的内容。
plt.plot(range(4), pca.explained_variance_ratio_)
plt.plot(range(4), np.cumsum(pca.explained_variance_ratio_))
plt.title("Component-wise and Cumulative Explained Variance")
plt.show()

#在上图中，蓝线表示按成分解释的方差，而橙线表示累积解释的方差。
# 我们只用四个组件就可以解释数据集中大约60％的方差变化。
# 现在让我们尝试可视化每个分解的成分：
import seaborn as sns
plt.style.use('fivethirtyeight')
fig, axarr = plt.subplots(2, 2, figsize=(12, 8))
sns.heatmap(pca.components_[0, :].reshape(28, 84), ax=axarr[0][0], cmap='gray_r')
sns.heatmap(pca.components_[1, :].reshape(28, 84), ax=axarr[0][1], cmap='gray_r')
sns.heatmap(pca.components_[2, :].reshape(28, 84), ax=axarr[1][0], cmap='gray_r')
sns.heatmap(pca.components_[3, :].reshape(28, 84), ax=axarr[1][1], cmap='gray_r')
axarr[0][0].set_title("{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[0]*100), fontsize=12)
axarr[0][1].set_title("{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[1]*100), fontsize=12)
axarr[1][0].set_title("{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[2]*100), fontsize=12)
axarr[1][1].set_title("{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[3]*100), fontsize=12)
axarr[0][0].set_aspect('equal')
axarr[0][1].set_aspect('equal')
axarr[1][0].set_aspect('equal')
axarr[1][1].set_aspect('equal')

plt.suptitle('4-Component PCA')
plt.show()

我们还可以使用奇异值分解 （SVD）将我们的原始数据集分解为其成分，从而减少维数。

SVD将原始变量分解为三个组成矩阵。它主要用于从数据集中删除冗余的特征。它使用特征值和特征向量的概念来确定这三个矩阵。由于本文的范围，我们不会深入研究它的理论，但让我们坚持我们的计划，即减少数据集中的维度。

让我们实现SVD并分解我们的原始变量：

from sklearn.decomposition import TruncatedSVD
svd = TruncatedSVD(n_components=3, random_state=42).fit_transform(df[feat_cols].values)

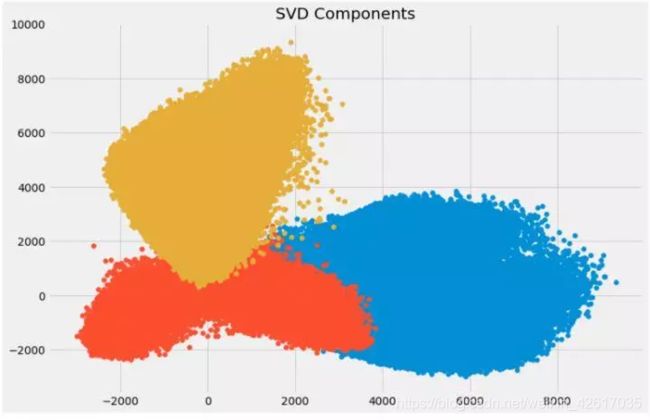
让我们通过绘制前两个主成分来可视化变换后的变量：

plt.figure(figsize=(12,8))
plt.title('SVD Components')
plt.scatter(svd[:,0], svd[:,1])
plt.scatter(svd[:,1], svd[:,2])
plt.scatter(svd[:,2],svd[:,0])
plt.show()