【去噪】A Physics-Based Noise Formation Model for Extreme Low-Light Raw Denoising噪声建模详解

0. 前言

一句话总结：使用改论文提出的噪声生成模型合成数据所训练出的模型，其网络去噪能力可以媲美用大量配对数据训练的模型，避免费时费力地采集大量真实配对数据。

1. 主要贡献

1.1 建立了一个全面的噪声模型，可以准确地描述低光环境下的真实噪声结构

数字传感器原始图像D的创建通常可以用一个线性模型来表示：


式中，$I$为与场景辐照成比例的光电子数，$K$表示由模拟和数字增益组成的整体系统增益，$N$表示所有噪声源之和。
根据成像pipline，可以将成像过程分为三个阶段：
（1）光子到电子
在曝光过程中，入射光以光子形式击中光传感器像素区域，释放出与光强成正比的光电子。由于光的量子性质，所收集的电子的数量不可避免地存在不确定性，这种不确定性对电子数量施加了泊松分布。

在光子到电子阶段还引入了其他一些噪声源，如光响应不均匀性和暗电流噪声。由于CMOS传感器设计和制造的技术进步，如传感器上的暗电流抑制，导致新一代数字单反相机具有较低的暗电流和更好的光响应均匀性。因此，可以假设一个恒定的光响应，并将暗电流噪声$N_d$的影响划分到读出噪声$N_{read}$。

（2）电子到电压
① 读出噪声
当电子在光传感器的每个像素位置被收集到后，它们通常被整合、放大，并在曝光时间结束时读出为可测量的电荷或电压。在电子到电压阶段出现的噪声取决于所使用的电路设计和处理技术，因此被称为像素电路噪声，包括热噪声、复位噪声、源跟随器噪声和条带模式噪声。在模型中考虑了热噪声$N_t$、源跟随器噪声$N_s$和带型噪声$N_b$。为了简化分析，将暗电流噪声$N_d$、热噪声$N_t$和源跟随器噪声$N_s$统称为读出噪声；带型噪声$N_b$单独考虑。

读出噪声通常假设遵循高斯分布，但噪声数据的分析显示其形状的长尾性质。这可以归因于源跟随器噪声的闪烁和随机电报信号分量，或由暗电流引起的暗峰值。因此，使用一个可以更好地描述长尾形状的统计分布–Tukey-lambda分布来建模读出噪声。

其中，$\lambda$ 和 ${\sigma }_{TL}$分别表示形状和尺度参数。

② 颜色偏差读噪声
虽然零平均噪声假设在大多数情况下普遍适用，但在极低光设置下会失效，因为不可忽略的直流电噪声分量。这个分量来源于暗电流噪声，这使得噪声分布不再为零中心。虽然暗电流噪声已经被现代传感器暗电流抑制技术大大消除，但由于应用系统增益K来放大信号和噪声，剩余分量仍然有影响。评估显示直流噪声成分在不同颜色通道中是变化的，这种颜色不均匀的直流分量是导致在极低照度下经常观察到的颜色偏差现象的罪魁祸首。为了使噪声模型简单而紧凑，将直流噪声分量（即颜色偏差）建模为读取噪声模型的平均值：

③ 行噪声
Nb图像中可能在以水平或垂直线的形式出现，通过对偏置帧进行离散傅里叶变换，可以测试条带型噪声。中心化的傅里叶光谱中突出显示的垂直模式揭示了行噪声分量的存在。因此模型中只考虑行分量（水平条纹），列分量可以忽略不计。

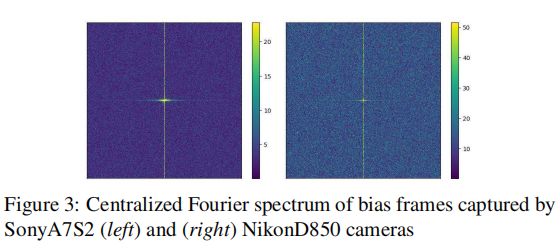
对于每一行，通过从零均值高斯分布N（0，σr）中采样一个值来模拟Nr，然后将其作为偏移量添加到该行中的所有像素中。

（3）电压到数字信号
为了生成可以存储在数字存储介质中的图像，通过模数转换器将读出的模拟电压信号量化为数字信号值，在此过程中会引入量化误差。量化噪声Nq是模拟电压和数字值之间的舍入误差，假定其遵循均匀分布。

q为数字信号的位数。

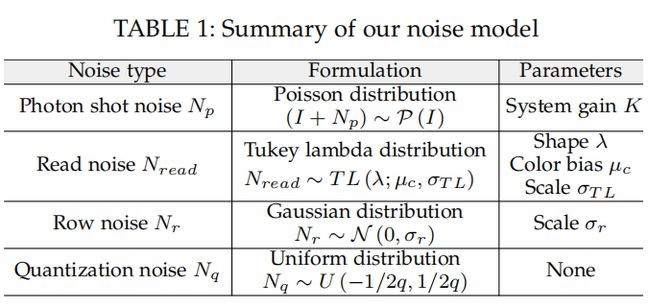
1.2 提出了一种噪声参数标定方法

对于建立的噪声模型，需要标定的参数如下：

标定方法利用了在特殊设置下捕获的两种原始图像，即平场帧和偏置帧来估计噪声参数。平场帧是当传感器被均匀照明时所捕获的图像。将一张白纸固定在灯光均匀的墙上，相机被安装在靠近纸张的三脚架上，镜头聚焦在无穷远处以减少不均匀性。偏置帧是指在无光照环境下曝光时间最短的图像，在黑暗的房间中拍摄，并且要将相机的镜头盖上。
平场帧表征了与光相关的光子散粒噪声，因此可以用来估计相关参数K，而偏置帧表示不依赖于光的暗噪声图像，可以用来依次推导出其他噪声参数${\mu }_c$、${\sigma }_r$、$\lambda$、${\sigma }_{TL}$。

1.2.1 估计系统总体增益 $K$

根据以上推算，原始噪声图像的方差与真实信号值呈线性关系，通过最小二乘拟合一下，斜率即为系统总体增益K，真实信号KI使用平场帧的中值近似代替。

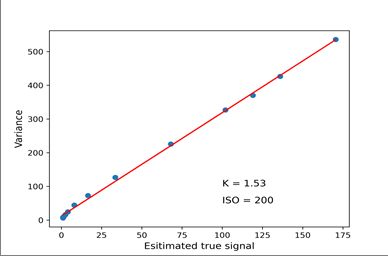
给定估计的K，我们可以首先将原始光电子信号D转换为光电子数I，然后对其施加泊松分布，最后将其恢复为泊松分布，从而模拟真实的光子发射噪声。

1.2.2 估计颜色偏差噪声的${\mu }_c$

给定一个偏置帧，可以通过平均偏置帧的每个颜色通道内的所有像素值来检查直流噪声分量。如果噪声分布没有直流分量，为零中心，得到的颜色值应该几乎等于原始图像元数据中记录的黑电平（每个通道）。
作者发现这些值严重偏向于记录的黑色水平，这不能解释为由其他零平均噪声引起的随机波动，而是揭示了直流噪声分量的存在。下图展示了从多个偏差帧计算出的每个颜色通道的偏差µc的密度直方图。在颜色通道之间的直方图上有明显的差异，这表明在颜色通道上直流噪声分量的统计量不同。

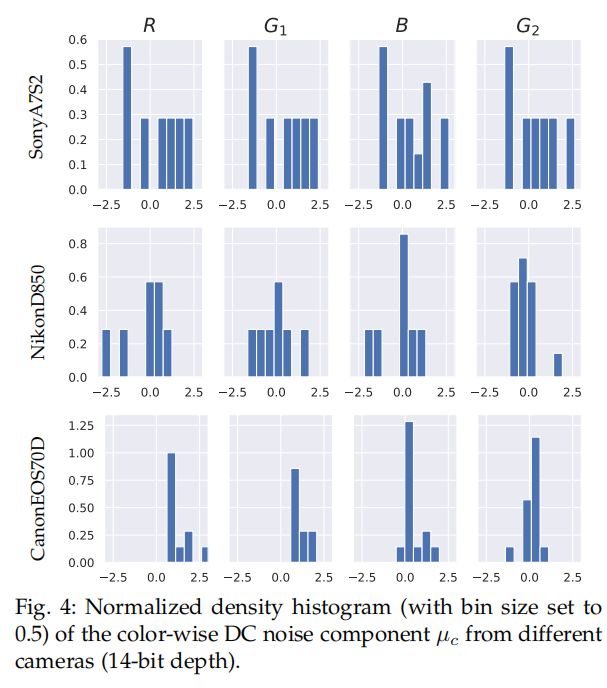
基于这一观察结果，在建立的噪声模型中考虑到了颜色偏差噪声，这对于极低光去噪非常重要，因为由于信号和噪声的大数字增益（如×100），小的偏置可能在极低光中导致严重的颜色偏移。
为了排除直流噪声对其他噪声成分的影响，在估计其他噪声参数之前需要从偏置帧中减去每个颜色通道的平均值。

1.2.3 估计行噪声的σr

每个通道减去颜色偏差后，统计图像每一行的均值得到X；通过正态概率图和Shapiro-Wilk test检验其是否服从正态分布，若服从，通过最大化对数似然值估计出尺度参数sigma_r。

Shapiro-Wilk test：stats.shapiro，所得到的p值高于0.05，说明不能拒绝数据为正态分布的零假设。
正态概率图：stats.probplot
估计sigma_r：stats.norm.fit

1.2.4 估计读出噪声中的λ、σT L

先从偏置帧中减去颜色偏差，再去除估计的行噪声，得到data
通过lambda = scipy.stats.ppcc_max(data, dist=‘tukeylambda’)计算$\lambda$参数
通过scipy.stats.ppcc_plot(raw_in, a=lambda/2, b=2*lambda, dist=‘tukeylambda’, plot=ax)绘制概率图相关系数图

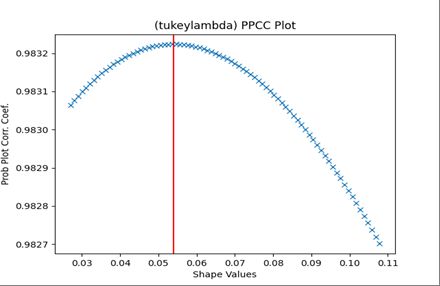
Res = stats.probplot(raw_in, sparams=(lambda,), dist=‘tukeylambda’, fit=True, plot=None, rvalue=False)，res[1][0]即${\sigma }_{TL}$

1.2.5 建模联合参数分布

不同的ISO对应着不同的噪声参数，因此需要建立ISO与噪声参数之间的联系，以便在连续的ISO范围内以耦合的方式采样对应的噪声参数。由于系统的总体增益K与ISO基本是线性的比例关系，因此对K和其他噪声参数之间的数学关系进行建模即可。
建模流程为：
① 每个ISO下标定系统总体增益K，得到一个K序列；
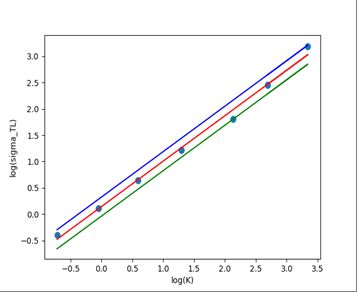
② 分别对$log(K)$和$log({\sigma }_r)$、$log({\sigma }_{TL})$进行线性最小二乘回归得到$a_r$, $b_r$, $a_{TL}$, $b_{TL}$，根据得到的线性方程计算模拟值和真实值的方差${\hat{\sigma }}_r$和${\hat{\sigma }}_{TL}$；再根据下图公式进行参数采样。

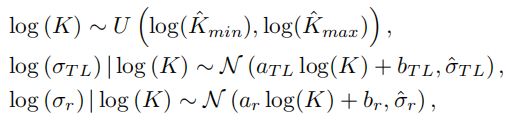
1.3 收集了一个极低光去噪数据集ELD

为了系统地研究所提出噪声模型的通用性，收集了一个极弱光数据集，包括10个室内场景和来自多个品牌的4个相机设备（SonyA7S2, NikonD850, CanonEOS70D,CanonEOS700D），用于基准测试。
摄像机安装在一个坚固的光学台上，由远程软件控制，以避免摄像机运动造成的失调，场景由自然或直流光源照明，以避免交流光的闪烁效果。数据采集步骤如下：

对于每个场景每个相机设备每个ISO gh：首先在基础ISO（gb=100）和曝光时间t设置下拍摄一个曝光良好的参考图像，然后在使用不同低光因子f降低曝光时间的设置下采集噪声图像，以模拟极端低光条件。然后拍摄另一张类似于第一张的参考图像，以确保没有发生意外错误（例如，剧烈的照明变化或意外的摄像机/场景运动）。
作者选择了三个ISO级别（800、1600和3200）和两个低光因子（100、200），总共得到240对（3×2×10×4）原始图像对。数据集的“伪”ISO高达640000（32000×200）。

2. 参考

Physics-based Noise Modeling for Extreme Low-light Photography