常见排序--归并排序(递归和非递归)+计数排序
文章目录
- 4 归并排序
-
- 4.1 递归形式
- 4.2非递归形式
- 5计数排序
- 6总结
4 归并排序
基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:(其实就是一个后序排序,先分解到一个有序再合并)
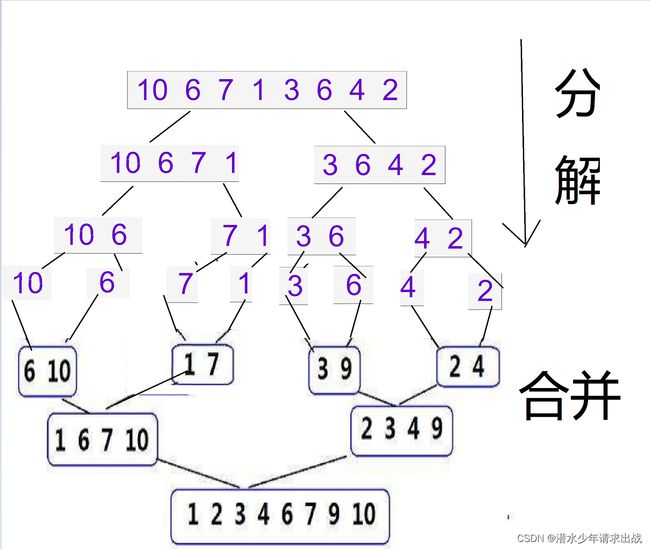
4.1 递归形式
难点在于合并:举个简单例子:就是两个数组合并成一个有序的数组方法类似
方法:就是两个数组一个一个数比大小,小的拿下来(我们需要一个额外的数组-叫tmp来实现),存在tmp数组中拿下来的数组往后移动到下一个数,然后我们可以至少保证有一个数组被拿完,剩下的我们依次拿下来,最后再把tmp赋给原来的数组中。
(begin1: 和begin2:是两个数组的开头。 )
这一块这样实现:
int begin1 = left, begin2 = mid + 1;
int end1 = mid, end2 = right;
int i = begin1; //begin1不一定是0
while (begin1<=end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
//三种可能。1.左半部分走完了,右半部分未走完。2.右半部分走完了,左半部分未走完。
//3.都走完了。我们其实不用关心,谁还剩下。
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
注意:最后tmp需要释放。
代码块:
void _mergeSort(int* a, int begin, int end, int* tmp)
{
assert(a);
if (begin >= end)
return;
int left = begin;
int right = end;
int mid = left + (right - left) / 2;//(right+left)/2
_mergeSort(a, left, mid, tmp);
_mergeSort(a, mid + 1, right, tmp);
int begin1 = left, begin2 = mid + 1;
int end1 = mid, end2 = right;
int i = begin1; //begin1不一定是0
while (begin1<=end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
//三种可能。1.左半部分走完了,右半部分未走完。2.右半部分走完了,左半部分未走完。
//3.都走完了。我们其实不用关心,谁还剩下。
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
void MergeSort(int* a, int n)
{
assert(a);
int* tmp = (int*)calloc(n, sizeof(int));
if (tmp == NULL)
{
printf("calloc fail");
exit(-1);
}
_mergeSort(a, 0, n - 1, tmp);
free(tmp);
}
4.2非递归形式
非递归说白了我们直接从合并那一步开始,我们手搓一个递归形成。
非递归排序与递归排序相反,将一个元素与相邻元素构成有序数组,再与旁边数组构成有序数组,直至整个数组有序。
要有mid指针传入,因为不足一组数据时,重新计算mid划分会有问题需要指定mid的位置
图有助于理解:

到这一步了,这不就简单 我们先看下面一段代码
void MergeSortNonR(int* a, int n)
{
assert(a);
int* tmp = (int*)calloc(n, sizeof(int));
if (tmp == NULL)
{
printf("calloc fail");
exit(-1);
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, begin2 = i + gap;
int end1 = i + gap - 1, end2 = i + 2 * gap - 1;
int j = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
//三种可能。1.左半部分走完了,右半部分未走完。2.右半部分走完了,左半部分未走完。
//3.都走完了。我们其实不用关心,谁还剩下。
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
}
memcpy(a, tmp, n * sizeof(int));
gap *= 2;
}
free(tmp);
}
有问题吗?
先看一张每组的begin和end的范围图:

我们清晰的发现了,它越界了。
int begin1 = i, begin2 = i + gap;
int end1 = i + gap - 1, end2 = i + 2 * gap - 1;
我们可以知道begin1不会越界,其它都有可能。这个时候我们需要修边。(注意不要把越界的都改为n-1,这样可能会导致我们最后从tmp复制回去就丢失数据了)
操作:我们可以让它范围不成立或只有一个值
//修边
if (end1 >= n)
{
end2 = end1 = n - 1;
begin2 = n;
}
else if (begin2 >= n)
{
end2 = n - 1;
begin2 = n;
}
else if (end2 >= n)
{
end2 = n - 1;
}
综上可得
代码块:
void MergeSortNonR(int* a, int n)
{
assert(a);
int* tmp = (int*)calloc(n, sizeof(int));
if (tmp == NULL)
{
printf("calloc fail");
exit(-1);
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, begin2 = i + gap;
int end1 = i + gap - 1, end2 = i + 2 * gap - 1;
//修边
if (end1 >= n)
{
end2 = end1 = n - 1;
begin2 = n;
}
else if (begin2 >= n)
{
end2 = n - 1;
begin2 = n;
}
else if (end2 >= n)
{
end2 = n - 1;
}
int j = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
//三种可能。1.左半部分走完了,右半部分未走完。2.右半部分走完了,左半部分未走完。
//3.都走完了。我们其实不用关心,谁还剩下。
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
}
memcpy(a, tmp, n * sizeof(int));
gap *= 2;
}
free(tmp);
}
5计数排序
这个借助哈希桶部分性质,其实没什么。
这个实用于小范围集中重复的整数部分。我们需要借助一个数组来完成–tmp。
(简单理解就是我们把每个数的值就是一个下标,我们把这个数出现几次就在tmp数组下标所存的数就是几。负数就不适合)
思路:实际上,我们可以把最小的整数存再第一个。怎么做哪?对我们可以每个数减去最小值–这样既保证了负数可以存也杜绝空间浪费。最后我们再依次取出就可以了
void CountSort(int* a, int n)
{
assert(a);
int min = a[0], max = a[0];
for (int i = 1; i < n; ++i)
{
if (min > a[i])
min = a[i];
if (max < a[i])
max = a[i];
}
int range = max - min + 1;
int* tmp = (int*)calloc(range, sizeof(int));
if (tmp == NULL)
{
printf("calloc fail");
exit(-1);
}
for (int i = 0; i < n; ++i)
{
tmp[a[i] - min]++;
}
int i = 0;
for (int j = 0; j < range; ++j)
{
while (tmp[j]--)
{
a[i++] = j + min;
}
}
free(tmp);
}