FP64、FP32、FP16、FP8简介

目录

1、单精度浮点数FP32的表示

2、半精度浮点数FP16的表示

3、双精度浮点数FP64的表示

4、FP8

5、写在最后

---

1、单精度浮点数FP32的表示

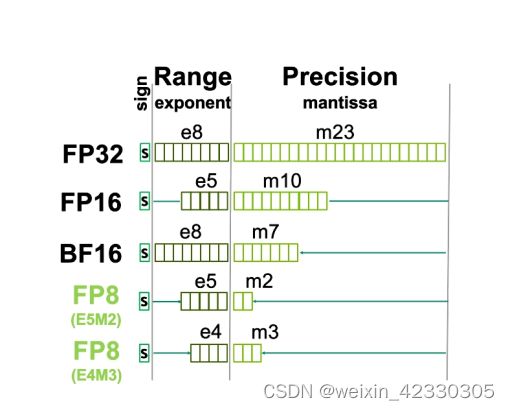
浮点数由三部分组成：符号位、指数部分、尾数部分

以单精度浮点数为例，如图所示，符号位为1bit、指数位8bit、尾数位23bit

表达方式如下：

−1 × 2 − ×1.

其中bias决定了数的取值范围，默认值为127 

exponent-bias表示对1.小数点右移的位数 

为什么是1.而不是0.、或者0. 0 呢？

举个例子，十进制整数17可以表示为：1 × 25 × (0.10001)2，也可以表示为：1 × 26 × (0.010001)2

这样就给计算机处理增加了复杂性，为了同一表示，规定尾数部分最高位必须是1，也就是说尾数必须以0.1开头，对指数做相应的调整，这称为正规化（Normalize）。由于尾数部分的最高位必须是1，这个1就不必保存了，可以节省出一位来用于提高精度，我们说最高位的1是隐含的（Implied）。

因此，十进制整数17表示为

即：

1 × 24 × (1.0001)2

一些特殊情况：

1）exponent=0，且mantissa=0；表示数字0

2）exponent=0，且mantissa != 0；表示一个非常小的数

3）exponent=全f，且mantissa=0；表示无穷大。如果符号位为0，表示正无穷；如果符号位为1，表示负无穷

4）exponent=0，且mantissa != 0；非法。

举例：对于十进制数3.25，单精度浮点数如何表示？

0 10000000 10100000000000000000000

如图：

Sign=0

Exponent = 10000000(二进制)/128(十进制)

Bias = 127

Exponent - Bias = 1（小数点右移1位） 

1.=1.101

小数点移位后：(11.01)2

1 × 21 + 1 × 20+0 × 2−1+ 1 × 2−2 =  2 + 1 + 0 + 0.25 = 3.25

2、半精度浮点数FP16的表示

单精度浮点数除了exponent和mantissa的长度、bias的值外，其余和单精度浮点数都一样

如图所示：

符号位为1bit、指数位5bit、尾数位10bit

Bias = 15

3、双精度浮点数FP64的表示

符号位为1bit、指数位11bit、尾数位52bit

Bias = 1023

4、FP8

FP8首次出现在2022年4月，Nvidia 发布的最新一代高性能GPU架构：H100。H100 TensorCore中引入了一种新的浮点类型FP8

如图所示：

有两种形式，E5M2和E4M3，对于E5M2，指数位5bit、尾数位2bit

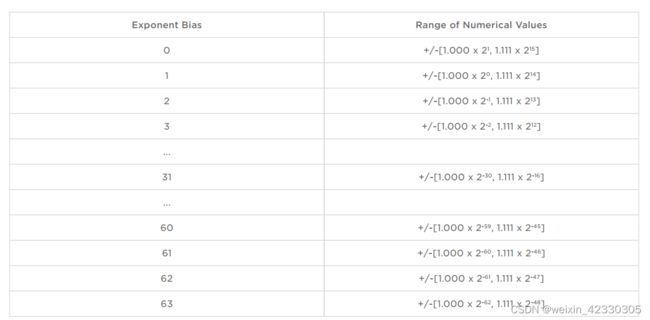
bias的值和对应的FP8所能表示的数的取值范围如下表：

对于E4M3，指数位4bit、尾数位3bit

bias的值和对应的FP8所能表示的数的取值范围如下表：

5、写在最后

1）小程序

根据IEEE-754标准，十进制、十六进制、二进制、FP32转化

IEEE-754 Floating Point Converter (h-schmidt.net)

2）思考：FP64、FP32、FP16、FP8之间如何转换？