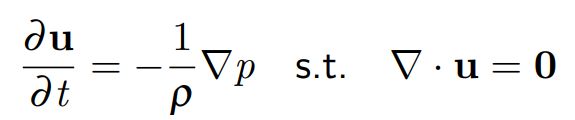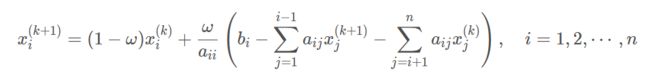NiagaraFluids代码分析1:力学部分
力学部分
UE5正式版中,Niagara Fluid插件提供了相对完整的流体仿真解决方案,其中模拟部分采用了混合欧拉-拉格朗日视角,使用了PIC/FLIP方法。
本文将就3DLiquidDamBreak粒子系统为出发点,分析其中粒子位置更新的计算过程。
不完整或有错误的地方将在后续学习过程中逐步完善。
1 初始化数据
1.1 Grid 3D Set Resolution
这一部分初始化了Grid的分辨率,即欧拉网格的分辨率。代码如下:
float CellSize = max(WorldGridExtents.z, max(WorldGridExtents.x, WorldGridExtents.y)) / NumCellsMaxAxis;
NumCellsX = floor(WorldGridExtents.x / CellSize);
// step1:取各个方向尺寸的最大值,统一cellsize,再计算每个方向有多少个cell
...
// step2:处理特殊情况,为部分NumCells+1
Out_WorldGridExtents = float3(NumCellsX, NumCellsY, NumCellsZ) * CellSize;
// step3:用上边得到的cellsize和cellnum重新计算在世界空间下模拟的尺寸
1.2 粒子初速度
v p 1 = v p 0 + ( ( f p + g ) Δ t ) v_{p1} = v_{p0}+((f_p + g) \Delta t) vp1=vp0+((fp+g)Δt)
下边对照之前所学的混合欧拉-拉格朗日视角过程,逐层分析
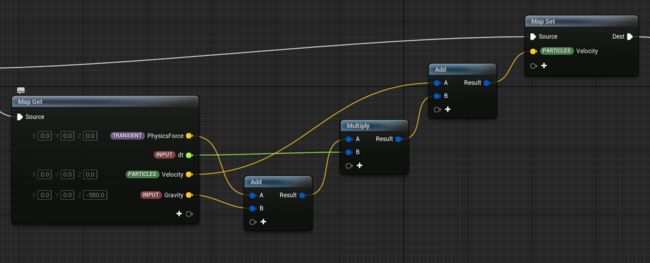
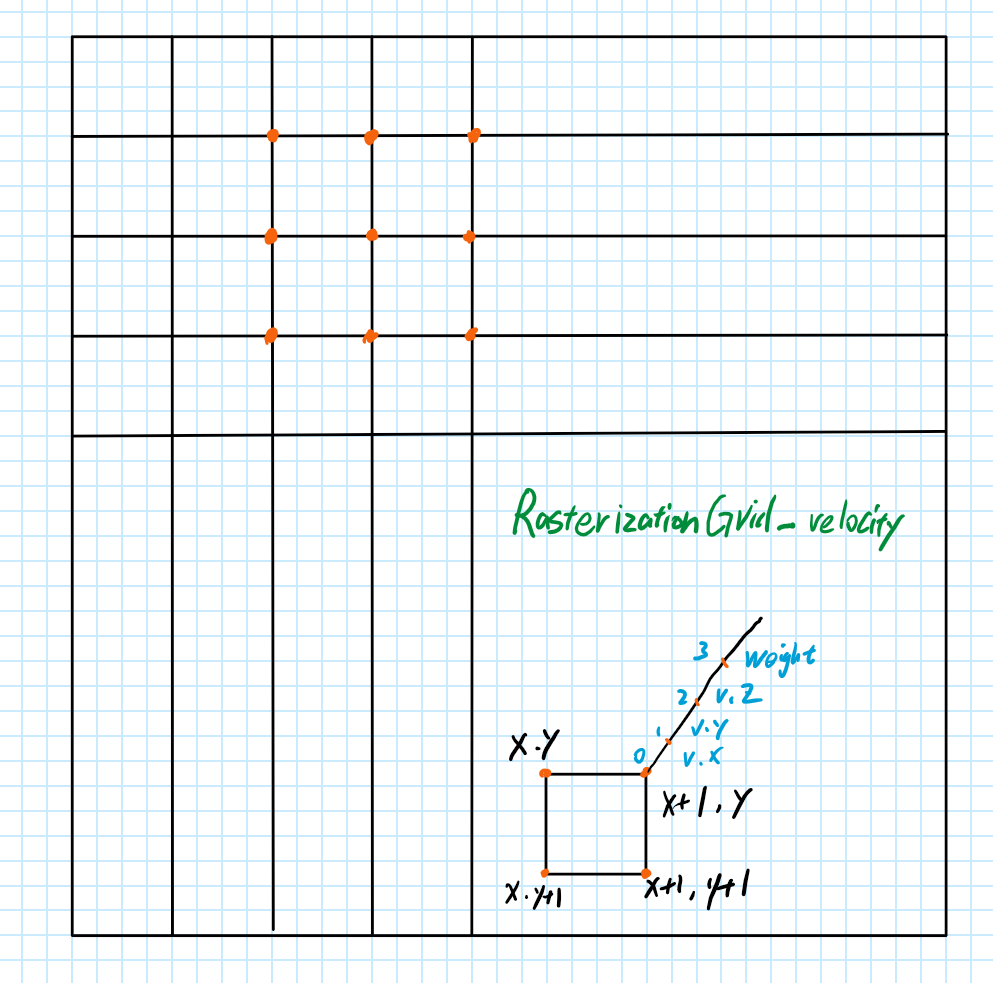
2 P2G Particle to Grid transfer
对应粒子系统中的Rasterize Particles:Grid 3D FLIP Rasterize Particles部分
int IGNORE = 0;
int XIndexInt = floor(Index.x);
int YIndexInt = floor(Index.y);
int ZIndexInt = floor(Index.z); //向下取整到对应的Index,相当于直接存到了粒子所在网格的左上角
for (int x = 0; x <= 1; ++x) {
for (int y = 0; y <= 1; ++y) {
for (int z = 0; z <= 1; ++z) {
const float GridWeightXYZ = 1;//代码中权重均取1
RasterizationGrid_velocity.InterlockedAddFloatGridValueSafe(XIndexInt+x, YIndexInt+y, ZIndexInt+z, 0, GridWeightXYZ*Velocity.x, IGNORE);
RasterizationGrid_velocity.InterlockedAddFloatGridValueSafe(XIndexInt+x, YIndexInt+y, ZIndexInt+z, 1, GridWeightXYZ*Velocity.y, IGNORE);
RasterizationGrid_velocity.InterlockedAddFloatGridValueSafe(XIndexInt+x, YIndexInt+y, ZIndexInt+z, 2, GridWeightXYZ*Velocity.z, IGNORE);
RasterizationGrid_velocity.InterlockedAddFloatGridValue(XIndexInt+x, YIndexInt+y, ZIndexInt+z, 3, GridWeightXYZ, IGNORE); //分别累加xyz方向的速度到格点上、权重
BoundaryGrid.SetGridValue(XIndexInt+x, YIndexInt+y, ZIndexInt+z, BoundaryIndex, 3, IGNORE); //记录BoundaryIndex到BoundaryGrid
}}}
参考:Niagara RasterizationGrid3D Data Interface
RasterizationGrid3D可用于迭代源为Particle时并行的累加(InterlockedAddFloatGridValueSafe)
3 Grid operations
3.1 Boundaries conditions
在TransientGrid上存储边界类型和固体速度
遍历网格TransientGrid,存储当前Index处的边界类型,用于后续计算:
//边界类型
const int FLUID_CELL = 0; // 0 流体内部
const int SOLID_CELL = 1; // 1 固体边界
const int EMPTY_CELL = 2;
和边界处的固体的速度SolidVelocity
3.2 PIC方法
修正:这里其实可以看作还是P2G的一部分,做的还是在gather速度和处理边界
从RasterizationGrid_velocity中gather速度,若cell处于边界上,则gather所有附近的类型为fluid的cell
代码部分只保留了关键部分
// 从RasterizationGrid_velocity中Gather速度
Grid.GetFloatGridValue(IndexX, IndexY, IndexZ, 0, OutVelocity.x);
Grid.GetFloatGridValue(IndexX, IndexY, IndexZ, 1, OutVelocity.y);
Grid.GetFloatGridValue(IndexX, IndexY, IndexZ, 2, OutVelocity.z);
Grid.GetFloatGridValue(IndexX, IndexY, IndexZ, 3, TmpWeight);
OutVelocity /= TmpWeight;
// if we have a boundary cell, then gather value from closest neighbor cell
// 如果在边界上
[branch]
if (CellType != FLUID_CELL)
{
// 共采样了3x3x3 = 27个 跳过了不是FLUID_CELL类型的cell
for (int xx = -ExtrapolationHalfWidth; xx <= ExtrapolationHalfWidth; ++xx) {
for (int yy = -ExtrapolationHalfWidth; yy <= ExtrapolationHalfWidth; ++yy) {
for (int zz = -ExtrapolationHalfWidth; zz <= ExtrapolationHalfWidth; ++zz) {
// only extrapolate from fluid cells
// don't extrapolate from the boundary of the domain to allow particles to pass through as ballistic when they leave
if (TmpCellType == FLUID_CELL)
{
float Weight = 1./length2(float3(xx,yy,zz));
// gather邻居
Grid.GetFloatGridValue(IndexX+xx, IndexY+yy, IndexZ+zz, 0, TmpVelocity.x);
Grid.GetFloatGridValue(IndexX+xx, IndexY+yy, IndexZ+zz, 1, TmpVelocity.y);
Grid.GetFloatGridValue(IndexX+xx, IndexY+yy, IndexZ+zz, 2, TmpVelocity.z);
Grid.GetFloatGridValue(IndexX+xx, IndexY+yy, IndexZ+zz, 3, TmpWeight);
TmpVelocity /= TmpWeight; // 所在cell的速度
OutVelocity += TmpVelocity * Weight; // 按照距离平方的倒数作为权重累加
TotalWeight += Weight; // 累加权重
}
}}}
OutVelocity /= TotalWeight;
}
gather得到的速度,直接作为SimGrid的 v i t v^{t}_i vit和 v i t + 1 v^{t+1}_i vit+1(aka. StartVelocity and Velocity)
3.3 Projection
3.3.1 Compute Divergence 计算散度
Div = (Vx_right - Vx_left + Vy_up - Vy_down + Vz_front - Vz_back) / (2. * dx);
对应 ∇ ⋅ u \nabla·u ∇⋅u
计算完成后将Div赋值给TemporaryGrid,同时初始化PressureGrid中Pressure值为0
3.3.2 Solve Pressure 解算压力
使用SOR方法迭代50次解算出一个压力场(即Pressure Grid中的值),使散度为0
代码中使用了Red-Black Successive Over-Relaxation (SOR)方法
其中
SOR方法参考:线性方程组的SOR迭代法
Red-Black Ordering方法参考:Red-Black Ordering Lecture 67 Numerical Methods for Engineering
首先,介绍本文中需要求解的矩阵 Ax = b,参考Games201学习笔记3:欧拉视角4. Prjection部分
压力对加速度的贡献
对方程展开, ∂ u ∂ t \frac{\partial u}{\partial t} ∂t∂u替换为下一时刻速度-当前速度,移项,左右同时求散度 ∇ ⋅ \nabla· ∇⋅由于下一时刻散度为0,所以 ∇ ⋅ u ∗ = 0 \nabla·u^* = 0 ∇⋅u∗=0项消去,化简的到最后结果
左边一项采用中心差分法近似拉普拉斯(三维空间下为上下左右前后的邻居,其中4 p i , j p_{i,j} pi,j中的4替换为周围cell类型为fluid或empty的个数(FluidCellCount),代码如下
float Scale = dx / dt;
int CellType_right = round(B_right);
if (CellType_right == SOLID_CELL)
{
FluidCellCount--;//从6递减
BoundaryAdd += Scale * (Velocity.x - SV_x_right);//固体边界的相对速度提供的压力
P_right = 0;//若边界不是fluid则压力为0
}
else if (CellType_right == EMPTY_CELL)
{
P_right = 0;
}
右边式子中的散度已知,ρ取了1,故得到以下等式
1 Δ x 2 ( − F l u i d C e l l C o u n t × P c e n t e r + P r i g h t + P l e f t + P u p + P d o w n + P f r o n t + P b a c k + P B o u n d a r y ) = ∇ ⋅ u Δ t \frac{1}{\Delta x^2 }(-FluidCellCount \times P_{center} +P_{right} + P_{left} + P_{up} + P_{down} + P_{front} + P_{back} + P_{Boundary}) = \frac{\nabla·u}{\Delta t} Δx21(−FluidCellCount×Pcenter+Pright+Pleft+Pup+Pdown+Pfront+Pback+PBoundary)=Δt∇⋅u
化简
P c e n t e r = ( P c e n t e r + P r i g h t + P l e f t + P u p + P d o w n + P f r o n t + P b a c k + P B o u n d a r y − Δ x 2 × ∇ ⋅ u Δ t ) / F l u i d C e l l C o u n t P_{center} = (P_{center} +P_{right} + P_{left} + P_{up} + P_{down} + P_{front} + P_{back} +P_{Boundary} - \frac{\Delta x^2 \times \nabla·u}{\Delta t})/FluidCellCount Pcenter=(Pcenter+Pright+Pleft+Pup+Pdown+Pfront+Pback+PBoundary−ΔtΔx2×∇⋅u)/FluidCellCount
对应线性方程Ax=b,其中右边的量均能在一次迭代中求出,作为b,单位向量I作为A, P c e n t e r P_{center} Pcenter作为x
解方程使用了Red-Black Successive Over-Relaxation (SOR)方法
先来谈Red-Black:
每次迭代,只计算Grid中标记为黑色的部分,下一次迭代,计算红色的部分,交替进行。判断当前格点颜色的代码如下,CellParity的值为0或1表示红黑
int SliceParity = (IndexZ + IterationIndex) % 2;
int RowParity = (IndexY + SliceParity+1) % 2;
int CellParity = (IndexX + RowParity ) % 2;
// will do red-black SOR
// add 1 since we want to expose a 0-1 parameter
Weight = CellParity * min(1.93, Relaxation + 1);
再来谈SOR:Successive Over Relaxation(逐次超松弛),是Gauss-Seidel迭代法的加速,引入了ω加速迭代。具体推导参考上边链接,这里直接把结果拿来了
前边提到A为单位矩阵,故只有aii=1,其他为0,化简如下,ω对应上述的weight,经过红黑优化后的权重,具体使用时Relaxation = 0.95,故ω=1.93或0
x i k + 1 = ( 1 − ω ) x i k + ω b i x^{k+1}_i = (1-\omega) x^k_i + \omega b_i xik+1=(1−ω)xik+ωbi
P c e n t e r = ( P c e n t e r + P r i g h t + P l e f t + P u p + P d o w n + P f r o n t + P b a c k + P B o u n d a r y − Δ x 2 × ∇ ⋅ u Δ t ) / F l u i d C e l l C o u n t P_{center} = (P_{center} +P_{right} + P_{left} + P_{up} + P_{down} + P_{front} + P_{back} +P_{Boundary} - \frac{\Delta x^2 \times \nabla·u}{\Delta t})/FluidCellCount Pcenter=(Pcenter+Pright+Pleft+Pup+Pdown+Pfront+Pback+PBoundary−ΔtΔx2×∇⋅u)/FluidCellCount
综上,对应代码
if (FluidCellCount > 0)
{
float JacobiPressure = (P_right + P_left + P_up + P_down + P_front + P_back - dx * dx * Divergence / dt + BoundaryAdd) / FluidCellCount;
Pressure = (1.f - Weight) * P_center + Weight * JacobiPressure;
}
共迭代50次后,得到一个散度近似为0的压力场,记录在Pressure Grid中
3.3.4 Project Pressure
将p带入公式求速度,同时处理边界问题
step1:求梯度 ∇ p \nabla p ∇p,由邻居的pressure近似梯度Gradient
Grad = float3(S_right - S_left, S_up - S_down, S_front - S_back) / (2.0 * dx);
step2:求加速度
step3:处理边界(以左右边界为例,后边处理上下,前后同理)
//只考虑一边是边界,而非左右都是边界的极端情况
if (CellType_left == SOLID_CELL)
{
VelocityOut.x = SV_x_left; //左边为边界,则从边界中读取速度并赋值
}
else if (CellType_right == SOLID_CELL)
{
VelocityOut.x = SV_x_right;
}
else
{
VelocityOut.x = Velocity.x; //上下都不是边界,则正常赋值
}
得到的速度赋给SimGrid保存
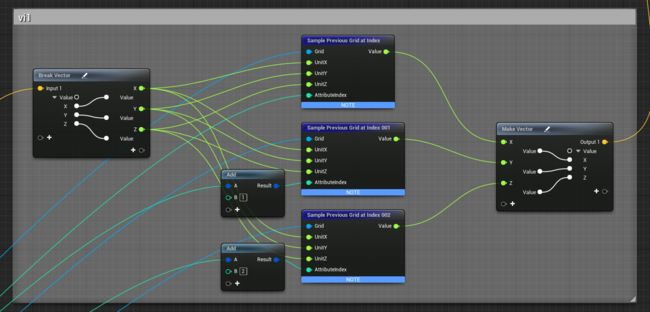
3.3.5 Extrapolate Velocities Again
在SimGrid上处理cell类型为边界的值,相当于模糊了边界速度值,同3.2
3.4 小结
至此,新的速度场已经计算得到,存储在SimGrid中,下边将使用PIC/FLIP方法,更新速度到粒子上。旧的速度场在第一次Extrapolate Velocities时,也记录到了SimGrid,使用了不同的下标(AttributeIndex)
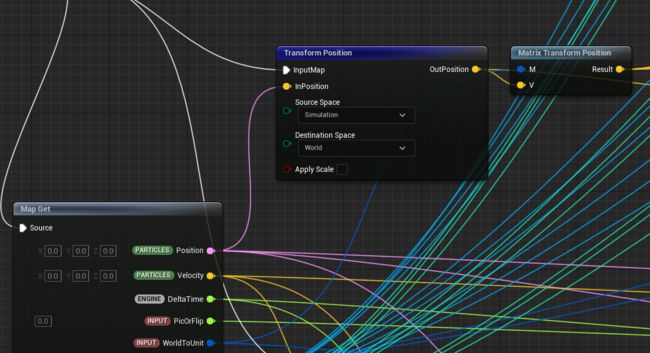
4 G2P Grid to Particle transfer
这里开始Simulation Stage的迭代源为particle,之前的迭代源为Grid
UE这里使用的方法为将particle的坐标进行2次矩阵乘法(SimulationToWorld,WorldToUnit),输出位置为UnitPos,一般是0-1的float,超出范围的不再更新速度,只按照当前速度更新位置
然后用unitpos在SimGrid网格中插值采样得到速度,插值的代码没有看到,盲猜是三维空间下的线性插值。
5 Particle operations
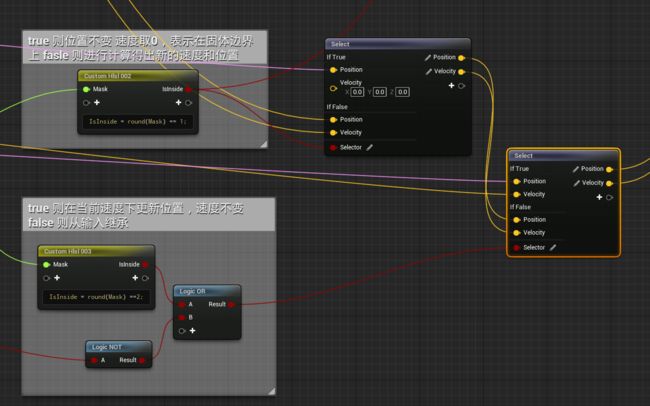
5.1 Move particle
边界的处理:
若粒子处于固体边界中,速度取0,位置不变
若粒子处于空cell中,速度不变,位置按照当前粒子速度乘以dt更新
若不在以上边界,速度的更新则按照PIC/FLIP方法混合更新。
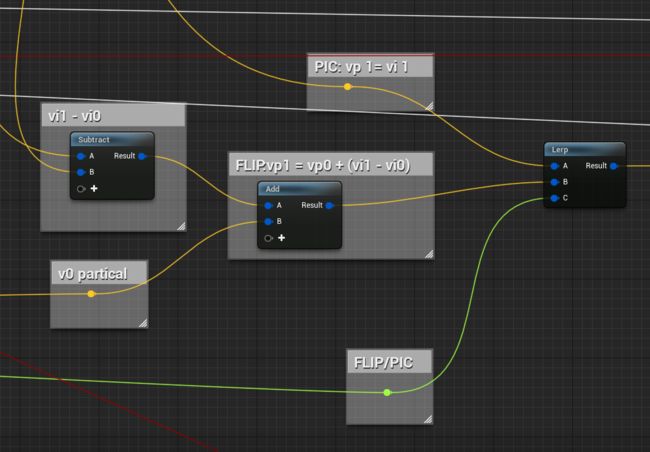
回顾这2种方法:
- PIC: v p t + 1 v^{t+1}_p vpt+1 = v i t + 1 v^{t+1}_i vit+1 直接从网格中采样得到并更新
- FLIP: v p t + 1 v^{t+1}_p vpt+1 = v p t v^{t}_p vpt + gather( v i t + 1 v^{t+1}_i vit+1- v i t v^{t}_i vit) 从网格中采样速度的增量,累加到原来的速度上
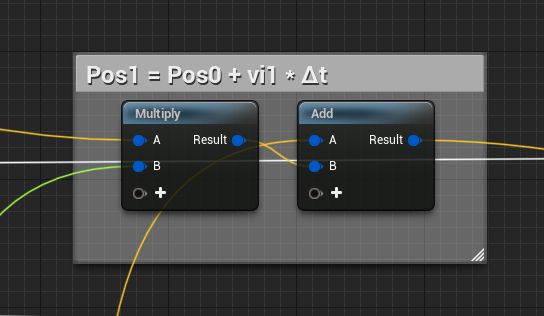
蓝图中如下表示
位置的更新略有不同,完全使用了PIC方法,即直接使用网格中采样得到新的速度场更新粒子位置
6 总结
至此,力学部分的计算过程总结完成,遗留了渲染得到水的部分,将在下一篇中更新