LeetCode——遍历序列构造二叉树
105从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均无重复元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列
原题目链接:https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
思路:
这里给的两个数组,第一个数组是前序遍历的内容,第二个是中序遍历的内容,前序遍历是根,左,右,由此可以确定根节点,但是不能确定左子树和右子树是怎么分布的,但是中序遍历可以根据确定的第一个根来判断左子树和右子树的区间:

前序遍历的数组走向第一个元素就代表找到了第一个根结点,在第二个数组中找到相对应元素的位置就好了(注意这里是元素没有重复的,不然这种方法是行不通的),这时3的左边就是左子树,3的右边就是右子树。
上面的步骤能确定一个结点是3,然后递归分别进入第二个数组中左子树和右子树的区间中,进入递归之后第一个数组的指针指向第二个元素。
因为第一个数组是前序遍历,所以进入左子树的递归之后就能先查到左子树的第一个根,也就是9,然后去查看他的左子树和右子树发现都是空,所以就直接返回,也确定了3的的左子树的结构,然后返回到3,再进入3的右子树:

代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* section(vector<int>& preorder, vector<int>& inorder,int& pos,int begin,int end)
{
if(begin > end)//只要区间不合法,就返回空
return nullptr;
TreeNode* root = new TreeNode(preorder[pos]);//先构建根
int i = begin;//这里是查找区间的下标,不能从零开始
while(i <= end)
{
if(preorder[pos] == inorder[i])//找到和第一个数组相同的元素,用于区分左子树和右子树
break;
i++;
}
pos++;//让pos继续往后走,遍历第一个数组
root->left = section(preorder,inorder,pos,begin,i-1);//左区间
root->right = section(preorder,inorder,pos,i+1,end);//右区间
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int pos = 0;//用来储存第一个数组遍历的值
int begin = 0;//第二个数组的区间,头
int end = inorder.size() - 1;//第二个数组的区间,尾
return section(preorder,inorder,pos,begin,end);
}
};
106从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗二叉树。
示例 1:
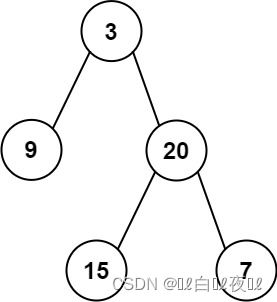
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
提示:
1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由不同的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历
原题目链接:https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/
这道题与上一道题是类似的:
第一个数组是中序遍历(左,根,右),第二个数组是后序遍历(左,右,根),第一个数组依然用于分区间,第二个数组可以反向确定根,然后先走右子树再走左子树。
class Solution {
public:
TreeNode* section(vector<int>& inorder, vector<int>& postorder,int& pos,int begin,int end)
{
if(begin > end)
return nullptr;
TreeNode* root = new TreeNode(postorder[pos]);//先构建根
int i = begin;
while(i <= end)
{
if(inorder[i] == postorder[pos])
break;
i++;
}
pos--;//从后往前遍历
root->right = section(inorder,postorder,pos,i+1,end);//先进入右子树
root->left = section(inorder,postorder,pos,begin,i-1);//在进入左子树
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int pos = inorder.size() - 1;//用来储存第二个数组遍历的值
int begin = 0;//第一个数组的区间,头
int end = inorder.size() - 1;//第二个数组区间,尾
return section(inorder,postorder,pos,begin,end);
}
};

