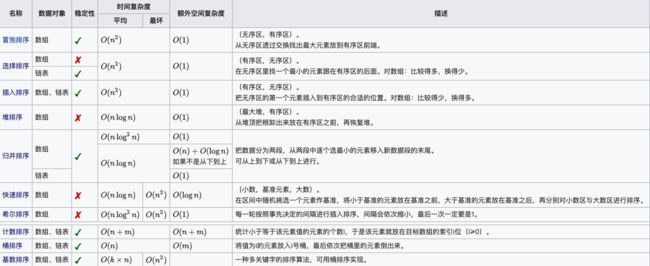
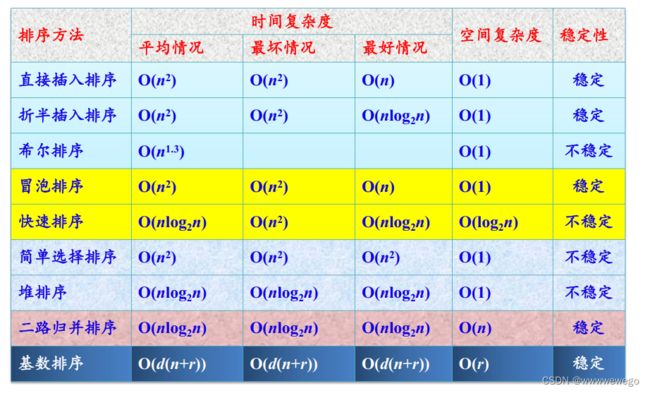
内部排序算法

总结

1.0 十大经典排序算法 | 菜鸟教程本系列算法整理自：https://github.com/hustcc/JS-Sorting-Algorithm 同时也参考了维基百科做了一些补充。 排序算法是《数据结构与算法》中最基本的算法之一。 排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序..https://www.runoob.com/w3cnote/ten-sorting-algorithm.html

 

排序算法的稳定性_丶栉尊的博客-CSDN博客_排序算法稳定性排序算法稳定性：意思就是说大小相同的两个值在排序之前和排序之后的先后顺序不变，这就是稳定的。（1）冒泡排序：原理是通过相邻的两个元素作比较，把小的向前移或者把大的向后移，移动就是交换这两个元素。如果说碰到相等的两个元素是不会做处理的。所以是稳定的排序。（2）选择排序：原理是从第一个元素开始，在之后的所有元素中选择一个最小的交换过来。如果说原序列中第一个元素和第二个元素相等，第三个元素...https://blog.csdn.net/xjm1018/article/details/88547231

插入类排序

简单插入排序

#include

//简单插入排序
void InsSort(int r[], int n)
{
	int j;
	for (int i = 2; i <= n; i++)
	{
		r[0] = r[i];//利用监视哨r[0]
		j = i - 1;
		while (r[0] < r[j])//从小到大排序
		{
			r[j + 1] = r[j];//寻找插入位置，并挪出该位置
			j--;
		}
		r[j + 1] = r[0];//插入
	}
}

void main()
{
	int r[10] = { 0,6,4,3,88,89,56,34,3,1 };
	int n = 10;
	InsSort(r, n-1);//r[0]不参与排序
	for (int k = 0; k < n; k++)
		printf("%d\t", r[k]);
	return;
}

折半插入排序

#include

//折半插入排序
void BinSort(int r[], int n)
{
	int j, low, high, mid;
	for (int i = 2; i <= n; i++)
	{
		r[0] = r[i];//利用监视哨r[0]
		low = 1;
		high = i - 1;
		while (low <= high)
		{
			mid = (low + high) / 2;
			if (r[0] >= r[mid])//等号保证稳定性
				low = mid + 1;
			else
				high = mid - 1;
		}
		for (j = i - 1; j >= low; j--)
			r[j + 1] = r[j];//挪出位置
		r[low] = r[0];
	}
}

void main()
{
	int r[10] = { 0,6,4,3,88,89,56,34,3,1 };
	int n = 10;
	BinSort(r, n-1);//r[0]不参与排序
	for (int k = 0; k < n; k++)
		printf("%d\t", r[k]);
	return;
}

希尔排序

#include
//希尔排序
void ShellInsert(int r[], int n,int delta)//一个子序列的直接插入排序
{
	int j;
	for (int i = 1+delta; i <= n; i++)
	{
		r[0] = r[i];//利用监视哨r[0]
		j = i - delta;
		while (r[0] < r[j]&&j>0)//从小到大排序
		{
			r[j + delta] = r[j];//寻找插入位置，并挪出该位置
			j=j-delta;
		}
		r[j + delta] = r[0];//插入
	}
}

void ShellSort(int r[], int n, int d[], int m)//多次直接插入排序
{
	for (int i = 0;i < m;i++)
		ShellInsert(r, n,d[i]);
}

void main()
{
	int r[20] = { 0,6,4,3,88,89,56,34,3,1,122,232,334213,3,32,232,23,789,343,45};
	int n = 20;
	int d[3] = { 7,3,1 };
	int m = 3;
	ShellSort(r, n-1,d,m);//r[0]不参与排序
	for (int k = 0; k < n; k++)
		printf("%d\t", r[k]);
	return;
}

交换类排序

冒泡排序

#include
//冒泡排序
void BubbleSort(int r[], int n)
{
	int x;
	for (int i = 0; i < n-1; i++)//从小到大排
	{
		for (int j = 0; j < n - 1 - i; j++)
		{
			if (r[j] > r[j + 1])//相等不交换，保证稳定性
			{
				x = r[j];
				r[j] = r[j + 1];
				r[j + 1] = x;//交换
			}
		}
	}
}

void main()
{
	int r[20] = { 0,6,4,3,88,89,56,34,3,1,122,232,334213,3,32,232,23,789,343,45};
	int n = 20;
	BubbleSort(r, n);
	for (int k = 0; k < n; k++)
		printf("%d\t", r[k]);
	return;
}

快速排序

当要排列的数据基本有序时，不利于发挥其长处。

在所写的几个算法中，平均比较次数最少。

#include
//快速排序
int QKPass(int r[], int low, int high)
{
	int x = r[low];
	while (low < high)
	{
		while (x <= r[high]&&lowr[high]
		{
			r[low] = r[high];
			low++;
		}
		while (x > r[low] && low < high)//不满足稳定性
			low++;
		if (low < high)
		{
			r[high] = r[low];
			high--;
		}
	}
	r[low] = x;//此时low=high
	return low;
}

void QKSort(int r[], int low, int high)//递归
{
	int key = QKPass(r, low, high);//key为基准，左边小于key，右边大于等于key
	if(key-1>=low)
		QKSort(r, low, key - 1);
	if (key + 1 <=high)
		QKSort(r, key + 1, high);
}

void main()
{
	int r[20] = { 0,6,4,3,88,89,56,34,3,1,122,232,334213,3,32,232,23,789,343,45};
	int n = 20;
	QKSort(r, 0,19);
	for (int k = 0; k < n; k++)
		printf("%d\t", r[k]);
	return;
}

选择类排序

简单选择排序

关键字的比较次数和初始排列顺序无关。

基本有序时，算法效率最差。

#include
//简单选择排序
void SelectSort(int r[], int n)//从小到大排
{
	for (int i = 0; i < n; i++)
	{
		int k = i;
		for (int j = i + 1; j < n; j++)
			if (r[j] < r[k])
				k = j;
		if (k != i)
		{
			r[i] += r[k];//不使用额外的空间，交换r[i]和r[k]
			r[k] = r[i] - r[k];
			r[i] -= r[k];
		}
	}
}

void main()
{
	int r[20] = { 0,6,4,3,88,89,56,34,3,1,122,232,334213,3,32,232,23,789,343,45};
	int n = 20;
	SelectSort(r,n);
	for (int k = 0; k < n; k++)
		printf("%d\t", r[k]);
	return;
}

堆排序

建初始堆，从n/2（向下取整）（最后一个非叶结点）开始筛选。从下往上把所有字树调整为堆。

#include
//堆排序
void sift(int r[], int k, int m)//重建堆，又称筛选法
//r[k....m]是以r[k]为根节点的完全二叉树
{
	int t = r[k];//暂存r[k]
	int i = k, j = 2 * k;//左子树
	bool finish = false;
	while (j <= m && !finish)
	{
		if (j + 1 <= m && r[j + 1] > r[j])//右子树存在，且右子树根的关键字更大，则沿右子树筛选
			j++;
		if (t >= r[j])
			finish = true;
		else
		{
			r[i] = r[j];
			i = j;
			j = 2 * i;//向下一层
		}
	}
	r[i] = t;
}

void CrtHeap(int r[], int n)//建初始化堆
//任一序列可以看成对应的完全二叉树，由底向上逐层把所有子树调整为堆
{
	for (int i = n / 2; i >= 1;i--)//r[0]不排序
		//最后一个非叶结点位于n/2（向下取整）
		sift(r, i, n);
}

void HeapSort(int r[], int n)
{
	CrtHeap(r, n);//初始化
	for (int i = n; i > 1; i--)
	{
		r[1] += r[i];//堆顶和堆尾互换
		r[i] = r[1] - r[i];
		r[1] = r[1] - r[i];
		sift(r, 1, i - 1);//调整为堆
	}
}

void main()
{
	int r[20] = { 0,6,4,3,88,89,56,34,3,1,122,232,334213,3,32,232,23,789,343,45 };
	int n = 20;
	HeapSort(r, n-1);//r[0]不参与排序
	for (int k = 0; k < n; k++)
		printf("%d\t", r[k]);
	return;
}

归并排序

先分解，后合并

辅助空间为O（n）

程序要再测试

#include
#include
//归并排序
void Merge(int r[], int low, int mid, int high)//合并两个有序序列
{
	int* A = (int*)malloc(sizeof(int) * (high - low + 1));
	int i = low, j = mid + 1, k = 0;
	while (i <= mid && j <= high)
	{
		//选择比较小的数
		if (r[i] <= r[j])
		{
			A[k] = r[i];
			k++; i++;
		}
		else
		{
			A[k] = r[j];
			k++; j++;
		}			
	}
	//将剩余的放到A中
	while (i <= mid)
		A[k++] = A[i++];
	while (j <= high)
		A[k++] = A[j++];
	for (i = low, k = 0; i <= high; i++, k++)
		r[i] = A[k];
	free(A);
}

void MergeSort(int r[], int low, int high)//递归
{
	int mid;
	if (low < high)
	{
		mid = (low + high) / 2;
		MergeSort(r, low, mid);
		MergeSort(r, mid + 1, high);
		Merge(r, low, mid, high);
	}
}
void main()
{
	int r[20] = { 0,6,4,3,88,89,56,34,3,1,122,232,334213,3,32,232,23,789,343,45 };
	int n = 20;
	MergeSort(r,0,19);
	for (int k = 0; k < n; k++)
		printf("%d\t", r[k]);
	return;
}

分配类排序

链式基数排序

基数排序是通过“ 分配” 和“ 收集” 过程来实现排序，不需要关键字的比较。
LSD MSD

代码还需测试

#include
#include
#include
//链式基数排序
#define MAXR 10//基数的最大值
#define MAXD 8//关键字位数的最大值
typedef struct node
{
	int data[MAXD];
	struct node* next;
}NODE;

void RadixSort(NODE* p, int r, int d)//r为基数，d为关键字位数
{
	NODE* head[MAXR], * tail[MAXR], * t;//t为p的尾指针
	int j,k;
	for (int i = d; i > 0; i--)
	{
		for (j = 0; j < r; j++)//初始化
			head[j] = tail[j] = NULL;

		while (p)//分配
		{
			k = p->data[i];//第k个链对
			if (!head[k])
			{
				head[k] = p;
				tail[k] = p;
			}
			else
			{
				tail[k]->next = p;//尾插法
				tail[k] = p;
			}
			p = p->next;
		}

		p = NULL;
		for (j = 0; j < r; j++)
		{
			if (head[j])
			{
				if (!p)
				{
					p = head[j];
					t = tail[j];
				}
				else
				{
					t->next = head[j];
					t = tail[j];
				}
			}
		}
		t->next = NULL;
	}
}

void main()
{
	NODE* p=(NODE * )malloc(sizeof(NODE)),*t;
	t = p;
	int r = 10, d = 3,m=5;//r为基数，d为关键字位数，m是关键字个数
	srand((unsigned)time(NULL));
	for (int i = 0; i < m; i++)
	{
		for (int j = 0; j < d; j++)
		{
			t->data[j] = rand() % 10;
			printf("%d\t", t->data[j]);
		}
		printf("\t");
		t = t->next;
	}
	t->next = NULL;
	return;
}