EfficientDet:可伸缩且高效的目标检测
目录
- 论文下载地址
- 代码下载地址
- 论文作者
- 模型讲解
-
- [背景介绍]
- [论文解读]
-
-
- [EfficientDet的效率]
- [双向特征金字塔网络]
-
-
- [结构方面]
- [融合方面]
-
- [EfficientDet]
-
-
- [EfficientDet结构]
- [复合标度]
-
-
- [代码解析]
- [实验结果]
-
-
- [不同目标检测网络之间的对比]
- [创新点的对比]
-
-
- [backbone与BiFPN]
- [不同结构特征网络的对比]
- [不同融合特征网络的对比]
- [复合标度的对比]
-
-
论文下载地址
[EfficientDet论文地址]
代码下载地址
[GitHub-unofficial]
论文作者
模型讲解
[背景介绍]
[Deep Learning for Generic Object Detection: A Survey] -[Paper] -[GitHub]
2013年R-CNN的提出,首次将深度学习的方法应用于目标检测领域,经过5年多的研究与发展,深度学习的方法已经成为目标检测普遍使用的方法,下图是自2013年以来提出的模型(截至2019年):
注意:本节所有图片截取自论文 ☛ https://arxiv.org/pdf/1809.02165v1.pdf

以下是目标检测常用的数据集及其信息,VOC、ILSVRC、COCO以及OID。

以下是评价目标检测器常用指标。
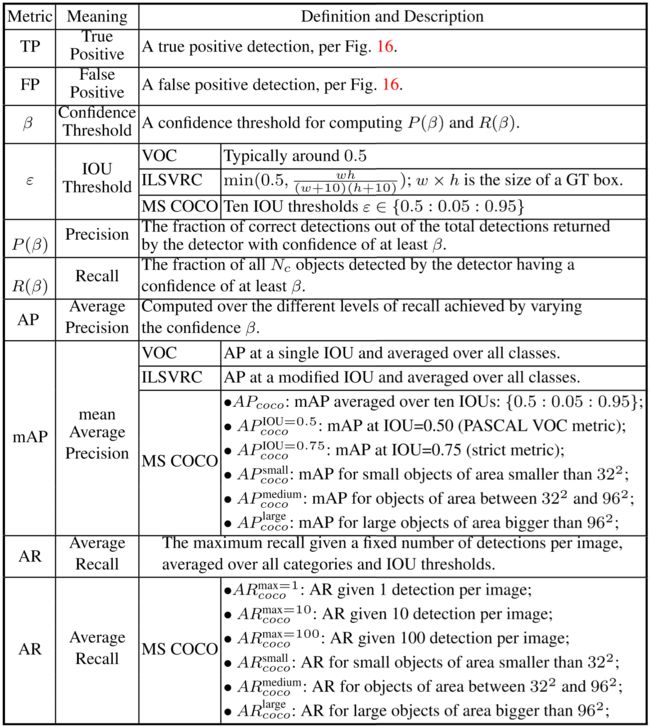
下表展示几个比较有名的网络的性能比较:
| Detector | VOC07 (mAP@IoU=0.5) | VOC12 (mAP@IoU=0.5) | COCO (mAP@IoU=0.5:0.95) | Published In |
|---|---|---|---|---|
| R-CNN | 58.5 | - | - | CVPR’14 |
| SPP-Net | 59.2 | - | - | ECCV’14 |
| Fast R-CNN | 70.0 (07+12) | 68.4 (07++12) | 19.7 | ICCV’15 |
| Faster R-CNN | 73.2 (07+12) | 70.4 (07++12) | 21.9 | NIPS’15 |
| YOLO v1 | 66.4 (07+12) | 57.9 (07++12) | - | CVPR’16 |
| SSD | 76.8 (07+12) | 74.9 (07++12) | 31.2 | ECCV’16 |
| YOLO v2 | 78.6 (07+12) | 73.4 (07++12) | - | CVPR’17 |
| RetinaNet | - | - | 39.1 | ICCV’17 |
| YOLO v3 | - | - | 33.0 | arXiv’18 |
| RefineDet | 83.8 (07+12) | 83.5 (07++12) | 41.8 | CVPR’18 |
| Libra R-CNN | - | - | 43.0 | CVPR’19 |
| Reasoning-RCNN | 82.5 (07++12) | - | 43.2 | CVPR’19 |
| AmoebaNet + NAS-FPN | - | - | 47.0 | CVPR’19 |
| Cascade-RetinaNet | - | - | 41.1 | CVPR’19 |
| AmoebaNet + NAS-FPN + AA | - | - | 50.7 | arXiv’19 |
| EfficientDet | - | - | 51.0 | arXiv’19 |
虽然目标检测的方法分为One-Stage、Two-Stage两种,但是个人感觉不断发展的过程中One-Stage方法的缺点不断的改进,速度以及精度都慢慢超过Two-Stage的方法。所以在一些项目中,采用One-Stage方法已成必然。
注意:本节所有图片截取自论文 ☛ https://arxiv.org/pdf/1809.02165v1.pdf。
[论文解读]
从论文的第一句话就可以看出,作者旨在改善网络的效率,实现更少的参数计算量达到更高的精度。目标检测离不开特征提取,同样图像分类也离不开特征提取。近几年,在图像分类领域,ResNext和EfficientNet打的水深火热,ResNext虽然有较好的精度但是刷新的模型的大小,模型保存参数达到1G以上,而EfficientNet利用AutoML的方法搜索出适合的网络结构实现更高的效率,由此作者提出了两种创新点,并开发一个新的目标检测家族EfficientDet。
说到EfficientDet绕不开EfficientNet,具体可以参照[轻量化卷积神经网络]最后的EfficientNet部分。目前EfficientNet已经出到EfficientNet_b8,在ImageNet上达到 85.37的Top-1精度。
注意:本节所有图片截取自论文 ☛ https://arxiv.org/abs/1911.09070。
[EfficientDet的效率]
作者的目标就是要解决一个问题:Is it possible to build a scalable detection architecture with both higher accuracy and better efficiency across a wide spectrum of resource constraints (e.g., from 3B to 300B FLOPS)? 是否有可能建立一个可扩展的检测体系结构,在广泛的资源限制范围内(例如,从3B到300B的FLOPS)同时具有更高的精确度和更好的效率?针对这个问题作者提出其面临啊的两个巨大挑战:
①有效的多尺度特征融合
之前的研究在多尺度特征融合上只是进行简单的求和,没有考虑不同分辨率具有不同程度的贡献。这里作者提出了一种简单而高效的加权双向特征金字塔网络(BiFPN)。
②模型缩放
之前的研究主要依赖于更大的backbone,例如Faster R-CNN、NAS-FPN,或更大分辨率的输入图像,例如Mask R-CNN,以获得更高的精度。在兼顾精度和效率的情况下,放大特征网络和bounding box和类别预测网络也是至关重要的。在EfficientNet的启发下,作者提出了一种目标检测器的复合标度方法,该方法联合提高了所有backbone、特征网络、bounding box和类别预测网络的分辨率、深度、宽度。这里可以联想到EfficientNet的创新点,改变网络的分辨率、深度、宽度不断生成新的网络,通过AutoML进行结构搜索,找到效率最高的网络结构,从小到大生成b0-b8九种网络结构。作者就是利用这种方法同样生成EfficiebtDet家族网络。
一上来作者展示了EfficiebtDet在效率上的卓越性能,对于一直只用YOLO v3小白的我大吃一惊,如下所示:

图中EfficiebtDet-D0与YOLO v3在性能上不相上下,但是计算量却是YOLO v3的1/30。在EfficiebtDet家族中,EfficiebtDet在相同精度的其他网络的对比中,计算量都远远小于其他的网络,作者在效率上取得的提升十分巨大!不知道能不能在Nano上跑,如果可以的话肯定完虐YOLOv3_tiny。
[双向特征金字塔网络]
对于目标检测网络,由于目标大小的不同,对于不同分辨率的特征图的利用成为重点,给定一个多尺度输入特征列表 P ⃗ i n = ( P l 1 i n , P l 2 i n , … ) \vec{P}^{i n}=\left(P_{l_{1}}^{i n}, P_{l_{2}}^{i n}, \dots\right) Pin=(Pl1in,Pl2in,…),其中 P l i i n P_{l_{i}}^{in} Pliin表示第 l i l_{i} li级别特征,要找到一个变换 f f f使得 P ⃗ o u t = f ( P ⃗ i n ) \vec{P}^{out}=f(\vec{P}^{in}) Pout=f(Pin),这样 P ⃗ o u t \vec{P}^{out} Pout就会聚合不同特征形成新的特征图,以下作者展示了之前比较有代表的特征网络设计方案。(图中每一个箭头代表一个特征图,圆形节点代表卷积操作,某一节点的输入是所有指向该节点的和,从某一节点引出的输出箭头都是一样的)
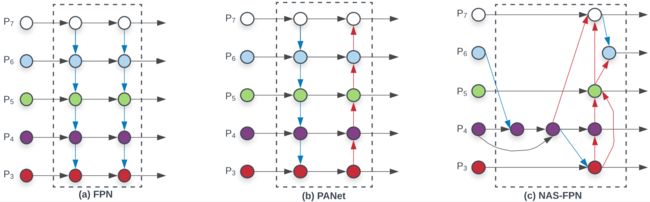
(a)为FPN的结构,假设输入为 P ⃗ i n = ( P 3 i n , P 4 i n , … , P 7 i n ) \vec{P}^{i n}=(P_{3}^{i n}, P_{4}^{i n}, \dots ,P_{7}^{in}) Pin=(P3in,P4in,…,P7in),其分辨率为输入图像的 1 / 2 i 1/2^i 1/2i倍,例如输入为640×640的图像, P ⃗ 3 i n \vec{P}^{in}_3 P3in为 ( 640 / 2 3 ) × ( 640 / 2 3 ) (640/2^3)×(640/2^3) (640/23)×(640/23),传统的FPN就是从上向下聚合多尺度特征图: P 7 o u t = Conv ( P 7 i n ) P 6 o u t = Conv ( P 6 i n + Resize ( P 7 o u t ) ) P 3 o u t = Conv ( P 3 i n + Resize ( P 4 o u t ) ) \begin{aligned} &P_{7}^{o u t}=\operatorname{Conv}\left(P_{7}^{i n}\right)\\ &P_{6}^{o u t}=\operatorname{Conv}\left(P_{6}^{i n}+\operatorname{Resize}\left(P_{7}^{o u t}\right)\right)\\ &P_{3}^{o u t}=\operatorname{Conv}\left(P_{3}^{i n}+\operatorname{Resize}\left(P_{4}^{o u t}\right)\right) \end{aligned} P7out=Conv(P7in)P6out=Conv(P6in+Resize(P7out))P3out=Conv(P3in+Resize(P4out))公式中Resize为上采样或者下采样,使得逐像素求和的特征分辨率相通。
这种(a)的特征网络会受到单向信息的限制,所以在PANet中添加从下向上的结构,如图(b)。而在最近的NAS-FPN则是采用架构搜索获得更好的特征网络,经过大量的计算后会发现网络的结构是不规则的,如图©所示。
[结构方面]
作者在结构做了三种改进进行对比,如下图所示:

(d)为将所有的输入与下一层进行全连接这样会带来巨大的计算量,(e)为针对PANet的改进,作者删掉了只有一个输入的节点,认为这些节点对特征的贡献较少,在(b)中删掉的节点为第一行第二列的节点和第五行第三列的节点,作者将第五行第二列的节点平移到第五行第三列位置,这样就生成简单化的PANet结构。最后(f)就是作者提出的双向特征金字塔网络也就是bidirectional feature pyramid network(BiFPN)。就像ResNet那样对于每层输入增加了一个直连通路。
[融合方面]
对于之前的网络来说,融合不同分辨率的多个特征图时,常见的方法是首先将它们Resize到相同的分辨率,然后对它们进行逐像素求和。但是不同的分辨率往往会提供不同的贡献,所以作者对特征融合进行改进。
①无限取值的融合 O = ∑ i w i ⋅ I i O=\sum_{i} w_{i} \cdot I_{i} O=i∑wi⋅Ii 其中 w i w_{i} wi可以是一组标量对应每个特征图,也可以是一组向量对应每个通道,也可以是一组多维张量对应每个像素值。由于标量权重取值是无限的,可能会导致训练的不稳定性。因此使用权重规范化来限定每个权重的值范围。
②基于Softmax的融合 O = ∑ i e w i ∑ j e w j ⋅ I i O=\sum_{i} \frac{e^{w_{i}}}{\sum_{j} e^{w_{j}}} \cdot I_{i} O=i∑∑jewjewi⋅Ii 另外一个是对每个权重应用softmax,这样所有的权重都被规范化为一个概率值范围从0到1,表示每个输入的重要性。但是额外的softmax会导致GPU硬件显著减速。
③快速归一化融合 O = ∑ i w i ϵ + ∑ j w j ⋅ I i O=\sum_{i} \frac{w_{i}}{\epsilon+\sum_{j} w_{j}} \cdot I_{i} O=i∑ϵ+∑jwjwi⋅Ii 其中,通过在每个 w i w_i wi之后应用ReLU来确保 w i ≥ 0 w_i≥0 wi≥0,并且 ϵ = 0.0001 \epsilon=0.0001 ϵ=0.0001是一个小值,以避免数值不稳定性。类似地,每个标准化权重的值也在0到1之间,但是由于这里没有softmax操作,因此它更为有效。这种快速融合方法与基于softmax的融合具有相似准确性,但在GPU上运行速度高达30%。
作者描述了(f)中所示的BiFPN在6级的两个融合特征: P 6 t d = Conv ( w 1 ⋅ P 6 i n + w 2 ⋅ Resize ( P 7 i n ) w 1 + w 2 + ϵ ) P 6 o u t = Conv ( w 1 ′ ⋅ P 6 i n + w 2 ′ ⋅ P 6 t d + w 3 ′ ⋅ Resize ( P 5 o u t ) w 1 ′ + w 2 ′ + w 3 ′ + ϵ ) \begin{aligned} P_{6}^{t d} &=\operatorname{Conv}\left(\frac{w_{1} \cdot P_{6}^{i n}+w_{2} \cdot \operatorname{Resize}\left(P_{7}^{i n}\right)}{w_{1}+w_{2}+\epsilon}\right) \\ P_{6}^{o u t} &=\operatorname{Conv}\left(\frac{w_{1}^{\prime} \cdot P_{6}^{i n}+w_{2}^{\prime} \cdot P_{6}^{t d}+w_{3}^{\prime} \cdot \operatorname{Resize}\left(P_{5}^{o u t}\right)}{w_{1}^{\prime}+w_{2}^{\prime}+w_{3}^{\prime}+\epsilon}\right) \end{aligned} P6tdP6out=Conv(w1+w2+ϵw1⋅P6in+w2⋅Resize(P7in))=Conv(w1′+w2′+w3′+ϵw1′⋅P6in+w2′⋅P6td+w3′⋅Resize(P5out)) 其中, P 6 t d P^{td}_6 P6td是自上而下路径6级的中间特征, P 6 o u t P^{out}_6 P6out是自下而上路径6级的输出特征。所有其他特征都以类似的方式构建。值得注意的是,为了进一步提高效率,作者使用了可分离的深度卷积进行特征融合,并在每次卷积后添加了批量规范化和激活。
[EfficientDet]
[EfficientDet结构]
下图展示了EfficientDet的结构,符合One-Stage目标检测网络。采用ImageNet预训练网络作为backbone,并从backbone中提取3-7级的特征图 { P 3 , P 4 , P 5 , P 6 , P 7 } \{P_3,P_4,P_5,P_6,P_7\} {P3,P4,P5,P6,P7},将其送入BiFPN中,并反复应用自上向下和自下而上的双向特征融合。这些融合后的特征分别送入bounding box预测网络和类别预测网络中。
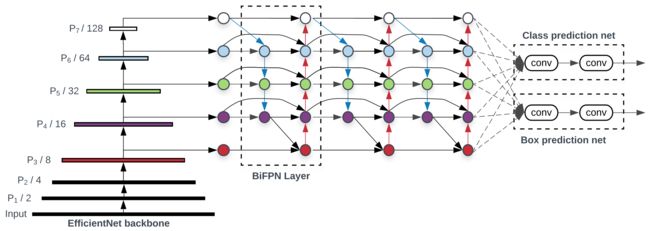
[复合标度]
之前目标检测网络的提升主要是通过使用更大的backbone(例如ResNeXt)、使用更大的输入图像或堆叠更多的FPN层。
在EfficientNet中通过网络的宽度、深度和输入分辨率定义网络的结构,通过复合参数 ϕ ϕ ϕ统一改变网络的三个维度,最终EfficientNet取得了很好的效果。根据EfficientNet,作者提出了一种新的目标检测的复合尺度方法,同样通过复合系数 ϕ ϕ ϕ来统一改变backbone、BiFPN、分类网络、bounding box预测网络和分辨率的所有维度。与EfficientNet不同的是,目标检测器的尺度维数比图像分类模型要大得多,因此对所有维度的网格搜索代价高昂。作者对于每一部分采用另外的方法进行计算:
①backbone
在backbone上,作者采用EfficientNet,如果 ϕ = 0 ϕ=0 ϕ=0则采用EfficientNet_B0作为backbone,如果 ϕ = 6 ϕ=6 ϕ=6则采用EfficientNet_B6作为backbone。
②BiFPN
在BiFPN上,采用以下公式来改变网络的结构, W b i f p n W_{b i f p n} Wbifpn为BiFPN的宽度, D b i f p n D_{b i f p n} Dbifpn为BiFPN网络的深度,通过 ϕ ϕ ϕ调节BiFPN网络的结构。 W b i f p n = 64 ⋅ ( 1.3 5 ϕ ) , D b i f p n = 2 + ϕ W_{b i f p n}=64 \cdot\left(1.35^{\phi}\right), \quad D_{b i f p n}=2+\phi Wbifpn=64⋅(1.35ϕ),Dbifpn=2+ϕ
③分类网络和bounding box预测网络
作者将指定分类网络和bounding box预测网络的宽度始终与BiFPN相同(即 W p r e d = W b i f p n W_{pred}=W_{bifpn} Wpred=Wbifpn),使用公式: D b o x = D c l a s s = 3 + ⌊ ϕ / 3 ⌋ D_{b o x}=D_{c l a s s}=3+\lfloor\phi / 3\rfloor Dbox=Dclass=3+⌊ϕ/3⌋
④输入图像的分辨率
由于将3-7级的特征图输入BiFPN,因此输入分辨率必须可除以 2 7 = 128 2^7=128 27=128,因此使用公式线性增加分辨率: R i n p u t = 512 + 128 × ϕ R_{input}=512+128×ϕ Rinput=512+128×ϕ
下表就是作者设计的EfficientDet家族网络的结构参数:
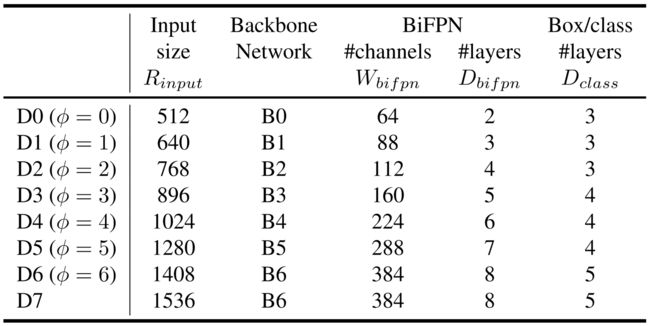
至于作者为什么在EfficientDet_D7采用EfficientNet_B6作为backbone,好像是因为,EfficientNet_B7过大导致网络训练时的BatchSize等不能与其他家族的网络相同,所以作者保留了EfficientDet_D7的其他结构,只改变了backbone为EfficientNet_B6。
[代码解析]
注意:本节所有代码取自非官方项目。
首先,作者在加载backbone之后,将输入图像送入backbone中,得到输入到BiFPN的特征图。在efficientnet.py中,可以得出输入BiFPN的特征集合 { P 3 , P 4 , P 5 , P 6 , P 7 } \{P_3,P_4,P_5,P_6,P_7\} {P3,P4,P5,P6,P7}分别取自backbone的哪一层结构中,如下表所示,展示了EfficientDet_D0-D4的信息。实际上,作者在backbone中获取 { P 1 , P 2 , P 3 , P 4 , P 5 , P 6 , P 7 } \{P_1,P_2,P_3,P_4,P_5,P_6,P_7\} {P1,P2,P3,P4,P5,P6,P7},然后将后5级的特征送入BiFPN中。下表中的数据是取自backbone的第某block/对应特征图的shape/BiFPN输出的shape。
| EfficientDet_D0 | EfficientDet_D1 | EfficientDet_D2 | EfficientDet_D3 | EfficientDet_D4 | |
|---|---|---|---|---|---|
| backbone | EfficientNet_B0 | EfficientNet_B1 | EfficientNet_B2 | EfficientNet_B3 | EfficientNet_B4 |
| input | [ 3 , 512 , 512 ] [3,512,512] [3,512,512] | [ 3 , 640 , 640 ] [3,640,640] [3,640,640] | [ 3 , 768 , 768 ] [3,768,768] [3,768,768] | [ 3 , 896 , 896 ] [3,896,896] [3,896,896] | [ 3 , 1024 , 1024 ] [3,1024,1024] [3,1024,1024] |
| P 1 P_1 P1 | 0 / [ 16 , 256 , 256 ] 0/[16, 256, 256] 0/[16,256,256] / − /- /− | 1 / [ 16 , 320 , 320 ] 1/[16, 320, 320] 1/[16,320,320] / − /- /− | 1 / [ 16 , 384 , 384 ] 1/[16, 384, 384] 1/[16,384,384] / − /- /− | 1 / [ 24 , 448 , 448 ] 1/[24, 448, 448] 1/[24,448,448] / − /- /− | 1 / [ 24 , 512 , 512 ] 1/[24, 512, 512] 1/[24,512,512] / − /- /− |
| P 2 P_2 P2 | 2 / [ 24 , 128 , 128 ] 2/[24, 128, 128] 2/[24,128,128] / − /- /− | 4 / [ 24 , 160 , 160 ] 4/[24, 160, 160] 4/[24,160,160] / − /- /− | 4 / [ 24 , 192 , 192 ] 4/[24, 192, 192] 4/[24,192,192] / − /- /− | 4 / [ 32 , 224 , 224 ] 4/[32, 224, 224] 4/[32,224,224] / − /- /− | 5 / [ 32 , 256 , 256 ] 5/[32, 256, 256] 5/[32,256,256] / − /- /− |
| P 3 P_3 P3 | 4 / [ 40 , 64 , 64 ] 4/[40, 64, 64] 4/[40,64,64] / [ 64 , 64 , 64 ] /[64, 64, 64] /[64,64,64] | 7 / [ 40 , 80 , 80 ] 7/[40, 80, 80] 7/[40,80,80] / [ 88 , 80 , 80 ] /[88, 80, 80] /[88,80,80] | 7 / [ 48 , 96 , 96 ] 7/[48, 96, 96] 7/[48,96,96] / [ 112 , 96 , 96 ] /[112, 96, 96] /[112,96,96] | 7 / [ 48 , 112 , 112 ] 7/[48, 112, 112] 7/[48,112,112] / [ 160 , 112 , 112 ] /[160, 112, 112] /[160,112,112] | 9 / [ 56 , 128 , 128 ] 9/[56, 128, 128] 9/[56,128,128] / [ 224 , 128 , 128 ] /[224, 128, 128] /[224,128,128] |
| P 4 P_4 P4 | 7 / [ 80 , 32 , 32 ] 7/[80, 32, 32] 7/[80,32,32] / [ 64 , 32 , 32 ] /[64, 32, 32] /[64,32,32] | 11 / [ 80 , 40 , 40 ] 11/[80, 40, 40] 11/[80,40,40] / [ 88 , 40 , 40 ] /[88, 40, 40] /[88,40,40] | 11 / [ 88 , 48 , 48 ] 11/[88, 48, 48] 11/[88,48,48] / [ 112 , 48 , 48 ] /[112, 48, 48] /[112,48,48] | 12 / [ 96 , 56 , 56 ] 12/[96, 56, 56] 12/[96,56,56] / [ 160 , 56 , 56 ] /[160, 56, 56] /[160,56,56] | 15 / [ 112 , 64 , 64 ] 15/[112, 64, 64] 15/[112,64,64] / [ 224 , 64 , 64 ] /[224, 64, 64] /[224,64,64] |
| P 5 P_5 P5 | 10 / [ 112 , 16 , 16 ] 10/[112, 16, 16] 10/[112,16,16] / [ 64 , 16 , 16 ] /[64, 16, 16] /[64,16,16] | 15 / [ 112 , 20 , 20 ] 15/[112, 20, 20] 15/[112,20,20] / [ 88 , 20 , 20 ] /[88, 20, 20] /[88,20,20] | 15 / [ 120 , 24 , 24 ] 15/[120, 24, 24] 15/[120,24,24] / [ 112 , 24 , 24 ] /[112, 24, 24] /[112,24,24] | 17 / [ 136 , 28 , 28 ] 17/[136, 28, 28] 17/[136,28,28] / [ 160 , 28 , 28 ] /[160, 28, 28] /[160,28,28] | 21 / [ 160 , 32 , 32 ] 21/[160, 32, 32] 21/[160,32,32] / [ 224 , 32 , 32 ] /[224, 32, 32] /[224,32,32] |
| P 6 P_6 P6 | 14 / [ 192 , 8 , 8 ] 14/[192, 8, 8] 14/[192,8,8] / [ 64 , 8 , 8 ] /[64, 8, 8] /[64,8,8] | 20 / [ 192 , 10 , 10 ] 20/[192, 10, 10] 20/[192,10,10] / [ 88 , 10 , 10 ] /[88, 10, 10] /[88,10,10] | 20 / [ 208 , 12 , 12 ] 20/[208, 12, 12] 20/[208,12,12] / [ 112 , 12 , 12 ] /[112, 12, 12] /[112,12,12] | 23 / [ 232 , 14 , 14 ] 23/[232, 14, 14] 23/[232,14,14] / [ 160 , 14 , 14 ] /[160, 14, 14] /[160,14,14] | 29 / [ 272 , 16 , 16 ] 29/[272, 16, 16] 29/[272,16,16] / [ 224 , 16 , 16 ] /[224, 16, 16] /[224,16,16] |
| P 7 P_7 P7 | 15 / [ 320 , 4 , 4 ] 15/[320, 4, 4] 15/[320,4,4] / [ 64 , 4 , 4 ] /[64, 4, 4] /[64,4,4] | 22 / [ 320 , 5 , 5 ] 22/[320, 5, 5] 22/[320,5,5] / [ 88 , 5 , 5 ] /[88, 5, 5] /[88,5,5] | 22 / [ 352 , 6 , 6 ] 22/[352, 6, 6] 22/[352,6,6] / [ 112 , 6 , 6 ] /[112,6,6] /[112,6,6] | 25 / [ 384 , 7 , 7 ] 25/[384, 7, 7] 25/[384,7,7] / [ 160 , 7 , 7 ] /[160, 7, 7] /[160,7,7] | 31 / [ 448 , 8 , 8 ] 31/[448, 8, 8] 31/[448,8,8] / [ 224 , 8 , 8 ] /[224, 8, 8] /[224,8,8] |
从上表可以看出 W b i f p n W_{b i f p n} Wbifpn实际上对应BiFPN输出的通道数。 D b i f p n D_{b i f p n} Dbifpn代表BiFPN的深度/层数,其中stack=D_bifpn:
for ii in range(stack):
self.stack_bifpn_convs.append(BiFPNModule(channels=out_channels,
levels=self.backbone_end_level-self.start_level,
conv_cfg=conv_cfg,
norm_cfg=norm_cfg,
activation=activation))
如下图所示从左到右为EfficientDet_D0-D4的BiFPN:


在BiFPN的前面还有一层1×1的卷积层,将输入的特征图的通道变为 W b i f p n W_{b i f p n} Wbifpn,从初始级别到最高的级别,也就是3-7共5级,都会有一个1×1的卷积层。
for i in range(self.start_level, self.backbone_end_level):
l_conv = ConvModule(
in_channels[i],
out_channels,
1,
conv_cfg=conv_cfg,
norm_cfg=norm_cfg if not self.no_norm_on_lateral else None,
activation=self.activation,
inplace=False)
self.lateral_convs.append(l_conv)
紧接着,从BiFPN输出的特征图会输入到分类网络和bounding box预测网络,这里采用的是[RetinaNet]中的部分网络。其中假设num_classes=80。
self.bbox_head = RetinaHead(num_classes=num_classes,
in_channels=W_bifpn)
之后其他的anchors的参数:
anchor_scales=[8, 16, 32],
anchor_ratios=[0.5, 1.0, 2.0],
anchor_strides=[4, 8, 16, 32, 64],
num_anchors = len(self.anchor_ratios) * len(self.anchor_scales)
这样可以得出每一个像素都会生成9个anchors:
| EfficientDet_D0 | EfficientDet_D1 | EfficientDet_D2 | EfficientDet_D3 | EfficientDet_D4 | |
|---|---|---|---|---|---|
| P 3 P_3 P3 | [ 64 , 64 , 64 ] [64, 64, 64] [64,64,64] | [ 88 , 80 , 80 ] [88, 80, 80] [88,80,80] | [ 112 , 96 , 96 ] [112, 96, 96] [112,96,96] | [ 160 , 112 , 112 ] [160, 112, 112] [160,112,112] | [ 224 , 128 , 128 ] [224, 128, 128] [224,128,128] |
| P 3 c l s _ s c o r e P_3\ cls\_score P3 cls_score | [ 36864 , 80 ] [36864,80] [36864,80] | [ 57600 , 80 ] [57600,80] [57600,80] | [ 82944 , 80 ] [82944, 80] [82944,80] | [ 112896 , 80 ] [112896, 80] [112896,80] | [ 147456 , 80 ] [147456,80] [147456,80] |
| P 3 b b o x _ p r e d P_3\ bbox\_pred P3 bbox_pred | [ 36864 , 4 ] [36864,4] [36864,4] | [ 57600 , 4 ] [57600,4] [57600,4] | [ 82944 , 4 ] [82944,4] [82944,4] | [ 112896 , 4 ] [112896,4] [112896,4] | [ 147456 , 80 ] [147456,80] [147456,80] |
| P 4 P_4 P4 | [ 64 , 32 , 32 ] [64, 32, 32] [64,32,32] | [ 88 , 40 , 40 ] [88, 40, 40] [88,40,40] | [ 112 , 48 , 48 ] [112, 48, 48] [112,48,48] | [ 160 , 56 , 56 ] [160, 56, 56] [160,56,56] | [ 224 , 64 , 64 ] [224, 64, 64] [224,64,64] |
| P 4 c l s _ s c o r e P_4\ cls\_score P4 cls_score | [ 9216 , 80 ] [9216,80] [9216,80] | [ 14400 , 80 ] [14400,80] [14400,80] | [ 20736 , 80 ] [20736, 80] [20736,80] | [ 28224 , 80 ] [28224, 80] [28224,80] | [ 36864 , 80 ] [36864,80] [36864,80] |
| P 4 b b o x _ p r e d P_4\ bbox\_pred P4 bbox_pred | [ 9216 , 4 ] [9216,4] [9216,4] | [ 14400 , 4 ] [14400,4] [14400,4] | [ 20736 , 4 ] [20736,4] [20736,4] | [ 28224 , 4 ] [28224,4] [28224,4] | [ 36864 , 80 ] [36864,80] [36864,80] |
| P 5 P_5 P5 | [ 64 , 16 , 16 ] [64, 16, 16] [64,16,16] | [ 88 , 20 , 20 ] [88, 20, 20] [88,20,20] | [ 112 , 24 , 24 ] [112, 24, 24] [112,24,24] | [ 160 , 28 , 28 ] [160, 28, 28] [160,28,28] | [ 224 , 32 , 32 ] [224, 32, 32] [224,32,32] |
| P 5 c l s _ s c o r e P_5\ cls\_score P5 cls_score | [ 2304 , 80 ] [2304,80] [2304,80] | [ 3600 , 80 ] [3600,80] [3600,80] | [ 5184 , 80 ] [5184, 80] [5184,80] | [ 7056 , 80 ] [7056, 80] [7056,80] | [ 9216 , 80 ] [9216,80] [9216,80] |
| P 5 b b o x _ p r e d P_5\ bbox\_pred P5 bbox_pred | [ 2304 , 4 ] [2304,4] [2304,4] | [ 3600 , 4 ] [3600,4] [3600,4] | [ 5184 , 4 ] [5184,4] [5184,4] | [ 7056 , 4 ] [7056,4] [7056,4] | [ 9216 , 80 ] [9216,80] [9216,80] |
| P 6 P_6 P6 | [ 64 , 8 , 8 ] [64, 8, 8] [64,8,8] | [ 88 , 10 , 10 ] [88, 10, 10] [88,10,10] | [ 112 , 12 , 12 ] [112, 12, 12] [112,12,12] | [ 160 , 14 , 14 ] [160, 14, 14] [160,14,14] | [ 224 , 16 , 16 ] [224, 16, 16] [224,16,16] |
| P 6 c l s _ s c o r e P_6\ cls\_score P6 cls_score | [ 576 , 80 ] [576,80] [576,80] | [ 900 , 80 ] [900,80] [900,80] | [ 1296 , 80 ] [1296, 80] [1296,80] | [ 1764 , 80 ] [1764, 80] [1764,80] | [ 2304 , 80 ] [2304,80] [2304,80] |
| P 6 b b o x _ p r e d P_6\ bbox\_pred P6 bbox_pred | [ 576 , 4 ] [576,4] [576,4] | [ 900 , 4 ] [900,4] [900,4] | [ 1296 , 4 ] [1296,4] [1296,4] | [ 1764 , 4 ] [1764,4] [1764,4] | [ 2304 , 80 ] [2304,80] [2304,80] |
| P 7 P_7 P7 | [ 64 , 4 , 4 ] [64, 4, 4] [64,4,4] | [ 88 , 5 , 5 ] [88, 5, 5] [88,5,5] | [ 112 , 6 , 6 ] [112,6,6] [112,6,6] | [ 160 , 7 , 7 ] [160, 7, 7] [160,7,7] | [ 224 , 8 , 8 ] [224, 8, 8] [224,8,8] |
| P 7 c l s _ s c o r e P_7\ cls\_score P7 cls_score | [ 144 , 80 ] [144,80] [144,80] | [ 225 , 80 ] [225,80] [225,80] | [ 324 , 80 ] [324, 80] [324,80] | [ 441 , 80 ] [441, 80] [441,80] | [ 576 , 80 ] [576,80] [576,80] |
| P 7 b b o x _ p r e d P_7\ bbox\_pred P7 bbox_pred | [ 144 , 4 ] [144,4] [144,4] | [ 225 , 4 ] [225,4] [225,4] | [ 324 , 4 ] [324,4] [324,4] | [ 441 , 4 ] [441,4] [441,4] | [ 576 , 80 ] [576,80] [576,80] |
| a l l _ a n c h e r s all\_anchers all_anchers | 49104 49104 49104 | 76725 76725 76725 | 110484 110484 110484 | 150381 150381 150381 | 196416 196416 196416 |
[实验结果]
[不同目标检测网络之间的对比]
下表是EfficientDet与其他网络效率的对比,作者对其进行分组,精度相似的网络分为一组,可以看出,在精度相似的情况下,计算量和参数量大大减少。
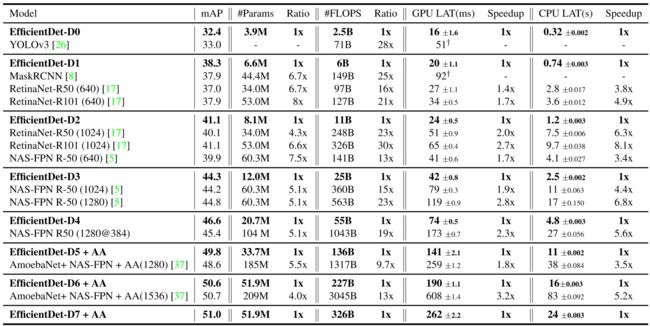
下图展示不同网络之间的在模型大小、GPU推理和CPU推理的对比,也可以看出EfficientDet家族具有很高的效率。

[创新点的对比]
[backbone与BiFPN]
下表展示在不同backbone和特征网络的对比,可以看出,作者的backbone和BiFPN都在效率上有较大的提升。

[不同结构特征网络的对比]
公平起见,作者使用相同的backbone和分类网络和bounding box预测网络,并对所有实验使用相同的训练设置,对于PANet也会对其特征网络叠加5曾与EfficientDet_D3相同。并对比BiFPN是否使用权重进行特征图融合进行对比。

[不同融合特征网络的对比]
在融合方面,之前的FPN是统一分辨率后求和,作者提出增加权重、softmax融合和快速归一化融合的方法,下面是作者做的对比,softmax融合和快速归一化融合最终的效果是下相似的,但是快速归一化融合方法速度要快1.26×~1.31×。

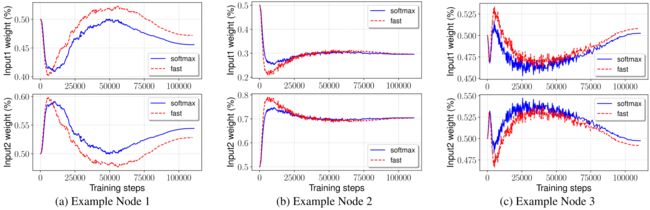
之后作者更进一步观察了两种融合方法的训练过程,下图为在BiFPN随机选取的三个节点,都是具有两个输入,了个输入的权重之和为1,可以看出,不同的输入的贡献是不一样的,而且作者提出的快速归一化融合方法与softmax融合方法训练变化的过程是一样的。
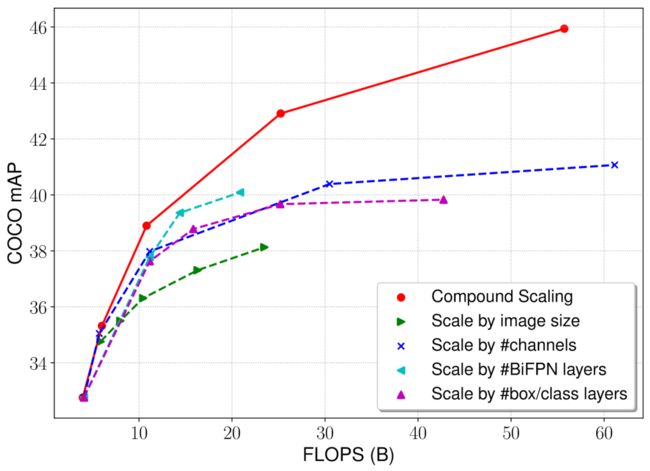
[复合标度的对比]
作者提出利用复合标度改变网络的结构,下图展示了复合标度变化和单一标度变化对网络的影响,可以看出,相比之下复合标度拥有更高的效率。
注意:本节所有图片截取自论文 ☛ https://arxiv.org/abs/1911.09070。