LeetCode相关典型题解合集——动态规划
所有的题型目录在下面的链接
LeetCode相关典型题解合集(两百多道题)
手把手教你做动态规划系列
动态规划框架
一定要明确【状态】和【选择】
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 择优(选择1,选择2...)
动态规划
- 斐波那契数列
-
- 0.斐波那契数列(509)
- 1. 爬楼梯(70)
- 4. 信件错排
- 5. 母牛生产
- 矩阵路径
-
- 1. 矩阵的最小路径和(64)
- 2. 矩阵的总路径数(62)
- 数组区间
-
- 1. 数组区间和(303)
- 2. 数组中等差递增子区间的个数(413)
- 分割整数
-
- 1. 分割整数的最大乘积(343)
- 2. 按平方数来分割整数(279)
- 3. 分割整数构成字母字符串(91)☆
- 子序列问题
-
- 1. 最长递增子序列(300)
- 2. 一组整数对能够构成的最长链(646)
- 3. 最长摆动子序列(376)
- 4. 信封嵌套(354)
- 5. 最长公共子序列(1143)
- 6. 字符串的删除操作(583)
- 7.最小 ASCII 删除和(712)
- 8. 最大子序和(53)
- 背包问题
-
- 0.最基本的背包问题
- 1. 划分数组为和相等的两部分(416)
- 2. 改变一组数的正负号使得它们的和为一给定数(494)
- 3. 01 字符构成最多的字符串(474)
- 4. 找零钱的最少硬币数(322)
- 5. 找零钱的硬币数组合(518)
- 6. 字符串按单词列表分割(139)
- 7. 组合总和(377)
- 股票交易
-
- 1.买卖股票的最佳时机(121)
- 2.买卖股票的最佳时机 II(122)
- 3. 只能进行两次的股票交易(123)
- 4. 只能进行 k 次的股票交易(188)
- 5. 需要冷却期的股票交易(309)
- 6. 需要交易费用的股票交易(714)
- 字符串编辑
-
- 1. 删除两个字符串的字符使它们相等(583)
- 2. 编辑距离(72)
- 3. 复制粘贴字符(650)
- 打家劫舍系列问题
-
- 打家劫舍1(198)
- 打家劫舍2(213)
- 打家劫舍3(337)
- 动态规划其他应用
-
- 鸡蛋掉落887
- 戳气球312
- 石子游戏877
斐波那契数列
0.斐波那契数列(509)
int fib(int n) {
/*//递归 最简单
if(n==0||n==1){
return n;
}
return fib(n-1)+fib(n-2);*/
//动态规划
vector<long> res(n+1,0);
if(n==0||n==1){
return n;
}
res[0]=0;
res[1]=1;
for(int i=2;i<=n;i++){
res[i]=res[i-1]+res[i-2];
}
return res[n];
}
1. 爬楼梯(70)
LeetCode 70. Climbing Stairs (Easy)
注意必须由小于2返回,不然会越界数组
int climbStairs(int n) {
vector<int> dp(n+1);
if(n<=2){
return n;
}
dp[0]=0;
dp[1]=1;
dp[2]=2;
for(int i=3;i<n+1;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
4. 信件错排
LeetCode
5. 母牛生产
LeetCode
矩阵路径
1. 矩阵的最小路径和(64)
LeetCode 64. Minimum Path Sum (Medium)
还是dp
int min(int a,int b){
return a>b?b:a;
}
int minPathSum(vector<vector<int>>& grid) {
int m=grid.size();
int n=grid[0].size();
vector<vector<int>> dp(m+1,vector<int>(n+1));
dp[0][0]=grid[0][0];
for(int i=1;i<m;i++){
dp[i][0]=grid[i][0]+dp[i-1][0];
}
for(int i=1;i<n;i++){
dp[0][i]=grid[0][i]+dp[0][i-1];
}
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j];
}
}
return dp[m-1][n-1];
}
2. 矩阵的总路径数(62)
LeetCode 62. Unique Paths (Medium)
简单的dp,为什么用long 是因为怕数组越界
int uniquePaths(int m, int n) {
vector<vector<long>> dp(m+1,vector<long>(n+1));
for(int i=0;i<m+1;i++){
dp[i][0]=1;
}
for(int i=0;i<n+1;i++){
dp[0][i]=1;
}
for(int i=1;i<m+1;i++){
for(int j=1;j<n+1;j++){
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
数组区间
1. 数组区间和(303)
LeetCode 303. Range Sum Query - Immutable (Easy)
思路:这道题就是个傻逼。因为sumRange函数要调用很多次,因此写的方法不能每次都遍历数组,要用备忘录存着。就是前缀和
vector<int> sum;
NumArray(vector<int>& nums) {
//因为sum数组早于NumArray构造函数,因此无法初始化其值,必须用resize
sum.resize(nums.size()+1);
sum[0]=nums[0];
for(int i=1;i<nums.size();i++){
sum[i]=sum[i-1]+nums[i];
}
}
int sumRange(int left, int right) {
//最简单的是暴力法,每次初始化都遍历计算一次
//这里用备忘录
if(left==0){
return sum[right];
}
return sum[right]-sum[left-1];
}
2. 数组中等差递增子区间的个数(413)
LeetCode 413. Arithmetic Slices (Medium)
思路:写一个函数,用来判断数组i到j是否是等差数列
然后用一个计数器count
bool JudgeFun(vector<int> &nums,int begin,int end){
int temp=nums[begin]-nums[begin+1];
for(int i=begin;i<end;i++){
int judge=nums[i]-nums[i+1];
if(temp!=judge){
return false;
}
}
return true;
}
int numberOfArithmeticSlices(vector<int>& nums) {
int n=nums.size();
int count=0;
vector<vector<int>> dp(n+1,vector<int>(n+1,0));
for(int i=0;i<n-2;i++){
for(int j=i+2;j<n;j++){
if(JudgeFun(nums,i,j)==true){
count++;
}
}
}
return count;
}
分割整数
1. 分割整数的最大乘积(343)
LeetCode 343. Integer Break (Medim)
思路:创建数组dp,其中dp[i] 表示将正整数 i拆分成至少两个正整数的和,这些整数的最大乘积。
当i≥2 时,假设对正整数 i 拆分出的第一个正整数是 j,则有以下两种方案:
- 将 i 拆分成 j 和 i-j的和,且 i-j不再拆分成多个正整数,此时的乘积是 j×(i−j);
- 将 i 拆分成 j 和i−j 的和,且 i−j 继续拆分成多个正整数,此时的乘积是j×dp[i−j]。
详细见官方题解即可
int max(int n,int m){
return n>m?n:m;
}
int integerBreak(int n) {
vector<int> dp(n+1);
//注意题目说n不小于2
for(int i=2;i<n+1;i++){
int Max=0;
for(int j=1;j<i;j++){
//因为有内循环的存在,所以dp[i]会一直变,我们要设一个最大值
Max=max(max(j*(i-j),j*dp[i-j]),Max);
}
dp[i]=Max;
}
return dp[n];
}
2. 按平方数来分割整数(279)
LeetCode 279. Perfect Squares(Medium)
就是完全背包问题!!!
int min(int a,int b){
return a<b?a:b;
}
int numSquares(int n) {
//dp[i]表示能组成i的最小个数
//最多个数就是全为1,因此设置成n+1永远是数组里最大的
vector<int> dp(n+1,n+1);
dp[0]=0;
for(int i=1;i<n+1;i++){
for(int j=1;i-j*j>=0;j++){
dp[i]=min(dp[i],dp[i-j*j]+1);
}
}
return dp[n];
}
3. 分割整数构成字母字符串(91)☆
LeetCode 91. Decode Ways (Medium)
难点: 对 2 个字符,可能解码成 0 种、1 种、2 种情况。所以需要进行分类讨论这2个字符什么时候解码成 0 种,什么时候解码成 1种,什么时候解码成 2种。
解题思路可以看官方的,仔细看能想明白点击这里
这道题妙就妙在解码情况只有两种:只能一个字符串和只能两个字符串,总的解码情况是这两个字符串相加即可。注意一个字符串解码不能为0,两个字符串解码这两个字符串的ascii必须在26之内,包含26
int numDecodings(string s) {
int n=s.size();
vector<int> dp(n+1,0);
//空字符串也可以解码,切记
dp[0]=1;
for(int i=1;i<n+1;i++){
//看一位数解码的情况
if(s[i-1]!='0'){
dp[i]+=dp[i-1];
}
//看两位数解码的情况
//((s[i-2]-'0')*10+(s[i-1]-'0'))<26表示两位数解码必须要在26之内
if(i>1&&s[i-2]!='0'&&((s[i-2]-'0')*10+(s[i-1]-'0'))<=26){
dp[i]+=dp[i-2];
}
}
return dp[n];
}
子序列问题
1. 最长递增子序列(300)
LeetCode 300. Longest Increasing Subsequence (Medium)
思路:动态规划设计:最长递增子序列
int max(int a,int b){
return a>b?a:b;
}
int lengthOfLIS(vector<int>& nums) {
//创建一个dp table 都设置为1,
//最开始第一个肯定为1,因为把自己算进去肯定要
vector<int> dp(nums.size(),1);
for(int i=0;i<nums.size();i++){
for(int j=0;j<i;j++){
if(nums[i]>nums[j]){
dp[i]=max(dp[i],dp[j]+1);
}
}
}
sort(dp.begin(),dp.end());
return dp[nums.size()-1];
}
2. 一组整数对能够构成的最长链(646)
LeetCode 646. Maximum Length of Pair Chain (Medium)
static bool my_function(vector<int> &a,vector<int>&b){
return a[0]<b[0]||(a[0]==b[0]&&a[1]>b[1]);
}
int findLongestChain(vector<vector<int>>& pairs) {
//跟俄罗斯套娃那个题一模一样
sort(pairs.begin(),pairs.end(),my_function);
int n=pairs.size();
vector<int> dp(n,1);
for(int i=0;i<n;i++){
for(int j=0;j<i;j++){
if(pairs[j][1]<pairs[i][0]){
dp[i]=max(dp[i],dp[j]+1);
}
}
}
sort(pairs.begin(),pairs.end());
return dp[n-1];
}
3. 最长摆动子序列(376)
LeetCode 376. Wiggle Subsequence (Medium)
思路:参考链接
int max(int a,int b){
return a>b?a:b;
}
int wiggleMaxLength(vector<int>& nums) {
//最长递增子序列的改进版
//这次要设置两个变量,up和down
//我直接写进阶版,基础班的动态规划在题解里
int n=nums.size();
if(n<2){
return n;
}
int up=1;
int down=1;
for(int i=1;i<n;i++){
if(nums[i]>nums[i-1]){
up=max(up,down+1);
}
else if(nums[i]<nums[i-1]){
down=max(down,up+1);
}
}
return max(up,down);
}
4. 信封嵌套(354)
思路:本质上还是一个最长递增子序列问题
按照w升序,再按照h降序。接着根据h来找最长递增子序列
详细解
static bool my_function(vector<int> &a,vector<int> &b){
return a[0]<b[0]||(a[0]==b[0]&&a[1]>b[1]);
}
int max(int a,int b){
return a>b?a:b;
}
int maxEnvelopes(vector<vector<int>>& envelopes) {
//排序,w升序,然后h降序
sort(envelopes.begin(),envelopes.end(),my_function);
//初始化数组
vector<int> dp(envelopes.size(),1);
for(int i=0;i<envelopes.size();i++){
for(int j=0;j<i;j++){
if(envelopes[i][1]>envelopes[j][1]){
dp[i]=max(dp[i],dp[j]+1);
}
}
}
sort(dp.begin(),dp.end());
return dp[envelopes.size()-1];
}
5. 最长公共子序列(1143)
LeetCode 1143. Longest Common Subsequence
思路:参考链接
int max(int a,int b){
return a>b?a:b;
}
int longestCommonSubsequence(string text1, string text2) {
// 定义:s1[0..i-1] 和 s2[0..j-1] 的 lcs 长度为 dp[i][j]
// 目标:s1[0..m-1] 和 s2[0..n-1] 的 lcs 长度,即 dp[m][n]
// base case: dp[0][..] = dp[..][0] = 0
//为什么要设置0,而不是指针直接从序列的第一个值比较,是因为:
//若是直接从第一个值开始比较,那后面涉及到更新dp table就没有办法用i-1的索引
int m=text1.size();
int n=text2.size();
vector<vector<int>> dp(m+1);
for(int i=0;i<m+1;i++){
dp[i].resize(n+1);
}
//dp[0][..]=0
for(int i=0;i<n+1;i++){
dp[0][i]=0;
}
//dp[..][0] = 0
for(int i=0;i<m+1;i++){
dp[i][0]=0;
}
for(int i=1;i<m+1;i++){
for(int j=1;j<n+1;j++){
if(text1[i-1]==text2[j-1]){
dp[i][j]=1+dp[i-1][j-1];
}else{
//三种情况:、
//①text1不在最长子序列中,则i+1,j不变,继续比较
//②text2不在最长子序列中,则j+1,i不变,继续比较
//③text1和text2都不在,则i+1,j+1,继续比较
//要注意,③情况时包含在①和②的,因为当[j+1,i+1]的最长子序列长度是肯定小于等于[i,j+1]或[i+1,j]
dp[i][j]=max(dp[i][j-1],dp[i-1][j]);
}
}
}
return dp[m][n];
}
另一种写法(推荐)
//另一种写法
int m=text1.size();
int n=text2.size();
vector<vector<int>> dp(m+1,vector<int>(0));
for(int i=0;i<m+1;i++){
dp[i].resize(n+1,0);
}
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(text1[i]==text2[j]){
dp[i+1][j+1]=dp[i][j]+1;
}else{
dp[i+1][j+1]=max(dp[i][j+1],dp[i+1][j]);
}
}
}
return dp[m][n];
}
6. 字符串的删除操作(583)
思路:参考链接
int max(int a,int b){
return a>b?a:b;
}
//本质上还是找最长公共子序列
int minDistance(string word1, string word2) {
int d1=word1.size();
int d2=word2.size();
vector<vector<int>> dp(d1+1);
//dp table是d1+1行,d2+1列
for(int i=0;i<(d1+1);i++){
dp[i].resize(d2+1);
}
//初始化dp table
for(int i=0;i<(d2+1);i++){
dp[0][i]=0;
}
for(int i=0;i<(d1+1);i++){
dp[i][0]=0;
}
//开始更新数组
for(int i=1;i<d1+1;i++){
for(int j=1;j<d2+1;j++){
if(word1[i-1]==word2[j-1]){
dp[i][j]=dp[i-1][j-1]+1;
}else{
dp[i][j]=max(dp[i][j-1],dp[i-1][j]);
}
}
}
int length_seq=dp[d1][d2];
return d1-length_seq+d2-length_seq;
}
7.最小 ASCII 删除和(712)
思路:参考链接
int min(int a,int b){
return a<b?a:b;
}
int max(int a,int b){
return a>b?a:b;
}
int minimumDeleteSum(string s1, string s2) {
//本质上还是最长子序列,不过这次不是个数,而是某个序列值的ASCII码
//①dp table只要计算最大ASCII码,就表示最长子序列,然后总的减去最长的就是答案
//②当相等,什么也不做,若不相等,取最小的ASCII码
int d1=s1.size();
int d2=s2.size();
vector<vector<int>> dp(d1+1,vector<int>(0));
//初始化dp table
for(int i=0;i<d1+1;i++){
dp[i].resize(d2+1,0);
}
//第一种方法
for(int i=0;i<d1;i++){
for(int j=0;j<d2;j++){
if(s1[i]==s2[j]){
dp[i+1][j+1]=dp[i][j]+((int)s1[i]);
}else{
//s1和s2别搞混了
dp[i+1][j+1]=max(dp[i][j+1],dp[i+1][j]);
}
}
}
int sum_ascii=0;
for(int i=0;i<s1.size();i++){
sum_ascii+=(int)s1[i];
}
for(int i=0;i<s2.size();i++){
sum_ascii+=(int)s2[i];
}
return sum_ascii-2*dp[d1][d2];
/*//第二种方法,暂时不会
for(int i=0;i
}
8. 最大子序和(53)
思路:之前贪心好像做过这道题
这次是用动态规划来做
参考链接
//动态规划
//主要在于这个dp table怎么设置的问题
int n=nums.size();
vector<int> dp(n);
dp[0]=nums[0];
for(int i=1;i<n;i++){
dp[i]=max(nums[i],dp[i-1]+nums[i]);
}
sort(dp.begin(),dp.end());
return dp[n-1];
}
背包问题
背包问题
背包问题只有两种东西,一个是target一个是arrs,target就是背包,arrs就是物品
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
0.最基本的背包问题
给你一个可装载重量为W的背包和N个物品,每个物品有重量和价值两个属性。其中第i个物品的重量为wt[i],价值为val[i],现在让你用这个背包装物品,最多能装的价值是多少?
N = 3, W = 4
wt = [2, 1, 3]
val = [4, 2, 3]
#include1. 划分数组为和相等的两部分(416)
LeetCode 416. Partition Equal Subset Sum (Medium)
给一个可装载重量为sum/2的背包和N个物品,每个物品的重量为nums[i]。现在让你装物品,是否存在一种装法,能够恰好将背包装满?
详细解释
最初版本代码
bool canPartition(vector<int>& nums) {
int sum=0;
for(auto a:nums){
sum+=a;
}
if(sum%2!=0){
return false;
}
int goal=sum/2;
int n=nums.size();
//dp[i][j]代表前i个,当背包容量为j的时候的bool函数值
vector<vector<bool>> dp(n+1,vector<bool>(goal+1));
//dp[...][0]肯定是true,因为背包容量为0,肯定一直为true
for(int i=0;i<n+1;i++){
dp[i][0]=true;
}
//dp[0][...]肯定为false,因为如果0个值,无论多少都是false
for(int i=0;i<goal+1;i++){
dp[0][i]=false;
}
//转移状态
//如果不把第i个算进去,则取决于上一个状态dp[i-1][j]
//如果吧第i个算进去,则取决于状态dp[i - 1][j-nums[i-1]]
for(int i=1;i<n+1;i++){
for(int j=1;j<goal+1;j++){
if(j-nums[i-1]<0){
dp[i][j]=dp[i-1][j];
}else{
//看这两种情况哪一种正好能装够goal,如果都没有肯定是false,所以用||
dp[i][j]=dp[i-1][j]||dp[i-1][j-nums[i-1]];
}
}
}
return dp[n][goal];
}
改进代码
//改进的方法
vector<bool> dp(goal+1,false);
dp[0]=true;
for(int i=0;i<n;i++){
//从后往前遍历,每个数字只能用一次
for(int j=goal;j>=0;j--){
if(j-nums[i]>=0){
dp[j]=dp[j]||dp[j-nums[i]];
}
}
}
return dp[goal];
2. 改变一组数的正负号使得它们的和为一给定数(494)
LeetCode 494. Target Sum (Medium)
思路:参考本链接
先将本问题转换为01背包问题。
假设所有符号为+的元素和为x,符号为-的元素和的绝对值是y。
我们想要的 S = 正数和 - 负数和 = x - y
而已知x与y的和是数组总和:x + y = sum
可以求出 x = (S + sum) / 2 = target
也就是我们要从nums数组里选出几个数,令其和为target
于是就转化成了求容量为target的01背包问题 =>要装满容量为target的背包
int findTargetSumWays(vector<int>& nums, int target) {
//第一种解题思路:转换成了01背包为题
int sum=0;
for(auto num:nums){
sum+=num;
}
if(target>sum||(target+sum)%2!=0){
return 0;
}
//求容量为temp的01背包问题
int temp=(target+sum)/2;
vector<int> dp(temp+1);
//dp[j]代表的意义:填满容量为j的背包,有dp[j]种方法。
//填满容量为0的背包有且只有一种
dp[0]=1;
for(auto num:nums){
for(int j=temp;j>=0;j--){
if(j>=num){
dp[j]=dp[j]+dp[j-num];
}else{
dp[j]=dp[j];
}
}
}
return dp[temp];
}
3. 01 字符构成最多的字符串(474)
LeetCode 474. Ones and Zeroes (Medium)
思路:此道题就是01背包,只不过状态不是两个而是三个,其他一模一样
注意:vector如何定义三维数组
int max(int a,int b){
return a>b?a:b;
}
vector<int> count_one_and_zero(string &strs){
vector<int> dp(2,0);
for(int i=0;i<strs.size();i++){
if(strs[i]=='0'){
dp[0]++;
}
else if(strs[i]=='1'){
dp[1]++;
}
}
return dp;
}
int findMaxForm(vector<string>& strs, int m, int n) {
int num=strs.size();
//三维数组的表示方法
vector<vector<vector<int>>> dp(num+1,vector<vector<int>>(m+1,vector<int>(n+1,0)));
for(int i=1;i<num+1;i++){
vector<int> count=count_one_and_zero(strs[i-1]);
int count_zero=count[0];
int count_one=count[1];
for(int j=0;j<m+1;j++){
for(int w=0;w<n+1;w++){
if(j-count_zero>=0&&w-count_one>=0){
dp[i][j][w]=max(dp[i-1][j][w],dp[i-1][j-count_zero][w-count_one]+1);
}else{
dp[i][j][w]=dp[i-1][j][w];
}
}
}
}
return dp[num][m][n];
}
4. 找零钱的最少硬币数(322)
LeetCode 322. Coin Change (Medium)
思路:参考链接
自底向上的迭代写法
int coinChange(vector<int>& coins, int amount) {
//只要不用push_back,则要初始化数组的大小
//数组输出化要设置为最大值,但一般设置为比amount大1即可
vector<int> res (amount+1,amount+1);
//当amount=0时候,硬币数为0
res[0]=0;
for(int i=1;i<=amount;i++){
//遍历不同硬币的集合
for(int j=0;j<coins.size();j++){
if(i>=coins[j]){
res[i]=res[i]>(res[i-coins[j]]+1)?(res[i-coins[j]]+1):res[i];
}
}
}
//当用dp table遍历完整个流程的时候,其实没有考虑能不能凑出amount的硬币
//当凑不出来的时候,根据代码,res[amount]是大于amount的
return res[amount]>amount?-1:res[amount];
}
5. 找零钱的硬币数组合(518)
LeetCode 518. Coin Change 2 (Medium)
思路:点击这里
int change(int amount, vector<int>& coins) {
int n=coins.size();
vector<vector<int>> dp(n+1,vector<int>(amount+1,0));
for(int i=0;i<n+1;i++){
dp[i][0]=1;
}
for(int i=1;i<n+1;i++){
for(int j=1;j<amount+1;j++){
if(j-coins[i-1]>=0){
dp[i][j]=dp[i-1][j]+dp[i][j-coins[i-1]];
}else{
dp[i][j]=dp[i-1][j];
}
}
}
return dp[n][amount];
}
6. 字符串按单词列表分割(139)
LeetCode 139. Word Break (Medium)
思路:
1、这里面有字符串s和单词列表wordDict。我们考虑单词列表中的单词是否可以组成字符表s,按照题意,单词列表是无限选取的,因此我们可以把这一道题规约为完全背包问题。
当这道变成完全背包问题的时候,就可以套用完全背包的公式。首先我们把字符串s看做为背包(target),单词列表看做为arrs,即物品。接着这道题是求排列数而不是组合数(比如说能装的最大价值,这个叫做组合数)。
因此,根据如果求组合数就是外层for循环遍历物品,内层for遍历背包。如果求排列数就是外层for遍历背包,内层for循环遍历物品。我们外层遍历target,内存遍历物品
2、接下来我们要求状态转移方程。
这里面用1维数组即可,表示字符串s前i个字符组成的字符串s[0…i−1]是否能被空格拆分成若干个字典中出现的单词。同时我们要设置一个标志位j,为什么呢?。
首先我们把前i个字符串称为s1,对于s1了来说,物品不管怎么取是否能装满背包(target),则要分段来考虑。可以类比背包为5,有2和3两个物品,如果能装满背包,则要把5分段考虑,分为2和3,如果2和3都能从物品中取,则必然能装满背包。
因此字符串s1也是如此,我们设置一个标志位j。0-j位的字符串用s2表示,j-i-1位的字符串用s3表示。则只有s2和s3都匹配到了单词表中的单词,才能说字符串s1能被单词表中的单词组成
s3就要用函数看是否匹配了,那么s2呢?不用再写一个函数,这也是动态规划的特点,下一个状态和上一个状态有关。s2是前0-j个字符组成的串,而这0-j个字符串是否匹配可以用dp[j]表示!这就是关键!
举个例子:字符串"leetcode",当i=8,j=4的时候,s2=“leet”,s3=“code”,s2是否匹配直接看dp[j]即dp[4],这在前面已经计算过了,而s3是否包含需要用函数计算
因此状态转移方程就是:dp[i]=dp[j]&&find(s3 in 单词列表)
3、注意事项。
首先我们dp数组设置为外层循环的长度+1,即背包长度(target)+1。因为我们求子串的时候,必须要+1才行,可以自己写一下感受一下,不多一位我们求不了完全的子串
其次写状态转移方程不能直接写dp[i]=dp[j]&&find(s3 in 单词列表),我就是这样写结果出错,调试了半天才找到原因。这样写dp[i]在每次内循环中都会更新,而这样的更新是没有意义的,我们只要一次更新就行,因此代码中的写法才是正确的
bool wordBreak(string s, vector<string>& wordDict) {
int s_len=s.size();
//因为vector没有find函数,因此用stl的非序列式容器存储
//用unordered_set而不是unordered_map是因为set的key和value是相等的
unordered_set<string> res;
for(auto word:wordDict){
res.insert(word);
}
//设置dp数组,如果求组合数就是外层for循环遍历物品,内层for遍历背包。
//如果求排列数就是外层for遍历背包,内层for循环遍历物品。
vector<bool> dp(s_len+1,false);
dp[0]=true;
//外层循环是背包
for(int i=1;i<s_len+1;i++){
//内层循环是物品
for(int j=0;j<i;j++){
//状态转移方程
//但是不能这样写,会出错!
//dp[i]=dp[j]&&(res.find(s.substr(j,i-j))!=res.end());
if(dp[j]&&res.find(s.substr(j,i-j))!=res.end()){
dp[i]=true;
break;
}
}
}
return dp[s_len];
}
7. 组合总和(377)
LeetCode 377. Combination Sum IV (Medium)
参考链接
因为这个求排列组合数的,所以物品应该放在外层
int combinationSum4(vector<int>& nums, int target) {
int n_size=nums.size();
vector<int> dp(target+1,0);
dp[0]=1;
for(int i=1;i<target+1;i++){
for(int j=0;j<n_size;j++){
//dp[i]+dp[i-nums[j]]
if(i-nums[j]>=0&&dp[i]<INT_MAX-dp[i-nums[j]]){
dp[i]+=dp[i-nums[j]];
}
}
}
return dp[target];
}
股票交易
团灭股票问题的文章详解
1.买卖股票的最佳时机(121)
正常解法,无套路
//基本的解法
int minPrice=1e9;
int maxProfit=0;
for(auto price:prices){
minPrice=price>minPrice?minPrice:price;
maxProfit=(price-minPrice)>maxProfit?(price-minPrice):maxProfit;
}
return maxProfit;*/
动态规划套路解法
/***********动态规划的解法****************/
//k即买卖次数,这道题里面k为1
int n=prices.size();
//设置dp数组和初始化它
vector<vector<int>> dp(n);
for(int i=0;i<n;i++){
dp[i].resize(2);
}
for(int i=0;i<n;i++){
if(i==0){
dp[i][1]=-prices[i];
dp[i][0]=0;
continue;
}
dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i]);
dp[i][1]=max(dp[i-1][1],-prices[i]);
//为什么不是dp[i-1][0]-prices[i]而是-prices[i]?
//答:因为本质上这里面k=1,而dp[i][1]=max(dp[i-1][1],-prices[i])的全貌是
//dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
//dp[i][1][1] = max(dp[i-1][1][1], dp[i-1][0][0] - prices[i])
//而dp[i-1][0][0]是为0的,也就表明只能交易一次
}
return dp[n-1][0];
}
2.买卖股票的最佳时机 II(122)
简单的版本
int maxProfit(vector<int>& prices) {
int minPrice=1e9;
int maxProfit=0;
for(int i=0;i<prices.size()-1;i++){
if(prices[i]<prices[i+1]){
maxProfit+=prices[i+1]-prices[i];
}
}
return maxProfit;
}
动态规划套路解法
int max(int a,int b){
return a>b?a:b;
}
int maxProfit(vector<int>& prices) {
//注意 这道题目里面k即交易次数是不限制的
int n=prices.size();
vector<vector<int>> dp(n+1);
for(int i=0;i<n;i++){
dp[i].resize(2);
}
for(int i=0;i<n;i++){
if(i==0){
dp[i][0]=0;
dp[i][1]=-prices[i];
continue;
}
dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i]);
//买入卖出不限次数,所以为dp[i-1][0]-prices[i]
dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i]);
}
return dp[n-1][0];
}
3. 只能进行两次的股票交易(123)
LeetCode 123. Best Time to Buy and Sell Stock III (Hard)
只能进行两次的比较特殊。
因为上面的情况都和 k 的关系不太大。
要么 k 是正无穷,状态转移和 k 没关系了;
要么 k = 1,跟 k = 0 这个 base case 挨得近,最后也没有存在感。
这道题 k = 2 和后面要讲的 k 是任意正整数的情况中,对 k 的处理就凸显出来了
这道题切记,k的影响不能消除!!
int max(int a,int b){
return a>b?a:b;
}
int maxProfit(vector<int>& prices) {
int n=prices.size();
//三维数组初始化,注意k为3,不然数组会越界
vector<vector<vector<int>>> dp(n,vector<vector<int>>(3,vector<int>(2)));
for(int i=0;i<n;i++){
for(int k=2;k>0;k--){
if(i==0){
dp[i][k][0]=0;
dp[i][k][1]=-prices[i];
continue;
}
dp[i][k][0]=max(dp[i-1][k][0],dp[i-1][k][1]+prices[i]);
dp[i][k][1]=max(dp[i-1][k][1],dp[i-1][k-1][0]-prices[i]);
}
}
return dp[n-1][2][0];
}
4. 只能进行 k 次的股票交易(188)
LeetCode 188. Best Time to Buy and Sell Stock IV (Hard)
注意!这里面是k次,和之前的2次非常的相似,但是!我们要考虑一种情况:即k如果大于了n/2,可以自己举个例子,这种情况表明对k是没有约束的,这种情况下可以把k看做成为无穷次!
第二!数组可能为0,要注意!
int max(int a,int b){
return a>b?a:b;
}
int maxProfit(int k, vector<int>& prices) {
/*思路:k次,之前有个k=2的*/
int n=prices.size();
//初始化一个三维数组
vector<vector<vector<int>>> dp(n,vector<vector<int>>(k+1,vector<int>(2)));
//注意, k 应该不超过 n/2!!!
//如果k大于了一半,k就没有约束了,我们可以把k看做无穷
if(prices.empty()){
return 0;
}
if(k>(n/2)){
return maxProfit_inf(prices);
}
for(int i=0;i<n;i++){
for(int j=k;j>0;j--){
if(i==0){
dp[i][j][0]=0;
dp[i][j][1]=-prices[i];
continue;
}
dp[i][j][0]=max(dp[i-1][j][0],dp[i-1][j][1]+prices[i]);
dp[i][j][1]=max(dp[i-1][j][1],dp[i-1][j-1][0]-prices[i]);
}
}
return dp[n-1][k][0];
}
int maxProfit_inf(vector<int>& prices){
int n=prices.size();
vector<vector<int>> dp(n,vector<int>(2));
for(int i=0;i<n;i++){
if(i==0){
dp[i][0]=0;
dp[i][1]=-prices[i];
continue;
}
dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i]);
dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i]);
}
return dp[n-1][0];
}
5. 需要冷却期的股票交易(309)
LeetCode 309. Best Time to Buy and Sell Stock with Cooldown(Medium)
这道题也有两种思路
第一种是延续之前高票交易的思路,只不过当卖过股票再买的时候是i-2不是i-1了
第二种是有三种状态,不持有,持有,冷冻期,即dp[n][3]
第一种延续之前的方法
int max(int a,int b){
return a>b?a:b;
}
int maxProfit(vector<int>& prices) {
if(prices.empty()){
return 0;
}
int n=prices.size();
vector<vector<int>> dp(n,vector<int>(2));
for(int i=0;i<n;i++){
if(i==0){
dp[i][0]=0;
dp[i][1]=-prices[i];
continue;
}
if(i==1){
dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i]);
//如果i=1,且手里有股票,表明第二天要么跟前一天没变,要么就是第一次买
dp[i][1]=max(dp[i-1][1],0-prices[i]);
continue;
}
dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i]);
//有冷却期唯一的区别就是不能是前一天交易,而是前两天(i-2)天交易了
dp[i][1]=max(dp[i-1][1],dp[i-2][0]-prices[i]);
}
return dp[n-1][0];
}
第二种方法,三种状态
int max(int a,int b){
return a>b?a:b;
}
int maxProfit(vector<int>& prices) {
if(prices.empty()){
return 0;
}
int n=prices.size();
vector<vector<int>> dp(n,vector<int>(3));
for(int i=0;i<n;i++){
if(i==0){
dp[i][0]=0;
dp[i][1]=-prices[i];
dp[i][2]=0;
continue;
}
dp[i][0]=max(dp[i-1][0],dp[i-1][2]);
//有冷却期唯一的区别就是不能是前一天交易,而是前两天(i-2)天交易了
dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i]);
//如果冷却期就说明前一天卖掉了
dp[i][2]=dp[i-1][1]+prices[i];
}
//比较卖出了和在冷却期的时候那个大
return max(dp[n-1][0],dp[n-1][2]);
}
6. 需要交易费用的股票交易(714)
LeetCode 714. Best Time to Buy and Sell Stock with Transaction Fee (Medium)
int max(int a,int b){
return a>b?a:b;
}
int maxProfit(vector<int>& prices, int fee) {
if(prices.empty()){
return 0;
}
int n=prices.size();
vector<vector<int>> dp(n,vector<int>(2));
for(int i=0;i<n;i++){
if(i==0){
dp[i][0]=0;
dp[i][1]=-prices[i]-fee;
continue;
}
dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i]);
dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i]-fee);
}
return dp[n-1][0];
}
字符串编辑
1. 删除两个字符串的字符使它们相等(583)
LeetCode 583. Delete Operation for Two Strings (Medium)
2. 编辑距离(72)
LeetCode 72. Edit Distance (Hard)
思路:看此链接即可
int min(int a,int b,int c){
int temp=a>b?b:a;
return temp>c?c:temp;
}
int minDistance(string word1, string word2) {
int d1=word1.length();
int d2=word2.length();
//创建dp table
//(d1+1)行,(d2+1)列
vector<vector<int>> dp(d1+1);
for(int i=0;i<(d1+1);i++){
dp[i].resize(d2+1);
}
//初始化这个DP table
//从s1的第0个元素依次到s2的每一个元素,距离递增,为0123....
for(int i=0;i<(d2+1);i++){
dp[0][i]=i;
}
//同理,从s2的第0个元素依次到s1的每一个元素,距离递增,为0123....
for(int i=0;i<(d1+1);i++){
dp[i][0]=i;
}
//用了dp table就要自底向上求解
//行列对应的到底是哪一个字符串的长度要搞清楚!
for(int i=1;i<=d1;i++){
for(int j=1;j<=d2;j++){
if(word1[i-1]==word2[j-1]){
dp[i][j]=dp[i-1][j-1];
}else{
dp[i][j]=min(dp[i-1][j]+1, //删除
dp[i][j-1]+1, //插入
dp[i-1][j-1]+1 //替换
);
}
}
}
return dp[d1][d2];
}
3. 复制粘贴字符(650)
LeetCode 650. 2 Keys Keyboard (Medium)
打家劫舍系列问题
打家劫舍问题看此文章
打家劫舍1(198)
int max(int a,int b){
return a>b?a:b;
}
int rob(vector<int>& nums) {
int n=nums.size();
vector<int> dp(n+1);
dp[0]=0;
dp[1]=nums[0];
for(int i=2;i<n+1;i++){
dp[i]=max(dp[i-1],dp[i-2]+nums[i-1]);
}
return dp[n];
}
打家劫舍2(213)
思路:假设数组nums 的长度为 n。
如果不偷窃最后一间房屋,则偷窃房屋的下标范围是 [0,n−2]。
如果不偷窃第一间房屋,则偷窃房屋的下标范围是 [1,n−1]。
这里面下标指的是数组的下标
在确定偷窃房屋的下标范围之后,即可用第 198 题的方法解决
int rob(vector<int>& nums) {
int n=nums.size();
if(n==1){
return nums[0];
}
else if(n==2){
return max(nums[0],nums[1]);
}else{
return max(basic_rob(nums,1,n-1),basic_rob(nums,2,n));
}
}
int max(int a,int b){
return a>b?a:b;
}
//注意,这里面star和end不是数组下标,而是本身序列
int basic_rob(vector<int>& nums,int start,int end){
vector<int> dp(nums.size());
dp[0]=0;
dp[1]=nums[start-1];
//判断,看属于是偷第一个还是最后一个
//如果偷第一个,则num[i-1]
//如果偷最后一个,则num[i]
if(start==1){
for(int k=2;k<nums.size();k++){
dp[k]=max(dp[k-1],nums[k-1]+dp[k-2]);
}
}else{
for(int k=2;k<nums.size();k++){
dp[k]=max(dp[k-1],nums[k]+dp[k-2]);
}
}
return dp[nums.size()-1];
}
下面这种方法比较粗俗易懂
因为这道题分成两种情况,偷第一间屋子最后一间就不偷,偷最后一间屋子第一间就不偷
因此可以分成两个数组,套用同一个dp函数来做
打家劫舍3(337)
这道题我之前在二叉树的专题写过,但是当时通过了。这次重新用递归却没通过,说超时了,很郁闷。之前递归的思路是选根节点或者不选根节点,一次递归就行,但是由于没有记忆化搜索(记忆化递归),遇到比较复杂的二叉树的时候就会出现问题,报超时错误
源代码
int max(int a,int b){
return a>b?a:b;
}
int rob(TreeNode* root) {
if(root==nullptr){
return 0;
}
if(root->left==nullptr&&root->right==nullptr){
return root->val;
}
//偷父节点
int cash1=root->val;
//不偷父节点
int cash2=0;
if(root->left!=nullptr ){
cash1+=rob(root->left->left)+rob(root->left->right);
cash2+=rob(root->left);
}
if(root->right!=nullptr){
cash1+=rob(root->right->left)+rob(root->right->right);
cash2+=rob(root->right);
}
return max(cash1,cash2);
}
修改上述代码,记忆化递归
int max(int a,int b){
return a>b?a:b;
}
int rob(TreeNode* root) {
//用一个hash结构来当做备忘录
unordered_map<TreeNode*,int> res;
if(root==nullptr){
return 0;
}
/*if(root->left==nullptr&&root->right==nullptr){
return root->val;
}*/
if(res.find(root)!=res.end()){
return res[root];
}
//偷父节点
int cash1=root->val;
//不偷父节点
int cash2=0;
if(root->left!=nullptr ){
cash1+=rob(root->left->left)+rob(root->left->right);
}
if(root->right!=nullptr){
cash1+=rob(root->right->left)+rob(root->right->right);
}
cash2+=rob(root->left)+rob(root->right);
int max_cash= max(cash1,cash2);
res[root]=max_cash;
return max_cash;
}
很不幸,还是超时了!!!
为什么呢??
原因是unordered_map必须放在递归函数外面!不然每次都会重新定义一个哈希表,想不超时都不可能
int max(int a,int b){
return a>b?a:b;
}
//用一个hash结构来当做备忘录
unordered_map<TreeNode*,int> res;
int rob(TreeNode* root) {
if(root==nullptr){
return 0;
}
if(root->left==nullptr&&root->right==nullptr){
return root->val;
}
if(res.find(root)!=res.end()){
return res[root];
}
//偷父节点
int cash1=root->val;
//不偷父节点
int cash2=0;
if(root->left!=nullptr ){
cash1+=rob(root->left->left)+rob(root->left->right);
}
if(root->right!=nullptr){
cash1+=rob(root->right->left)+rob(root->right->right);
}
cash2+=rob(root->left)+rob(root->right);
int max_cash= max(cash1,cash2);
res[root]=max_cash;
return max_cash;
}
动态规划其他应用
鸡蛋掉落887
思路:详细思路参考此链接
在这里我只说大致思路
经典的动态规划框架,状态+选择,然后穷举、
状态很显然就是目前所有的鸡蛋数目k和楼层数N
选择指的是去哪一层楼扔鸡蛋
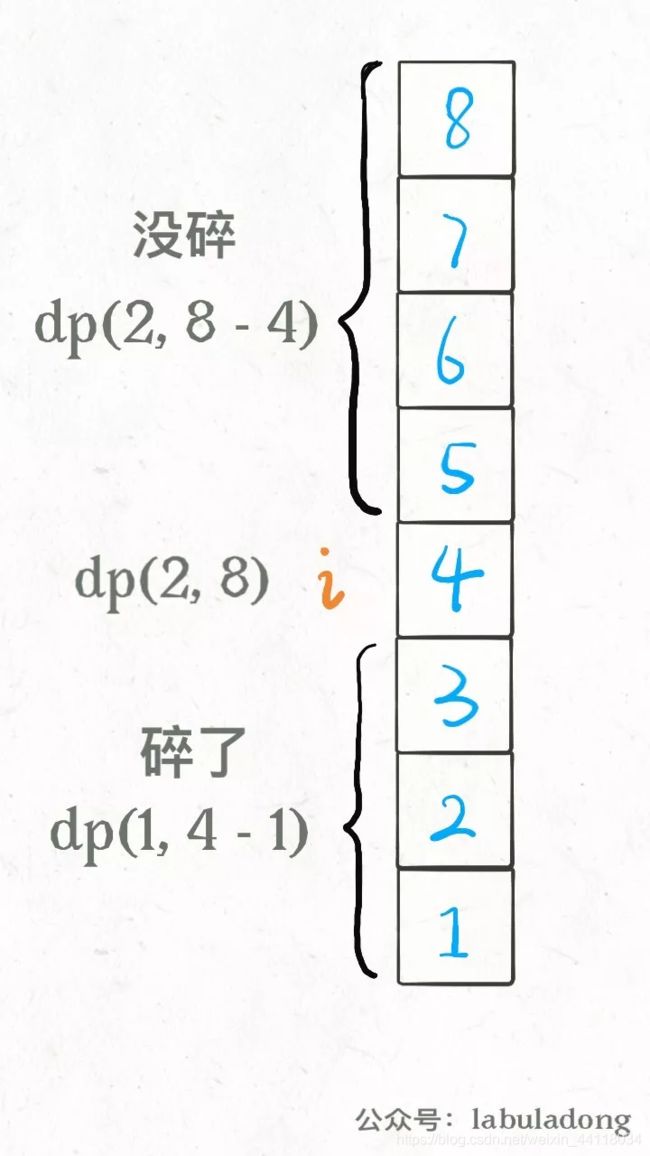
状态转移:①如果鸡蛋碎了,鸡蛋的个数减一,搜索的楼层区间从[1…N]变为[1…i-1]共i-1层楼
②如果鸡蛋没碎,鸡蛋个数不变,搜索的楼层区间应该从 [1…N]变为[i+1…N]共N-i层楼。
int max(int a,int b){
return a>b?a:b;
}
int min(int a,int b){
return a<b?a:b;
}
int superEggDrop(int k, int n) {
int egg=k;
int floor=n;
//dp数组表示表示dp[floor][egg]
vector<vector<int>> dp(floor+1,vector<int>(egg+1,0));
//初始化dp数组
//1层楼,只能扔一次
for(int i=1;i<egg+1;i++){
dp[1][i]=1;
}
//只有1个鸡蛋
for(int i=1;i<floor+1;i++){
dp[i][1]=i;
}
//一层楼1个鸡蛋直接就定义好了
for(int i=2;i<floor+1;i++){
for(int j=2;j<egg+1;j++){
int temp=INT_MAX;
//多了一个循环是因为如果有j个鸡蛋,那么第一个鸡蛋有n种扔法,可以在1-n的任意一层扔
for(int m=1;m<=i;m++){
temp=min(temp,max(dp[m-1][j-1],dp[i-m][j])+1);
}
dp[i][j]=temp;
}
}
return dp[n][k];
}
思路2:“求k个鸡蛋在m步内可以测出多少层”
令dp[k][m]表示k个鸡蛋在m步内可以测出的最多的层数,那么当我们在第X层扔鸡蛋的时候,就有两种情况:
- 鸡蛋碎了,我们少了一颗鸡蛋,也用掉了一步,此时测出N - X + dp[k-1][m-1]层,X和它上面的N-X层已经通过这次扔鸡蛋确定大于F
- 鸡蛋没碎,鸡蛋的数量没有变,但是用掉了一步,剩余X + dp[k][m-1],X层及其以下已经通过这次扔鸡蛋确定不会大于F
也就是说,我们每一次扔鸡蛋,不仅仅确定了下一次扔鸡蛋的楼层的方向,也确定了另一半楼层与F的大小关系,所以在下面的关键代码中,使用的不再是max,而是加法(这里是重点)。评论里有人问到为什么是相加,其实这里有一个惯性思维的误区,上面的诸多解法中,往往求max的思路是“两种方式中较大的那一个结果”,其实这里的相加,不是鸡蛋碎了和没碎两种情况的相加,而是“本次扔之后可能测出来的层数 + 本次扔之前已经测出来的层数”。
关键点在于不管鸡蛋碎不碎,都用掉了一步
同时只要我们测出了所有的层数,就可以返回了!
int superEggDrop(int k, int n) {
vector<vector<int>> dp(k+1,vector<int>(n+1,0));
//dp[j][i]代表j个鸡蛋在i步内可以测试出的层数
//如果层数达到最大层,就返回i步,此数就是最佳值
//0个鸡蛋都是0
for(int i=1;i<n+1;i++){
for(int j=1;j<k+1;j++){
//不管鸡蛋碎不碎,都用掉了一步
dp[j][i]=dp[j][i-1]+dp[j-1][i-1]+1;
//到了最大层就说明至少用了j步
if(dp[j][i]>=n){
return i;
}
}
}
return n;
}
戳气球312
思路:看这个链接即可
int max(int a,int b){
return a>b?a:b;
}
int maxCoins(vector<int>& nums) {
int n=nums.size();
vector<int> temp(n+2);
vector<vector<int>> dp(n+2,vector<int>(n+2));
temp[0]=1;
temp[n+1]=1;
for(int i=1;i<n+1;i++){
temp[i]=nums[i-1];
}
for(int i=n;i>=0;i--){
for(int j=i+1;j<n+2;j++){
for(int k=i+1;k<j;k++){
dp[i][j]=max(dp[i][j],dp[i][k]+dp[k][j]+(temp[i]*temp[j]*temp[k]));
}
}
}
return dp[0][n+1];
}
石子游戏877
思路:看这个链接
先手在做出选择之后,就成了后手,后手在对方做完选择后,就变成了先手。这种角色转换使得我们可以重用之前的结果,典型的动态规划标志。