贝叶斯分层模型（Hierarchical Models）

前言

许多统计应用涉及多个参数，这些参数可以通过问题的结构以某种方式被视为相关或连接，这意味着这些参数的联合概率模型应该反映它们的相关性。例如，在一项关于心脏治疗效果的研究中，由于j医院的患者具有生存概率θj，因此可以合理地预期${\theta }_j$的估计值（代表医院样本）应该相互关联。如果我们使用先验分布，其中${\theta }_j$的估计值被视为普通种群分布的样本，我们将看到这是以自然的方式实现的。这种应用的一个关键特征是，观测到的数据y ij，在以j为索引的组中以i为索引的单位，可以用来估计${\theta }_j$的种群分布，即使${\theta }_j$的值本身没有观测到。对这样的问题进行分层建模是很自然的，可观察的结果有条件地基于某些参数进行建模，这些参数本身就被赋予了进一步参数的概率规范，称为超参数。这种分层思维有助于理解多参数问题，也在开发计算策略方面发挥着重要作用。
也许在实践中更重要的是，简单的非分层模型通常不适合分层数据：参数很少，它们通常无法准确地拟合大型数据集，而参数很多，它们往往会“过度拟合”此类数据，因为它们生成的模型很好地拟合了现有数据，但会导致对新数据的预测较差。相比之下，层次模型可以有足够的参数来很好地拟合数据，同时使用总体分布来构建参数的一些相关性，从而避免过度拟合的问题。正如我们在本章的例子中所示，通常明智的做法是建立具有比数据点更多参数的分层模型。

在第5.1节中，我们考虑了使用分层原理构建先验分布的问题，但没有为分层结构建立正式的概率模型。我们首先考虑对单个实验的分析，使用历史数据创建先验分布，然后考虑一组实验参数的合理先验分布。第5.1节中的处理并不完全是贝叶斯的，因为为了说明的简单性，我们对种群分布的参数（超参数）使用点估计，而不是完全的联合后验分布。在第5.2节中，我们讨论了如何在完全贝叶斯分析的背景下构建分层先验分布。第5.3节至第5.4节通过结合分析方法和数值方法，介绍了共轭族中分层模型的一般计算方法。我们将最通用的计算方法的细节推迟到第三部分，以便立即探索分层贝叶斯模型的重要实用和概念优势。本章以两个扩展的例子继续：教育测试实验的分层模型和医学研究中使用的“元分析”方法的贝叶斯处理，以结合与同一研究问题相关的单独研究的结果。最后，我们讨论了弱信息先验，这对于适用于少数群体数据的层次模型来说变得很重要。

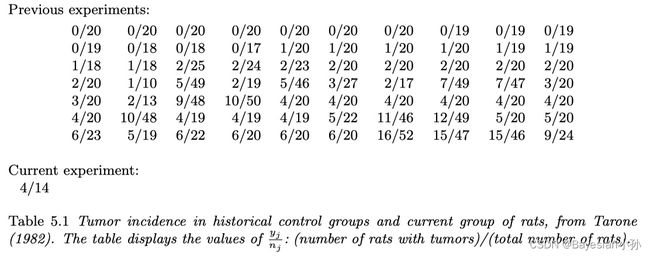
5.1 Constructing a parameterized prior distribution

5.1.1 Analyzing a single experiment in the context of historical data

为了开始我们对分层模型的描述，我们考虑了使用来自小型实验的数据和由类似的先前（或历史）实验构建的先验分布来估计参数$\theta$的问题。从数学上讲，我们将把当前和历史上的实验视为来自普通人群的随机样本。
在评估可能的临床应用药物时，通常对啮齿动物进行研究。对于从统计文献中得出的一项特定研究，假设直接目的是估计$\theta$，即接受零剂量药物的“F344”型雌性实验室大鼠群体（对照组）中发生肿瘤的概率。数据显示，14只大鼠中有4只患上了子宫内膜间质息肉（一种肿瘤）。在给定θ的情况下，很自然地假设肿瘤数量为二项式模型。为了方便起见，我们从共轭族中选择$\theta$的先验分布，$\theta \sim Beta(\alpha ,\beta )$。

Analysis with a fixed prior distribution. 根据历史数据，假设我们知道F344型雌性实验室大鼠组中的肿瘤概率$\theta$遵循近似的$Beta$分布，具有已知的平均值和标准差。由于大鼠体内的差异和实验之间的实验条件，肿瘤概率$\theta$会发生变化。参考$Beta$分布的平均值和方差的表达式（见附录A），我们可以确定$\alpha$、$\beta$的值，这些值对应于给定的均值和标准差值。然后，假设$\theta$的$Beta（\alpha ，\beta ）$先验分布产生$\theta$的后验分布$Beta（\alpha +4，\beta +10）$。
使用历史数据对人口分布的近似估计。 通常，潜在肿瘤风险的平均值和标准差是不可用的。相反，历史数据可以从以前对类似老鼠组的实验中获得。在大鼠肿瘤的例子中，历史数据实际上是70组大鼠肿瘤发生率的一组观察结果（表5.1）。在第$j$个历史实验中，假设患有肿瘤的大鼠数量为$y_j$，大鼠总数为$n_j$。我们将$y_j$建模为独立的二项式数据，给定样本量$n_j$和研究特定平均值${\theta }_j$。假设参数为$（\alpha ，\beta ）$的$Beta$先验分布很好地描述了历史实验中${\theta }_j$的种群分布，我们可以如图5.1所示示意性地显示分层模型，其中${\theta }_{71}$和$y_{71}$对应于当前实验。
观测到的70个样本的均值和标准差为0.136和0.103。
如果我们将总体分布的平均值和标准差设置为这些值，我们可以求解$\alpha$和$\beta$-见附录A第583页的（A.3）。$（\alpha ，\beta ）$的最终估计值为（1.4，8.6）。这不是贝叶斯计算，因为它不是基于任何特定的全概率模型。我们在第5.3节中提出了一种更好的、完全贝叶斯的方法来估计$(\alpha ,\beta )$。估计值$（1.4，8.6）$只是一个起点，我们可以从中探索估计人口分布参数的想法。
使用历史种群分布的简单估计作为当前实验的先验分布，得出${\theta }_{7}1$的$Beta（5.4，18.6）$的后验分布：后验平均值为0.223，标准差为0.083。先前的信息导致后验平均值显著低于粗略比例，4/14=0.286，因为经验的权重表明当前实验中的肿瘤数量异常高。
这些分析要求当前的肿瘤风险${\theta }_{71}$和70个历史肿瘤风险$\theta 1,...,{\theta }_{70}$，被认为是来自共同分布的随机样本，例如，如果已知历史实验都是在实验室a中进行的，但当前数据是在实验室B中收集的，或者如果时间趋势是相关的，则这一假设将无效。在实践中，一种简单但武断的解释当前数据和历史数据之间差异的方法是反映历史差异。对于贝塔模型，反映历史方差意味着在保持$\alpha /\beta$不变的同时减少$（\alpha +\beta ）$。其他系统差异，如肿瘤风险的时间趋势，可以纳入更广泛的模型中。
在使用70个历史实验形成${\theta }_{71}$的先验分布后，我们现在可能也希望使用相同的先验分布来获得前70个实验中肿瘤概率的贝叶斯推断,${\theta }_1,...,{\theta }_{70}$。根据现有数据直接估计先验分布的方法存在几个逻辑和实际问题：

1. 如果我们想使用估计的先验分布来推断前70个实验，那么数据将被使用两次：首先，所有结果一起用于估计先验分布，然后每个实验的结果用于估计其θ。这似乎会导致我们高估我们的精度。
2. $\alpha$和$\beta$的点估计似乎是任意的，对$\alpha$和$\beta$使用任何点估计都必然会忽略一些后验不确定性。
3. 我们也可以提出相反的观点：“估计”$\alpha$和$\beta$有意义吗？
   它们是“先验”分布的一部分：根据贝叶斯推理的逻辑，在收集数据之前是否应该知道它们？

5.1.2 组合信息的逻辑

尽管存在这些问题，但尝试从所有数据中估计人口分布，从而帮助估计每个${\theta }_j$，显然比单独估计所有71个值${\theta }_j$更有意义。考虑以下关于${\theta }_{26}$和${\theta }_{27}$这两个参数推断的思维实验，每个参数对应于对20只大鼠中的2个观察到的肿瘤进行的实验。假设${\theta }_{26}$和${\theta }_{27}$的先验分布都集中在0.15附近；现在假设你在完成数据分析后被告知${\theta }_{26}=0.1$。这应该会影响您对${\theta }_{27}$的估计；事实上，这可能会让你认为${\theta }_{27}$比你之前认为的要低，因为这两个参数的数据是相同的，而且0.1的假设值比你之前从先验分布中预期的${\theta }_{26}$要低。因此，${\theta }_{26}$和${\theta }_{27}$在后验分布中应该是依赖的，不应该单独分析。

我们保留了使用数据来估计先前参数的优点，并通过对整个参数和实验集建立概率模型，然后对所有模型参数的联合分布进行贝叶斯分析，消除了刚才提到的所有缺点。完整的贝叶斯分析如第5.3节所述。使用数据来估计先验参数的分析，有时被称为经验贝叶斯（$empiricalBayes$），可以被视为对完整的分层贝叶斯分析的近似。我们倾向于避免使用“经验贝叶斯”一词，因为它误导性地表明，我们在这里讨论并在本书其余部分使用的完整贝叶斯方法不是“经验的”。

5.2 可交换性和建立分层模型

从上一节的例子中概括，考虑一组实验$j=1,...,J$、 其中实验$J$具有数据（向量）$y_j$和参数（向量）${\theta }_J$，似然性为$p(y_j|{\theta }_J)$。
（在本章中，为了方便起见，我们使用了“实验”一词，但这些方法同样适用于非实验数据。）不同实验中的一些参数可能重叠；例如，每个数据向量$y_j$可以是具有平均值${\mu }_j$和共同方差${\sigma }^2$的正态分布的观测样本，在这种情况下${\theta }_j=({\mu }_j，{\sigma }^2)$。为了创建所有参数$\theta$的联合概率模型，我们使用了第一章中引入的可交换性的关键思想，并从那时起重复使用。

5.2.1 可交换性质$Exchangeability$

如果除了数据$y$之外没有其他信息可用于区分任何${\theta }_j$和其他${\theta }_j$，并且不能对参数进行排序或分组，则必须假设参数在其先前分布中的对称性。这种对称性可以用可交换性来表示；如果$p({\theta }_1，\dots ，{\theta }_J）$对参数$({\theta }_1,...,{\theta }_J）$的排列是不变的，则参数$({\theta }_1,...,{\theta }_J）$在其联合分布中是可交换的。例如，在大鼠肿瘤问题中，假设我们没有信息来区分71个实验，除了样本量$n_j$，这可能与${\theta }_j$的值无关；因此，我们使用${\theta }_j$的可交换模型。

在为直接数据构建独立且同分布的模型时，我们已经遇到了可交换性的概念。在实践中，$ignorance$意味着可交换性。一般来说，我们对一个问题了解得越少，就越能自信地宣称其可交换性。（我们赶紧补充说，这并不是在开始统计分析之前限制我们对问题的了解的好理由，这可能会使我们倾向于一种结果而不是其他结果，从而消除六种结果之间的对称性。
可交换分布的最简单形式是，每个参数${\theta }_j$都是由一些未知参数向量$\varphi$控制的先验（或总体）分布的独立样本；因此:
$$p(\theta |\varphi )=\prod _{j=1}^{J}p({\theta }_j|\varphi )$$
一般来说，$\varphi$是未知的，所以我们对θ的分布必须在$\varphi$中的不确定性上取平均值：
$$p(\theta )={\int }_{\varphi }(\prod _{j=1}^{J}p({\theta }_j|\varphi ))p(\varphi )d\varphi$$
这种形式，独立的相同分布的混合，通常是我们在实践中捕捉可交换性所需要的全部。
作为上述混合模型的一个简单反例，考虑给定模具落在其六个面上的概率。概率${\theta }_1,...,{\theta }_6$是可交换的，但六个参数${\theta }_j$被约束为和为1，因此不能用独立的相同分布的混合建模；尽管如此，它们可以互换的建模。

可交换性和采样的实例

下面的思维实验说明了可交换性在随机抽样推理中的作用。为了简单起见，我们使用了一个在$y$而不是$\theta$级别上具有可交换性的非分层示例。

我们从美国选出了八个州，并记录了1981年每个州每1000人的离婚率。将这些称为$y_1,...,y_8$。你对第八州的离婚率$y_8$有什么看法？
由于您没有信息将这八个州中的任何一个州与其他州区分开来，因此您必须以可交换的方式对它们进行建模。您可以使用八个$y_j$的$Beta$分布、$logit$正态分布或其他限制在[0，1]范围内的先验分布。除非你熟悉美国的离婚统计数据，否则你在$y_1,...,y_8$上的分布应该相当模糊。

我们现在从这八个州中随机抽取七个州，告诉你他们的离婚率：5.8、6.6、7.8、5.6、7.0、7.1、5.4，每个州每1000人（每年）的离婚率。主要基于数据，剩余值$y_8$的合理后验（预测）分布可能集中在6.5左右，其大部分质量在5.0到8.0之间。**更改索引不会更改关节分布。**如果我们将剩余值重新标记为任何其他$y_j$，则后验估计将是相同的。$y_j$是可交换的，但它们不是独立的，因为我们假设第八个未观测状态下的离婚率可能与观测到的离婚率相似。

假设最初我们给了你进一步的事先信息，这八个州是山区州：亚利桑那州、科罗拉多州、爱达荷州、蒙大拿州、内华达州、新墨西哥州、犹他州和怀俄明州，但是随机选择的；你仍然没有被告知哪个观察到的速率对应于哪个状态。现在，在观察这七个数据点之前，这八个离婚率仍然应该是可交换的模型。然而，你之前的分布（也就是说，在看到数据之前），对于这八个数字应该会改变：可以合理地假设，拥有大量摩门教人口的犹他州的离婚率要低得多，而拥有自由离婚法的内华达州的离婚率要比其他六个州高得多。也许，考虑到您对分布中异常值的预期，您之前的分布应该有很宽的尾部。考虑到这些额外的信息（八个州的名称），当你看到七个观测值，并注意到这些数字非常接近时，可能会合理地猜测缺失的第八个州是内华达州或犹他州。因此，它的值可能比观察到的七个值低得多或高得多。这可能导致双峰或三峰后验分布，以解释这两种可能的情况。然而，八个值$y_j$上的先验分布仍然是可交换的，因为您没有信息告诉哪个状态对应于哪个索引号。（请参阅练习5.6。）
最后，我们告诉您，未采样的州（对应于$y_8$）是内华达州。现在，即使在看到七个观测值之前，你也无法将可交换的先验分布分配给八个离婚率的集合，因为你有信息将$y_8$与其他七个数字区分开来，这里怀疑它比其他任何数字都大。$y_1,...,y_7$已经被观测到，$y_8$的合理后验分布似乎应该使其大部分质量高于最大观测速率，即，$p(y_8>max(y_1,...,y_7)|y_1,...,y_7)$应该很大。顺便说一句，内华达州1981年的离婚率为每1000人有13.9人。

单元上有额外信息时的可交换性

观测结果通常不是完全可交换的，而是部分或有条件可交换的：

• 如果观察结果可以分组，我们可以建立层次模型，其中每个组都有自己的子模型，但组的特征未知。如果我们假设组的特征是可交换的，我们可以对组的特征使用一个通用的先验分布。
• 如果$y_i$有额外的信息$x_i$，使得$y_i$不可交换，但$(y_i,x_i)$仍然可交换，那么我们可以为$(y_i,x_i)$建立一个联合模型或条件概率$y_i|x_i$。

在大鼠肿瘤的例子中，$y_j$是可交换的，因为没有关于实验条件的额外知识。如果我们知道特定批次的实验是在不同的实验室中进行的，我们可以假设部分可交换性，并使用两级层次模型来模拟每个实验室内和实验室之间的变化。

在离婚的例子中，如果我们知道$x_j$，即去年$j$州的离婚率，对于$j=1,...,8$，但不是哪个索引对应于哪个状态，那么我们肯定能够区分$y_j$的八个值，但联合先验分布$p(x_j,y_j)$对于每个状态都是相同的。对于具有相同去年离婚率$x_j$的州，我们可以使用分组并假设部分可交换性，或者如果$x_j$有许多可能的值（正如我们对离婚率的假设），我们可以假设条件可交换性并在回归模型中使用$x_j$作为协变量。

一般来说，用协变量对可交换性进行建模的通常方法是通过条件独立性：
$$p({\theta }_1,...,{\theta }_J|x_1,...{,}_J)=\int [\prod _{j=1}^{J}p({\theta }_j|\varphi ,x_j)]p(\varphi |x)d\varphi$$
$$x=(x_1,...,x_J)$$
通过这种方式，可交换模型变得几乎普遍适用，因为任何可用于区分不同单位的信息都应该编码在x和y变量中。

对可交换模型的反对意见

在几乎任何统计应用中，都很自然地会以单位实际不同为由反对可交换性。例如，71个大鼠肿瘤实验在不同的时间、不同的大鼠身上进行，可能在不同的实验室进行。然而，这些信息并不会使可交换性失效。实验的差异意味着{θ_j}的差异，但将其视为来自共同分布可能是完全可以接受的。事实上，由于没有可用的信息来区分它们，我们别无选择，只能以可交换的方式对{θ_j}进行建模。对无知建模的可交换性的反对并不比对来自普通群体的样本的独立和同分布模型的反对、对一般回归模型的反对，或者就这一点而言，反对在没有单独标签的散点图中显示点更合理。与回归一样，有效的关注点不是可交换性，而是尽可能将相关知识编码为解释变量。

5.3分层模型的完全贝叶斯处理

回到推理问题，这些模型的关键“层次”部分是$\varphi$是未知的，因此有自己的先验分布$p(\varphi )$。适当的贝叶斯后验分布是向量$(\varphi ,\theta )$。联合先验分布是：
$$p(\varphi ,\theta )=p(\varphi )p(\theta |\varphi )$$
and the joint posterior distribution is：
$$p(\varphi ,\theta |y)\propto p(\varphi ,\theta )p(y|\varphi ,\theta )=p(\varphi ,\theta )p(y|\theta )$$
后一种简化成立，因为数据分布$p(y|\varphi ,\theta )$仅取决于$\theta$；超参数$\varphi$仅通过$\theta$影响$y$。以前，我们假设$\varphi$是已知的，这是不现实的；现在我们将$\varphi$中的不确定性包括在模型中。

The hyperprior distribution

为了创建$(\varphi ,\theta )$的联合概率分布，我们必须为$\varphi$分配先验分布。如果对$\varphi$知之甚少，我们可以指定不同的先验分布，但当使用不适当的先验密度来检查结果的后验分布是否正确时，我们必须小心，并且我们应该评估我们的结论是否对这种简化假设敏感。在大多数实际问题中，如果不分配实质性的超先验分布，则至少应该对$\varphi$中的参数有足够的实质性知识，以将超参数约束在有限区域内。与非层次模型一样，通常从$\varphi$上的简单、相对非形成性的先验分布开始，如果后验分布仍有太多变化，则寻求添加更多的先验信息。
在大鼠肿瘤的例子中，超参数是$(\alpha ,\beta )$，它决定了$\theta$的$Beta$分布。我们在下一节的例子的延续中说明了一种构建适当超优先分布的方法。

后验预测分布
分层模型的特征既有超参数$\varphi$（在我们的符号中），也有参数$\theta$。有两种后验预测分布可能会引起数据分析师的兴趣：（1）与现有${\theta }_j$相对应的未来观测值$y$的分布，或（2）与未来$\theta$对应的观测值θ的分布来自同一超群体。我们将未来θj标记为。正如我们在第6章中所讨论的，这两种复制都可以用于评估模型的充分性。在大鼠肿瘤的例子中，未来的观察可以是（1）来自现有实验的额外大鼠，或者（2）来自未来实验的结果。在前一种情况下，后验预测图_{y是基于现有实验的θj的}θ后验图。在后一种情况下，在给定φ的后验图的情况下，必须首先从_{θ总体分布中绘制新实验，然后在给定模拟的情况下绘制}y。