代码随想录_二叉树_leetcode 701 450
leetcode701. 二叉搜索树中的插入操作
701. 二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
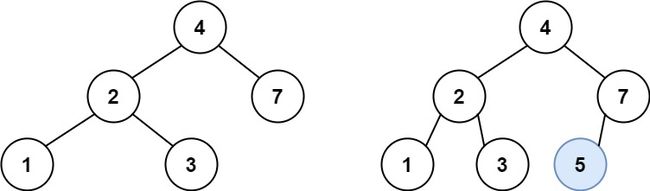
示例 1:
输入:root = [4,2,7,1,3], val = 5 输出:[4,2,7,1,3,5] 解释:另一个满足题目要求可以通过的树是:示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25 输出:[40,20,60,10,30,50,70,null,null,25]示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5 输出:[4,2,7,1,3,5]
代码
// leetcode701. 二叉搜索树中的插入操作
// 迭代递归都可,这里选择递归
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (root == nullptr)
{
TreeNode* cur = new TreeNode(val);
return cur;
}
if (root->val > val)
{
root->left = insertIntoBST(root->left, val);
}
else if (root->val < val)
{
root->right = insertIntoBST(root->right, val);
}
return root;
}
};leetcode450. 删除二叉搜索树中的节点
450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:
输入:root = [5,3,6,2,4,null,7], key = 3 输出:[5,4,6,2,null,null,7] 解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。 一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。 另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0 输出: [5,3,6,2,4,null,7] 解释: 二叉树不包含值为 0 的节点示例 3:
输入: root = [], key = 0 输出: []
代码
// leetcode450. 删除二叉搜索树中的节点
// 删除和插入节点不同,删除还要考虑删除结点的左子树和右子树
class Solution {
public:
TreeNode* deleteOneNode(TreeNode* target)
{
if (target->left == nullptr && target->right == nullptr)
{
//左右孩子都为空
return nullptr;
}
else if (target->left == nullptr && target->right != nullptr)
{
// 左孩子为空 右孩子不为空
return target->right;
}
else if (target->left != nullptr && target->right == nullptr)
{
// 左孩子不为空 右孩子为空
return target->left;
}
else
{
TreeNode* cur = target->right;
while (cur->left != nullptr)
{
cur = cur->left;
}
// 左右孩子都不为空
cur->left = target->left;
}
return target->right;
}
TreeNode* deleteNode(TreeNode* root, int key) {
TreeNode* pre = nullptr;
TreeNode* cur = root;
bool flag = false; //判断是否找到删除结点
while (cur != nullptr)
{
if (cur->val == key)
{
flag = true;
break;
}
else if (cur->val > key)
{
pre = cur;
cur = cur->left;
}
else
{
pre = cur;
cur = cur->right;
}
}
if (flag)
{
if (pre == nullptr)
{
// 删除的是根节点
return deleteOneNode(cur);
}
else if (pre->left != nullptr && pre->left->val == key)
{
//删除的是pre的左结点
pre->left = deleteOneNode(cur);
}
else if (pre->right != nullptr && pre->right->val == key)
{
//删除的是pre的右结点
pre->right = deleteOneNode(cur);
}
}
return root;
}
};