时间序列数据的白噪声检验
问题起源
只有数据平稳,才可以借数据。
只有借数据,才可以做分析。
什么是白噪声序列
白噪声序列也称为纯随机序列,它满足两个性质
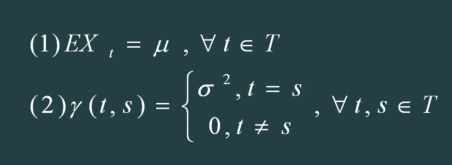
1)数据是平稳的
2)t≠s的时候,方差为0,说明t和s没有线性的关系
白噪声的性质
在白噪声的图上,我们无法抓到规律,因此,我们把握以下性质:
各序列值之间没有任何的相关关系,即为“没有记忆”的白噪声序列
2)方差齐性
方差等于一个常数。
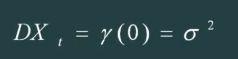
根据Markov定理,只有方差齐性假设成立时,用最小二乘法得到的未知参数估计值才是最准确有效的。
(数据平稳一定同方差)
跨越1步,2步,3步…是不是相关系数为0呢?
如果一个序列是纯随机的,得到一个观察期数为n的观察序列,那么该序列的延迟非零期的样本自相关系数将近似服从均值为0,方差序列观察期数倒数的正态分布。
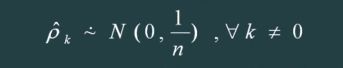
原假设:延迟期数小于或等于m期的序列值之间相互独立
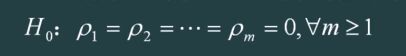
备择假设:延迟期数小于或等于k期的序列值之间有相关性
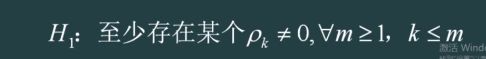
平稳数据一般有短期相关性,延迟系数较大的一定为0,一般跨越6步、12步、18步。这三个都为0的话,别的就不需要检验了。
检验原假设的时候,有两个检验,用得最多的是LB检验。
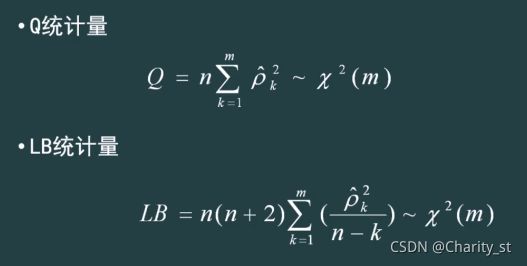

如果有相关性,则可以建立一定的函数关系进行预测。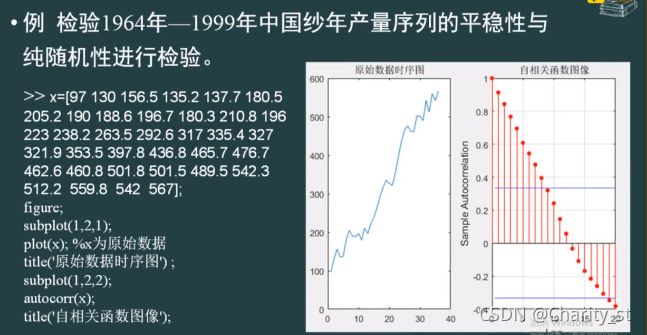
x=[97 130 156.5 135.2 137.7 180.5 205.2 190 188.6 196.7 180.3 210.8 196 223 238.2 263.5 292.6 317 335.4 327 321.9 353.5 397.8 436.8 465.7 476.7 462.6 460.8 501.8 501.5 489.5 542.3 512.2 559.8 542 567];
figure;
subplot(1,2,1);%画一行两列第一个图
plot(x)
title('原始数据时序图');
subplot(1,2,2);%画一行两列第二个图
autocorr(x);
title('自相关函数图像');
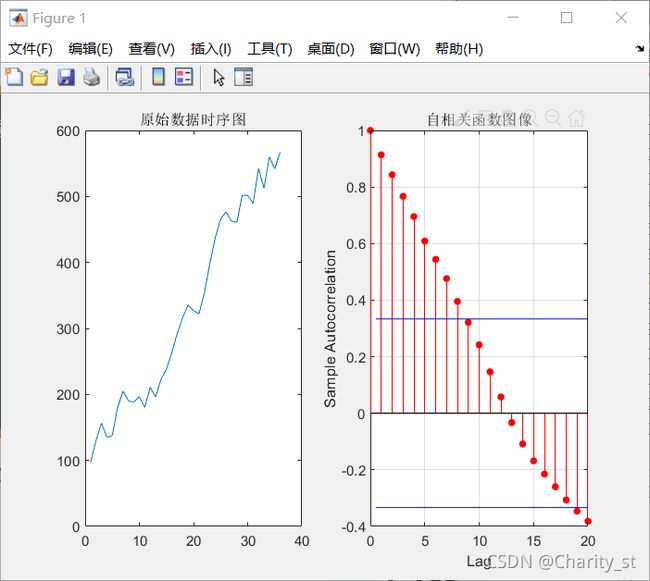
显然,这不是无关的,表现一阶差分之后的数据平稳性。
非平稳的转化为平稳的,向下向上趋势,差分一次。周期性则多少步的差分。
x=[97 130 156.5 135.2 137.7 180.5 205.2 190 188.6 196.7 180.3 210.8 196 223 238.2 263.5 292.6 317 335.4 327 321.9 353.5 397.8 436.8 465.7 476.7 462.6 460.8 501.8 501.5 489.5 542.3 512.2 559.8 542 567];
figure;
subplot(1,2,1);%画一行两列第一个图
plot(x)
title('原始数据时序图');
subplot(1,2,2);%画一行两列第二个图
autocorr(x);
title('自相关函数图像');
x=x';
x1=diff(x);%求差分,把不是平稳的数据变成平稳的
[h1,p1,adf,ljz]=adftest(x1)
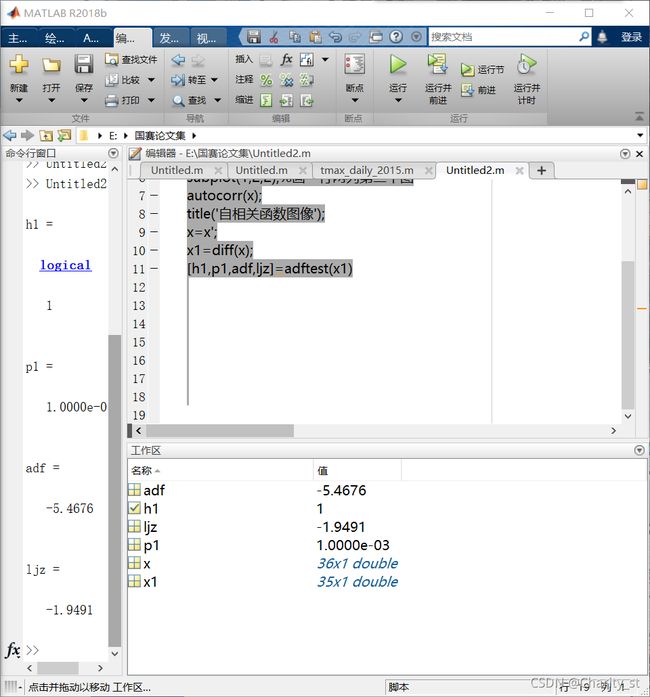
不平稳数据,差分后可以看出是平稳的。自相关图出现了短期相关性。
不平稳数据变成平稳的,就可以做了。
N阶差分:消除向上向下趋势的
N步差分:消除周期性的
x=[97 130 156.5 135.2 137.7 180.5 205.2 190 188.6 196.7 180.3 210.8 196 223 238.2 263.5 292.6 317 335.4 327 321.9 353.5 397.8 436.8 465.7 476.7 462.6 460.8 501.8 501.5 489.5 542.3 512.2 559.8 542 567];
figure;
subplot(1,2,1);%画一行两列第一个图
plot(x)
title('原始数据时序图');
subplot(1,2,2);%画一行两列第二个图
autocorr(x);
title('自相关函数图像');
x=x';
x1=diff(x);
[h1,p1,adf,ljz]=adftest(x1)
%白噪声检验,继续用前面的一阶差分之后的数据x1
yanchi=[6,12,18];
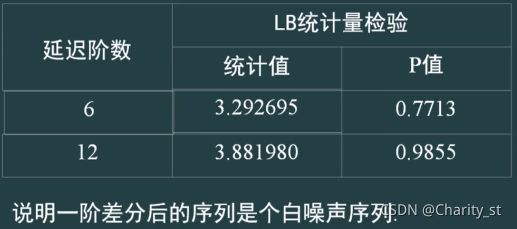
[H,pValue,Qstat,CriticalValue]=lbqtest(x1,'lags',yanchi);
%按照统计表格形式,打印相应的统计量
fprintf('%15s%15s%15s','延迟阶数','卡方统计量','p值');
fprintf('\n');
for i=1:length(yanchi)
fprintf('%18f%19f%19f',yanchi(i),Qstat(i),pValue(i));
fprintf('\n');
end

H-判断的结果
pValue-概率
Qstat-统计量
CriticalValue-临界值
x1-数据
‘lags’-按照步长
yanchi-延迟
%15s-后面的几个字在界面哪一个位置,空出几个位置
length–提取长度