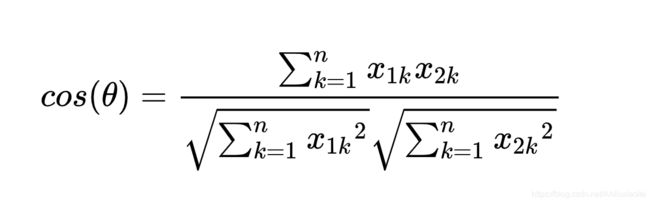
余弦相似度计算

0：从矩阵到tensor

tensor可以理解为一个多维矩阵。




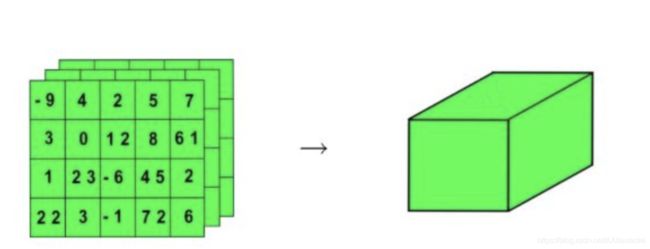
一个二维张量，就是一个一维数组里面的所有元素都是一个一维张量；
一个三维张量，就是一个一维数组里面的所有元素都是一个二维张量；
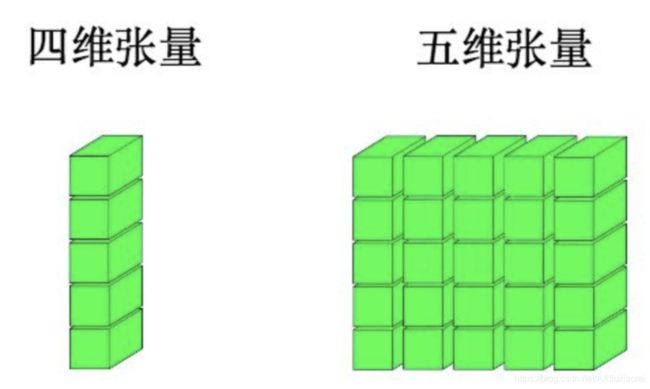
一个四维张量，就是一个一维数组里面的所有元素都是一个三维张量；

用Pytorch可以很清楚的看到：

.. x1 = torch.Tensor(2)
... x2 = torch.Tensor(2,2)
... x3 = torch.Tensor(2,2,2)
... x4 = torch.Tensor(2,2,2,2)
... print(x1,'\n')
... print(x2,'\n')
... print(x3,'\n')
... print(x4,'\n')

... 
tensor([4.3790e-36, 0.0000e+00]) 

tensor([[0.0000e+00, 0.0000e+00],
        [4.5340e-36, 0.0000e+00]]) 
        
tensor([[[1.4013e-45, 0.0000e+00],
         [2.8026e-45, 0.0000e+00]],

        [[0.0000e+00, 0.0000e+00],
         [0.0000e+00, 0.0000e+00]]]) 
         
tensor([[[[0.0000e+00, 0.0000e+00],
          [0.0000e+00, 0.0000e+00]],
         [[4.5253e-36, 0.0000e+00],
          [0.0000e+00, 0.0000e+00]]],
          
        [[[4.2039e-45, 0.0000e+00],
          [1.4013e-45, 0.0000e+00]],
         [[1.4013e-45, 0.0000e+00],
          [1.4013e-45, 0.0000e+00]]]]) 

1: 什么是余弦相似度

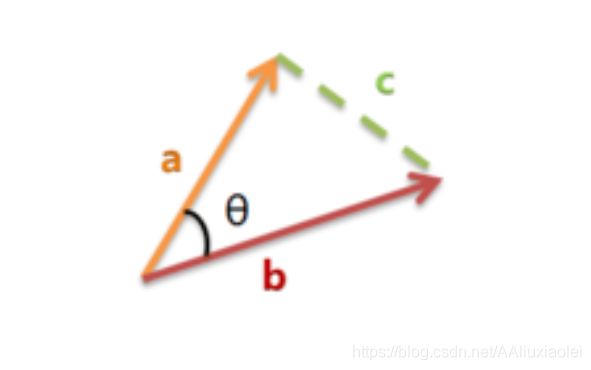
余弦相似度可以理解为：a 投影在b上，重合越多那么相似度越大。在三角函数中，要想|a| * |b| * con ab之间的夹角 的积越大，则需要夹角余弦趋近于1，也就是角大小趋近0度，即两个向量越近似。

2：代码实现

公式如图

x = torch.tensor([1.0,1.0])
y = torch.tensor([1.0,2.0])
c = torch.cosine_similarity(x,y,dim = 0 )
print(c)

3：参考资料

tensor：
https://zhuanlan.zhihu.com/p/339551567
https://zhuanlan.zhihu.com/p/48982978

余弦相似度：
https://zhuanlan.zhihu.com/p/33164335