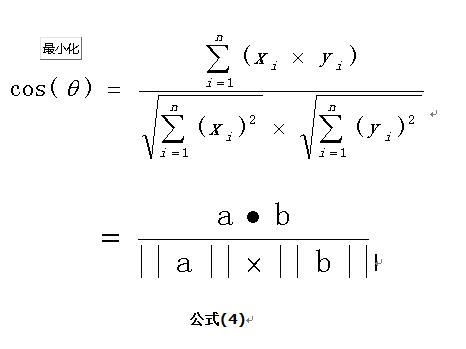词句相似度计算——余弦相似度

余弦相似度，是一种通过判断两个向量的夹角来判断其相似性的数学方法。

举个栗子：

A:中国工商银行北京分部北京支行

B:中国招商银行广西分部桂林支行

我们用“余弦相似度”的办法来判断这两个句子的相似性

1、分词！

第一步要做的肯定是分词，把一个句子分成一组一组的散词，分词一般我们会用现成的语料库，比如结巴分词是吧，传说中的最好用的中文分词模块包。如果不是专业性特别强的方向，足矣，如果是专项的，比如医学、金融学、药学等专业相关，那肯定得自己构建一套自己的分词系统，不过这些网上也是一堆一堆的。怎么分词，待会咱们代码见！

2、词转向量

假设我们已经分好了词：

A:中国、工商银行、北京、分部、北京、支行

B:中国、招商银行、广西、分部、桂林、支行

这样我们就有了一个局部语料库，bags=['中国', '工商银行', '招商银行', '北京', '广西','支行','桂林', '分部']，这是个有序集合（最好是有序）

                     ['中国', '工商银行', '招商银行', '北京', '广西','支行','桂林', '分部']

对于A而言，                     

向量为：      [1               1                  0                2           0       1         0           1]

对于B而言，

向量为：      [1               0                  1                0           1        1         1           1]

其中，每一个数字表示：局部语料库中的词在A（或B）中出现的次数 

于是，通过这种方法，词就转成了向量

 

3、计算余弦相似度

首相，余弦相似度是这么定义的：

（引自：https://www.cnblogs.com/dsgcBlogs/p/8619566.html）

举个栗子，a = [1,2,3], b=[5,6,7]

a和b的余弦相似度就是

                                           

于是我们得出“中国工商银行北京分部北京支行”和“中国招商银行广西分部桂林支行”的相似度为

                 

这个值越接近1，相似度越高

 

那么！这有啥问题！

假设，我们把“桂林”，改成“南宁”，得出来的余弦相似度是一样的！！！

但是，实际上，桂林支行和南宁支行是不一样的，我们用不一样的词得出了一样的结果！！！

那怎么办？

于是乎，人们想出了一个算法，叫TF-IDF

之前我们所有的计算，全部基于当前的“局部语料库”，TF-IDF算法基于更大语料库，暂且命名为“整体语料库”吧。那既然不同的词有不同的结果，我们就给不同的词加一个系数吧，这个系数怎么来？

（引自：https://www.cnblogs.com/pinard/p/6693230.html）

这个系数等于

                                                                                       

其中N表示总词数，n表示包含某个词（比如桂林、南宁、苹果等）的总词数，举个栗子：

咱们整体语料库一共有1024个词，而包含桂林两个字的有256个词，而包含南宁两个字的只有16个词，

则,                   

在假设除开桂林和南宁的系数都是1的前提下：

A         =  [1               1                  0                2           0       1         0           1]

B桂林 =  [1               0                  1                0           1        1         1*2        1]

B南宁 =  [1               0                  1                0           1        1         1*6        1]

注意：只是假设其他的词的系数为1，但是实际上不可能，这里只是为了方便说明

IDF系数越大，说明n越小，n越小说明使用的次数使用的地方越少；

同时，因为IDF系数越大，跟A的余弦值越小（夹角越大），那么相似度就越小

也就是说：用得越频繁的词，可能跟某个句子的相似度就越大；用得越不频繁的词，相似度就可能越小。

这样，就把一个词的使用频率也加进来了。结巴分词，就做了这一点。在结巴分词里，桂林的IDF要小于南宁的IDF，也就是说：在某一程度上，桂林和北京的关联性要比南宁跟北京的关联性要强一些

 

于是乎，余弦相似度进一步升级为加入了相关系数的乘法计算。以下附python代码

import numpy as np
import jieba
import jieba.analyse
from collections import Counter

def word_2_vec(words1, words2):
    # 词向量
    words1_info = jieba.analyse.extract_tags(words1, withWeight=True)
    words2_info = jieba.analyse.extract_tags(words2, withWeight=True)
    # 转成counter不需要考虑0的情况
    words1_dict = Counter({i[0]: i[1] for i in words1_info})
    words2_dict = Counter({i[0]: i[1] for i in words2_info})
    bags = set(words1_dict.keys()).union(set(words2_dict.keys()))
    # 转成list对debug比较方便吗，防止循环集合每次结果不一致
    bags = sorted(list(bags))
    vec_words1 = [words1_dict[i] for i in bags]
    vec_words2 = [words2_dict[i] for i in bags]
    # 转numpy
    vec_words1 = np.asarray(vec_words1, dtype=np.float)
    vec_words2 = np.asarray(vec_words2, dtype=np.float)
    return vec_words1, vec_words2


def cosine_similarity(v1, v2):
    # 余弦相似度
    v1, v2 = np.asarray(v1, dtype=np.float), np.asarray(v2, dtype=np.float)
    up = np.dot(v1, v2)
    down = np.linalg.norm(v1) * np.linalg.norm(v2)
    return round(up / down, 3)

cosine_similarity(*word_2_vec('中国工商银行北京分部北京支行', '中国招商银行广西分部南宁支行'
))