PLS-DA分类的实现(基于sklearn)

目录

简单介绍

代码实现

数据集划分

选择因子个数

模型训练并分类

调用函数

---

简单介绍

（此处取自各处资料）    

    PLS-DA既可以用来分类，也可以用来降维，与PCA不同的是，PCA是无监督的，PLS-DA是有监督的。与PCA不同，PCA是无监督,PLS是“有监督”模式的偏最小二乘法分析，当样本组间差异大而组内差异小时，无监督分析方法可以很好的区分组间差异。反之样本组间差异不大，无监督的方法就难以区分组间差异。另外如果组间的差异较小，各组的样本量相差较大，样本量大的那组将会主导模型。有监督的分析（PLS-DA）能够很好的解决这些问题。也就是在分析数据时，已知样本的分组关系，这样可以更好的选择区分各组的特征变量，确定样本之间的关系。DA是判别分析，PLS-DA用偏最小二乘回归的方法，在对数据“降维”的同时，建立了回归模型，并对回归结果进行判别分析。

    本文主要是基于PLS的分类展开。

代码实现

主要参考了这位大佬的: https://zhuanlan.zhihu.com/p/374412915

数据集划分

    首先要把数据集处理成一定的格式，也就是把自变量和因变量搞清楚，做好数据集的分割，然后传回。

def deal_data(path):
    # 读取自变量和因变量构成的数据矩阵,类别y放最后一列,前面均为x
    spec = pd.read_excel(path)
    spec = np.array(spec)  # 直接转化为numpy类型
    x = spec[:, 0:-1]  # 前面的列均为自变量
    y = spec[:,-1]

    # 先做一个数据集的划分
    train_X, test_X, train_y, test_y = train_test_split(x, y, test_size=0.2)
    return train_X, test_X, train_y, test_y

选择因子个数

    PLS类似于PCA，是有成分这么一个说法的，不同的成分个数最终得到的效果也不一样，因此我们对于不同的成分个数均进行训练，然后进行交叉验证，观察不同成分个数的表现，从而选择合适的个数。

def accuracy_component(xc, xv, yc, yv, component=8, n_fold=5):
    # xc表示训练集,xv表示测试集,yc表示训练标签,yv表示测试标签,component表示最多个数,n_fold表示分为几组样本(每次一组作为测试集,交叉验证)
    k_range = np.linspace(start=1, stop=component, num=component)

    kf = KFold(n_splits=n_fold, random_state=None, shuffle=True)  # n_splits表示要分割为多少个K子集,交叉验证需要

    accuracy_validation = np.zeros((1, component))  # 用于存储各个成分数的测试平均精准度accuracy
    accuracy_train = np.zeros((1, component))  # 用于存储各个成分数的训练平均精准度accuracy
    for j in range(component):  # j∈[0,component-1],j+1∈[1,component]
        p = 0
        acc = 0  # acc表示总的精准度,p表示个数,acc/p平均精确度
        # 下面是普通训练
        model_pls = PLSRegression(n_components=j + 1)  # 此时选择component个成分
        yc_labels = pd.get_dummies(yc)
        model_pls.fit(xc, yc_labels)
        y_pred = model_pls.predict(xv)
        y_pred = np.array([np.argmax(i) for i in y_pred])
        accuracy_train[:, j] = accuracy_score(yv, y_pred)  # 这是直接训练的
        # 下面是交叉验证
        for train_index, test_index in kf.split(xc):  # 进行n_fold轮交叉验证
            # 划分数据集
            X_train, X_test = xc[train_index], xc[test_index]
            y_train, y_test = yc[train_index], yc[test_index]
            YC_labels = pd.get_dummies(y_train)  # 训练数据结果独热编码
            model_1 = PLSRegression(n_components=j + 1)
            model_1.fit(X_train, YC_labels)
            Y_pred = model_1.predict(X_test)
            Y_pred = np.array([np.argmax(i1) for i1 in Y_pred])  # 独热编码转化成类别变量
            acc = accuracy_score(y_test, Y_pred) + acc
            p = p + 1
        accuracy_validation[:, j] = acc / p  # 计算j+1个成分的平均精准度
    # 首先对于每个component数训练一个模型,然后利用测试集得出准确率
    print('模型训练的准确率')
    print(accuracy_train)
    # 然后对样本的训练集进行交叉验证
    print('交叉验证的平均准确率')
    print(accuracy_validation)
    plt.plot(k_range, accuracy_train.T, 'o-', label="Training", color="r")
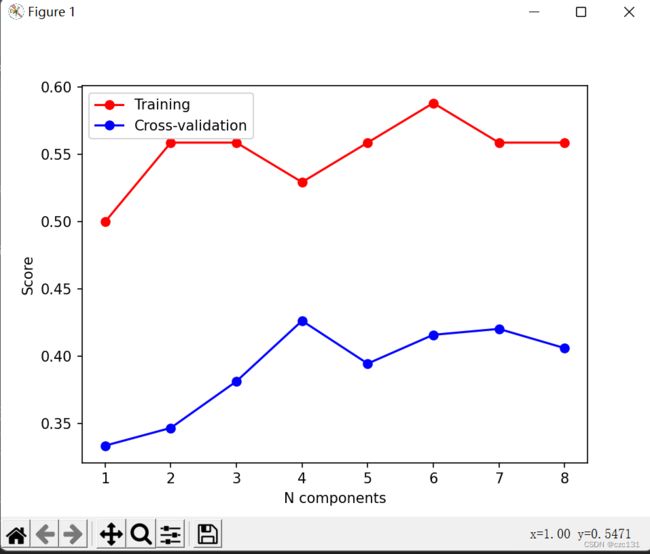
    plt.plot(k_range, accuracy_validation.T, 'o-', label="Cross-validation", color="b")
    plt.xlabel("N components")
    plt.ylabel("Score")
    plt.legend(loc="best")  # 选取最佳位置标注图注
    plt.rc('font', family='Times New Roman')
    plt.rcParams['font.size'] = 10
    plt.show()
    return accuracy_validation, accuracy_train

    下面是运行效果，因为数据是乱造的所以参数就不用关注了，这样来看的话三到四个因子效果还不错。

模型训练并分类

    下面就是选择合适的成分个数进行分类，得到混淆矩阵和一些参数指标。

def PLS_DA(train_X, test_X, train_y, test_y):
    # 建模
    model = PLSRegression(n_components=6)
    train_y = pd.get_dummies(train_y)
    model.fit(train_X, train_y)
    # 预测
    y_pred = model.predict(test_X)
    # 将预测结果（类别矩阵）转换为数值标签
    y_pred = np.array([np.argmax(i) for i in y_pred])
    # 模型评价---混淆矩阵和精度
    print('测试集混淆矩阵为：\n', confusion_matrix(test_y, y_pred))
    print('平均分类准确率为：\n', accuracy_score(test_y, y_pred))

     运行效果，至少比乱分类的33%正确率要高。

调用函数

     以上都是各个组件，最后需要一个主函数调用串联起来，如下，    建议分步调用，也便于问题的发现和处理。

max_component = 8 # 迭代最大成分数
n_fold = 10  # 交叉验证次数
excel_path = './data.xlsx'  # 数据集地址
if __name__ == '__main__':
    train_X, test_X, train_y, test_y = deal_data(excel_path)  # 处理数据,返回处理完的训练和测试集,具体情况具体分析
    # accuracy_component(train_X, test_X, train_y, test_y, max_component, n_fold)
    PLS_DA(train_X, test_X, train_y, test_y,n_components=3)