BZOJ3153 : Sone1
Top Tree模板题,写起来真不是一般的蛋疼,调了两天。常数写渣了TAT
Top Tree就是在LCT的基础上加以改动,将虚边也用splay维护,

对于A向儿子所连出去的虚边,用Splay维护↓

为了保证所有虚儿子不存在父子关系,需要让它们都是叶子节点,所以需要引入白色的内部点来维持这个结构。
就能支持子树操作了。

对于这样一棵以1为根的树。
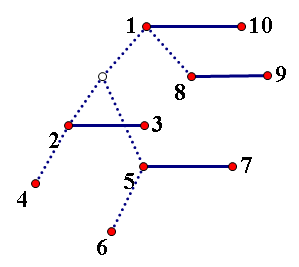
在Top Tree中是这样维护的。
实现起来就是把原来son[2]扩充到son[4]
son[0]和son[1]仍然对应实链splay的两个儿子
son[2]和son[3]对应虚边splay的两个儿子
Add操作:
Add(x,y)操作就是从x点连一条虚边到y,使得x是y的父亲。
这就等价于在x的虚边splay中插入y这个叶子节点,必要的话要新建内部点。
Del操作:
Del(x)操作就是把x点和它父亲之间连着的虚边断开。
这就等价于在x的父亲的虚边splay中删除x这个叶子节点,必要的话要删除某些已经没用的内部点。
Access操作:
Access(x)操作就是把x到根路径上的所有边都变成实边,并把x向它所有儿子的边都变成虚边。
考虑普通Link-Cut Tree的Access过程:
void access(int x){
for(int y=0;x;y=x,x=f[x]){
splay(x);
son[x][1]=y;
up(x);
}
}
每一步都是实边虚边的转化,有了Add和Del操作,可以很自然的改写成:
void access(int x){
for(int y=0;x;y=x,x=fa(x)){
splay(x);
del(y);
add(x,son[x][1]);
setson(x,1,y);
up(x);
}
}
Makeroot操作:
与Link-Cut Tree一致,注意翻转只交换son[0]和son[1]。
Link操作:
考虑普通Link-Cut Tree的Link过程:
void link(int x,int y){
makeroot(x);
f[x]=y;
access(x);
}
可以很自然的改写成:
void link(int x,int y){
makeroot(x);
add(y,x);
access(x);
}
Cut操作:
与Link-Cut Tree一致。
链操作:
与Link-Cut Tree一致。
子树操作:
方便起见首先Access(x),这样x向它的孩子连着的肯定都是虚边,x的子树部分就是x的虚边Splay。
void changetree(int x,tag p){
access(x);
splay(x);
val[x]=atag(val[x],p);
for(int i=2;i<4;i++)if(son[x][i])tagtree(son[x][i],p,1);
up(x);
splay(x);
}
data asktree(int x){
access(x);
splay(x);
data t=data(val[x]);
for(int i=2;i<4;i++)if(son[x][i])t=t+asum[son[x][i]];
return t;
}
信息的和:
对于每个节点x,需要维护一些域:
in:这个点是否是内部点
val:这个点的点权
csum:链上信息和
tsum:子树信息和(不包括链上)
asum:所有信息和
csum[x]=val[x]+csum[son[x][0]]+csum[son[x][1]]
tsum[x]=tsum[son[x][0]]+tsum[son[x][1]]+asum[son[x][2]]+asum[son[x][3]]
asum[x]=csum[x]+tsum[x]
标记:
对于每个节点x,需要维护一些标记:
rev:链翻转标记
ctag:链修改标记
ttag:子树修改标记(不包括链上)
rev和ctag下传方法与Link-Cut Tree一致,
ttag下传方法为:
如果是在实链中的下传,直接下传到ttag,无需修改。
如果是虚边splay中下传到内部点,下传到ttag并修改。
如果是虚边splay中下传到外部点,下传到ttag和ctag并修改。
垃圾回收:
由于add操作会新增大量内部白点,但是内部白点最多同时只有$O(n)$个,所以需要垃圾回收。
效率:
时间复杂度为$O(\log n)$每次操作,但是常数为97,非常大。
#include<cstdio>
#define N 200010
const int inf=~0U>>1;
inline void swap(int&a,int&b){int c=a;a=b;b=c;}
inline int max(int a,int b){return a>b?a:b;}
inline int min(int a,int b){return a<b?a:b;}
inline void read(int&a){
char c;bool f=0;a=0;
while(!((((c=getchar())>='0')&&(c<='9'))||(c=='-')));
if(c!='-')a=c-'0';else f=1;
while(((c=getchar())>='0')&&(c<='9'))(a*=10)+=c-'0';
if(f)a=-a;
}
struct tag{
int a,b;//ax+b
tag(){a=1,b=0;}
tag(int x,int y){a=x,b=y;}
inline bool ex(){return a!=1||b;}
inline tag operator+(const tag&x){return tag(a*x.a,b*x.a+x.b);}
};
inline int atag(int x,tag y){return x*y.a+y.b;}
struct data{
int sum,minv,maxv,size;
data(){sum=size=0,minv=inf,maxv=-inf;}
data(int x){sum=minv=maxv=x,size=1;}
data(int a,int b,int c,int d){sum=a,minv=b,maxv=c,size=d;}
inline data operator+(const data&x){return data(sum+x.sum,min(minv,x.minv),max(maxv,x.maxv),size+x.size);}
};
inline data operator+(const data&a,const tag&b){return a.size?data(a.sum*b.a+a.size*b.b,atag(a.minv,b),atag(a.maxv,b),a.size):a;}
//son:0-1:重链儿子,2-3:AAA树儿子
int f[N],son[N][4],a[N],tot,rt,rub,ru[N];bool rev[N],in[N];
int val[N];
data csum[N],tsum[N],asum[N];
tag ctag[N],ttag[N];
inline bool isroot(int x,int t){
if(t)return !f[x]||!in[f[x]]||!in[x];
return !f[x]||(son[f[x]][0]!=x&&son[f[x]][1]!=x)||in[f[x]]||in[x];
}
inline void rev1(int x){
if(!x)return;
swap(son[x][0],son[x][1]);rev[x]^=1;
}
inline void tagchain(int x,tag p){
if(!x)return;
csum[x]=csum[x]+p;
asum[x]=csum[x]+tsum[x];
val[x]=atag(val[x],p);
ctag[x]=ctag[x]+p;
}
inline void tagtree(int x,tag p,bool t){
if(!x)return;
tsum[x]=tsum[x]+p;
ttag[x]=ttag[x]+p;
if(!in[x]&&t)tagchain(x,p);else asum[x]=csum[x]+tsum[x];
}
inline void pb(int x){
if(!x)return;
if(rev[x])rev1(son[x][0]),rev1(son[x][1]),rev[x]=0;
if(!in[x]&&ctag[x].ex())tagchain(son[x][0],ctag[x]),tagchain(son[x][1],ctag[x]),ctag[x]=tag();
if(ttag[x].ex()){
tagtree(son[x][0],ttag[x],0),tagtree(son[x][1],ttag[x],0);
tagtree(son[x][2],ttag[x],1),tagtree(son[x][3],ttag[x],1);
ttag[x]=tag();
}
}
inline void up(int x){
tsum[x]=data();
for(int i=0;i<2;i++)if(son[x][i])tsum[x]=tsum[x]+tsum[son[x][i]];
for(int i=2;i<4;i++)if(son[x][i])tsum[x]=tsum[x]+asum[son[x][i]];
if(in[x]){
csum[x]=data();
asum[x]=tsum[x];
}else{
csum[x]=data(val[x]);
for(int i=0;i<2;i++)if(son[x][i])csum[x]=csum[x]+csum[son[x][i]];
asum[x]=csum[x]+tsum[x];
}
}
inline int child(int x,int t){pb(son[x][t]);return son[x][t];}
inline void rotate(int x,int t){
int y=f[x],w=(son[y][t+1]==x)+t;
son[y][w]=son[x][w^1];
if(son[x][w^1])f[son[x][w^1]]=y;
if(f[y])for(int z=f[y],i=0;i<4;i++)if(son[z][i]==y)son[z][i]=x;
f[x]=f[y];f[y]=x;son[x][w^1]=y;up(y);
}
inline void splay(int x,int t=0){
int s=1,i=x,y;a[1]=i;
while(!isroot(i,t))a[++s]=i=f[i];
while(s)pb(a[s--]);
while(!isroot(x,t)){
y=f[x];
if(!isroot(y,t)){if((son[f[y]][t]==y)^(son[y][t]==x))rotate(x,t);else rotate(y,t);}
rotate(x,t);
}
up(x);
}
inline int newnode(){
int x=rub?ru[rub--]:++tot;
son[x][2]=son[x][3]=0;in[x]=1;
return x;
}
inline void setson(int x,int t,int y){son[x][t]=y;f[y]=x;}
inline int pos(int x){for(int i=0;i<4;i++)if(son[f[x]][i]==x)return i;return 4;}
inline void add(int x,int y){//从x连出一条虚边到y
if(!y)return;
pb(x);
for(int i=2;i<4;i++)if(!son[x][i]){
setson(x,i,y);
return;
}
while(son[x][2]&&in[son[x][2]])x=child(x,2);
int z=newnode();
setson(z,2,son[x][2]);
setson(z,3,y);
setson(x,2,z);
splay(z,2);
}
inline void del(int x){//将x与其虚边上的父亲断开
if(!x)return;
splay(x);
if(!f[x])return;
int y=f[x];
if(in[y]){
int s=1,i=y,z=f[y];a[1]=i;
while(!isroot(i,2))a[++s]=i=f[i];
while(s)pb(a[s--]);
if(z){
setson(z,pos(y),child(y,pos(x)^1));
splay(z,2);
}
ru[++rub]=y;
}else{
son[y][pos(x)]=0;
splay(y);
}
f[x]=0;
}
inline int fa(int x){//x通过虚边的父亲
splay(x);
if(!f[x])return 0;
if(!in[f[x]])return f[x];
int t=f[x];
splay(t,2);
return f[t];
}
inline int access(int x){
int y=0;
for(;x;y=x,x=fa(x)){
splay(x);
del(y);
add(x,son[x][1]);
setson(x,1,y);
up(x);
}
return y;
}
inline int lca(int x,int y){
access(x);
return access(y);
}
inline int root(int x){
access(x);
splay(x);
while(son[x][0])x=son[x][0];
return x;
}
inline void makeroot(int x){
access(x);
splay(x);
rev1(x);
}
inline void link(int x,int y){
makeroot(x);
add(y,x);
access(x);
}
inline void cut(int x){
access(x);
splay(x);
f[son[x][0]]=0;
son[x][0]=0;
up(x);
}
inline void changechain(int x,int y,tag p){
makeroot(x);
access(y);
splay(y);
tagchain(y,p);
}
inline data askchain(int x,int y){
makeroot(x);
access(y);
splay(y);
return csum[y];
}
inline void changetree(int x,tag p){
access(x);
splay(x);
val[x]=atag(val[x],p);
for(int i=2;i<4;i++)if(son[x][i])tagtree(son[x][i],p,1);
up(x);
splay(x);
}
inline data asktree(int x){
access(x);
splay(x);
data t=data(val[x]);
for(int i=2;i<4;i++)if(son[x][i])t=t+asum[son[x][i]];
return t;
}
int n,m,x,y,z,k,i,ed[N][2];
int main(){
read(n);read(m);
tot=n;
for(i=1;i<n;i++)read(ed[i][0]),read(ed[i][1]);
for(i=1;i<=n;i++)read(val[i]),up(i);
for(i=1;i<n;i++)link(ed[i][0],ed[i][1]);
read(rt);
makeroot(rt);
while(m--){
read(k);
if(k==1){//换根
read(rt);
makeroot(rt);
}
if(k==9){//x的父亲变成y
read(x),read(y);
if(lca(x,y)==x)continue;
cut(x);
link(y,x);
makeroot(rt);
}
if(k==0){//子树赋值
read(x),read(y);
changetree(x,tag(0,y));
}
if(k==5){//子树加
read(x),read(y);
changetree(x,tag(1,y));
}
if(k==3){//子树最小值
read(x);
printf("%d\n",asktree(x).minv);
}
if(k==4){//子树最大值
read(x);
printf("%d\n",asktree(x).maxv);
}
if(k==11){//子树和
read(x);
printf("%d\n",asktree(x).sum);
}
if(k==2){//链赋值
read(x),read(y),read(z);
changechain(x,y,tag(0,z));
makeroot(rt);
}
if(k==6){//链加
read(x),read(y),read(z);
changechain(x,y,tag(1,z));
makeroot(rt);
}
if(k==7){//链最小值
read(x),read(y);
printf("%d\n",askchain(x,y).minv);
makeroot(rt);
}
if(k==8){//链最大值
read(x),read(y);
printf("%d\n",askchain(x,y).maxv);
makeroot(rt);
}
if(k==10){//链和
read(x),read(y);
printf("%d\n",askchain(x,y).sum);
makeroot(rt);
}
}
return 0;
}