2018年国赛高教杯数学建模B题智能RGV的动态调度策略解题全过程文档及程序
2018年国赛高教杯数学建模
B题 智能RGV的动态调度策略
原题再现
图1是一个智能加工系统的示意图,由8台计算机数控机床(Computer Number Controller,CNC)、1辆轨道式自动引导车(Rail Guide Vehicle,RGV)、1条RGV直线轨道、1条上料传送带、1条下料传送带等附属设备组成。RGV是一种无人驾驶、能在固定轨道上自由运行的智能车。它根据指令能自动控制移动方向和距离,并自带一个机械手臂、两只机械手爪和物料清洗槽,能够完成上下料及清洗物料等作业任务(参见附件1)。
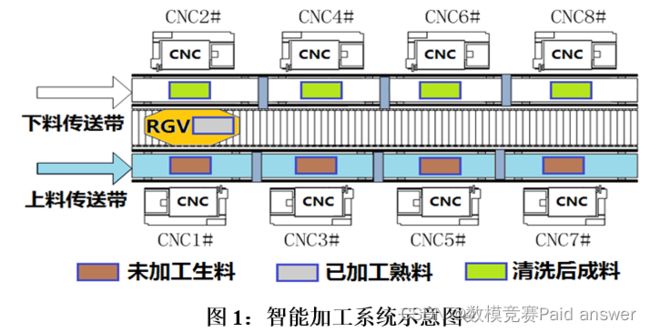
针对下面的三种具体情况:
(1)一道工序的物料加工作业情况,每台CNC安装同样的刀具,物料可以在任一台CNC上加工完成;
(2)两道工序的物料加工作业情况,每个物料的第一和第二道工序分别由两台不同的CNC依次加工完成;
(3)CNC在加工过程中可能发生故障(据统计:故障的发生概率约为1%)的情况,每次故障排除(人工处理,未完成的物料报废)时间介于10~20分钟之间,故障排除后即刻加入作业序列。要求分别考虑一道工序和两道工序的物料加工作业情况。
请你们团队完成下列两项任务:
任务1:对一般问题进行研究,给出RGV动态调度模型和相应的求解算法;
任务2:利用表1中系统作业参数的3组数据分别检验模型的实用性和算法的有效性,给出RGV的调度策略和系统的作业效率,并将具体的结果分别填入附件2的EXCEL表中。
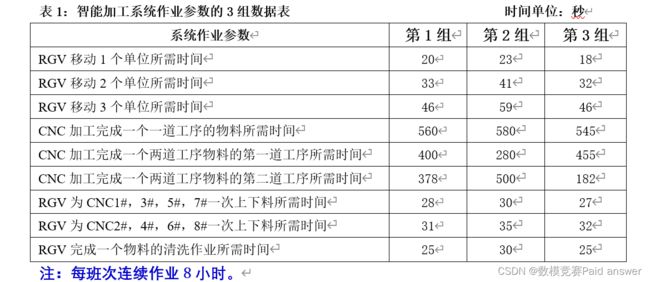
附件1:智能加工系统的组成与作业流程
附件2:模型验证结果的EXCEL表(完整电子表作为附件放在支撑材料中提交)
整体求解过程概述(摘要)
本文对智能加工系统中 RGV 的动态调度优化问题进行研究。
针对任务一,我们首先对系统进行分析,给出了几个重要定义和优化指导原则,例
如 RGV 工作循环定义、系统效率均衡原则、CNC 满载工作上限等。同时,给出了相关
分析和证明,包括在一定条件下的 RGV 循环的最短用时证明,系统最优上限的证明等。
这些理论为我们建立最优化模型和模型评估指标提供了依据。
对于情景一,我们对原有模型进行转化,将其转化为时间维度上的多队列任务调度
优化模型,并基于事件对时间进行离散化,为减少迭代步数,根据划分结果构建最优状
态转移图模型,利用状态向量和状态转移矩阵完成系统工作的模拟和决策优化。考虑到
求解该优化问题计算开销较大,采用多阶段决策模型进行求解,即将最优状态转移图模
型中的优化原则结合已明确的优化准则构建各个阶段的决策方案,从而完成问题的求
解,得到在 8 个小时内三组参数下系统可产生最大熟料数量分别为 382、359、391;经
检验,在求解效率和求解质量上都达到了很好的效果。
对于情景二,我们分析了两类 CNC 在系统中共存时产生的复杂约束情况,结合系
统效率均衡对应系统整体较大效率的规律,近似确定了两种 CNC 的数量比例。再通过
搜索找到了最优的 CNC 空间排布方案,从而建立带工序约束的最优状态转换图模型。
在求解时,通过改进的状态转移优化准则对模型进行求解,得到在该约束条件下,8 个
小时内三组参数下系统可产生最大熟料数量分别为 253、210、240;
对于情景三,需要引入了负载因子进行了故障的随机模拟。该过程的本质是在状态
转移时引入不确定性。由此引入新的变量,对状态转移矩阵和转移约束进行拓展补充,
并对评价函数进行修正,从而建立了带有故障风险的最优状态转换图模型。在使用多阶
段决策求解时,除了追求完成物料数最大,还要保持系统内两类 CNC 工作能力均衡以
取得更高的工作效率。由于情况较多,结果可见附件 Excel。
针对任务二,我们结合证明的结论,构建了结果偏差率计算公式,并为该标准提供
了必要的理论支持,具有较高参考意义。经过验证,模型求解算法结果与最优解有很好
的近似。针对系统效率,我们构建了系统效率评价指标,用于刻画系统整体效率与各部
分效率均衡情况。
模型假设:
1. 假设 RGV 足够智能,可在未收到需求信号时主动移动到指定 CNC 位置处;此外,自动引导车可在收到指令后维持在在原地停止等待状态;
2. 假设 RGV 足够智能且可以 CNC 通讯,可以获取 CNC 的加工完成剩余时间以及当前班次剩余时间信息;
3. 假设上料带具有理想上料速率,即:RGV 为 CNC(或加工第一道工序的 CNC)上生料时,其传送带保证 CNC 前方总有所需生料;
4. 假设下料带具有理想下料效率,不会在 RGV 下料时,出现下料带堵塞的问题;
5. 假设除了 CNC 在加工过程中可能发生故障外,其他部件都不发生意外和磨损,且可在指定时间准时完成相应操作。
问题分析:
问题一分析
该问题要求根据一般问题,给出 RGV 动态调度模型和相应的求解算法。针对该问题,首先需要对该系统的运行特点进行一定的抽象、概括和证明,例如:在最优的调度策略下各部分机器效率应当均衡的。这些规则将用于构建 RGV 动态调度模型。
针对情况 1,结合对系统分析的结果,可以将 8 个 CNC 转换为 8 个工作队列,将物料加工作业抽象为队列中的事件,则题目第一问可以转换为完成队列中带约束条件的任务最优调度。转换完成后,可从时间维度对系统基于事件进行状态划分。基于该状态划分结果,可以构建最优状态转移图(有向有权图)模型,其中带权节点代表 CNC 的处理时间、带权有向边带代表 RGV 将清洗工作、停止等待以及移动所需要的时间,由此构建状态向量和状态转移矩阵。该模型以最大化有限时间内完成的熟料数目最多为目标,而约束则可引入总工时约束、物料加工用时约束、RGV 运动时间的约束等。此外,该问题还可以从建立物料数目确定,最小化时间的角度考虑建立相应最优化模型等。最优状态转移图模型的化简工作可以考虑以两无权点及该两点所确定的一条带权有向边代替原来的带权点,从而完成对模型的构建和化简。
针对情况 2,我们可以建立带有工序约束的最优状态转移模型。该模型依然是基于系统状态转移的思想,可以证明工序一、二紧邻是系统高效率的指导原则,我们修改状态转移矩阵的约束条件,限制状态向量的转移方向从而完成问题的求解。最优化目标依然是在有限时间内最大化生产熟料数目。
针对情况 3,我们可以在最优状态转移图模型和带有工序约束的最优状态转移模型的基础上引入突发事件随机变量,通过引入该随机变量限制部分状态的转移效果,同时引入等待时间变量,从而完成问题模型的建立。对于算法的求解可以采用引入剪枝规则、回溯法、分支限界法等。值得注意的是,在该求解该模型时,分支限界法求解目标则是尽快找出满足约束条件的一个解,或在满足约束条件的解中找出在某种意义下的最优解,更适合求解离散最优化问题。但是,考虑到即使引入剪枝策略等模型求解的时间和空间复杂度可能较大,因此在求解算法时采用分阶段优化的策略完成模型的求解,同时采用基于事件的时间离散化处理,最后可以对结果进行分析比较,作为模型的近似解。除此之外,在该类最优化问题求解时,也可以采用混合遗传算法 [1]、禁忌搜索算法 [2] 等。
问题二分析
该问题可以通过输入题目提供的数据检验模型的实用性和算法的有效性,并对结果和系统基本上限进行比较,判断模型和算法的实用性和有效性,同时输出该过程中 RGV的调度策略。对于系统的作业效率,可以定义系统工作效率为系统中 CNC 的工作时间在一个工时内比例。此外,可从系统工作效率均衡的角度分析模型实用性和算法的有效性。
模型的建立与求解整体论文缩略图
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
The actual procedure is shown in the screenshot
1 #include <iostream>
2 #include <algorithm>
3 #include <vector>
4 #include <map>
5 using namespace std;
6 typedef pair<int, int> pii;
7 typedef pair<pii, vector<int>> piv;
8
9 const int mov_t[] = {0, 20, 33, 46};
10 const int proc_t[] = {560, 400, 378};
11 const int ud_t[] = {28, 31};
12 const int clr_t = 25;
13 const int tot_t = 1000;
14
15 vector<piv> dfs_stack, ans_stack;
16 int global_ans = 0;
17
18 void print_st(piv& st) {
19 cout << st.first.first << ' ' << st.first.second;
20 for (int i : st.second) {
21 cout << ' ' << i;
22 }
23 cout << endl;
24 }
25
26 void print_stack() {
27 for (auto& st : ans_stack) {
28 print_st(st);
29 }
30 }
31
32 int eval_func(int rem_t, int cur_pos, vector<int>& cnc_sts) {
33 int res = 0;
34 rem_t −= mov_t[cur_pos];
35 if (rem_t < 0) rem_t = 0;
36 for (int i = 0; i < 8; i++) {
37 if (cnc_sts[i] != −1 && rem_t >= cnc_sts[i]) {
38 res++;
39 }
40 }
41 res += rem_t *8 / (proc_t[0] + ud_t[0]);
42 return res;
43 }
44
45 void dfs(int rem_t, int cur_pos, vector<int> cnc_sts, int cur_ans) {
46 if (cur_ans + eval_func(rem_t, cur_pos, cnc_sts) <= global_ans) return;
47 if (rem_t <= mov_t[cur_pos]) {
48 if (cur_ans > global_ans) {
49 global_ans = cur_ans;
50 ans_stack = dfs_stack;
51 }
52 return;
53 }
54 dfs_stack.push_back(make_pair(make_pair(rem_t, cur_pos), cnc_sts));
55 vector<int> order = {0, 1, 2, 3, 4, 5, 6, 7};
56 for (int i = 0; i < 8; i++) {
57 int cur_max = i;
58 for (int j = i; j < 8; j++) {
59 if (max(mov_t[abs(cur_pos − order[cur_max] / 2)],
cnc_sts[order[cur_max]]) + ud_t[order[cur_max] % 2] <
max(mov_t[abs(cur_pos − order[j] / 2)], cnc_sts[order[j]]) +
ud_t[order[j] % 2]) {
60 cur_max = j;
61 }
62 }
63 swap(order[cur_max], order[i]);
64 }
65 for (int i : order) {
66 int pos = i / 2;
67 int t = max(mov_t[abs(cur_pos − pos)], cnc_sts[i]) + ud_t[i % 2];
68 vector<int> new_cnc_sts = cnc_sts;
69 new_cnc_sts[i] = proc_t[0] − (cnc_sts[i] == −1 ? 0 : clr_t);
70 for (int j = 0; j < 8; j++) if(i != j) {
71 if (new_cnc_sts[j] == −1) continue;
72 new_cnc_sts[j] −= t + clr_t;
73 if (new_cnc_sts[j] < 0) new_cnc_sts[j] = 0;
74 }
75 dfs(rem_t − t − clr_t, pos, new_cnc_sts, cur_ans + (cnc_sts[i] == −1 ? 0 :
1));
76 }
77 dfs_stack.pop_back();
78 }
79
80 int main() {
81 ios::sync_with_stdio(false);
82 vector<int> init_st = {−1, −1, −1, −1, −1, −1, −1, −1};
83 dfs(tot_t, 0, init_st, 0);
84 cout << global_ans << endl;
85 print_stack();
86 return 0;
87 }
1 import random
2
3 move_step_times = [0, 20, 33, 46]
4 process_times = [560, 400, 378]
5 up_down_times = [28, 31]
6 clean_time = 25
7
8 # move_step_times = [0, 23, 41, 59]
9 # process_times = [580, 280, 500]
10 # up_down_times = [30, 35]
11 # clean_time = 30
12
13 # move_step_times = [0, 18, 32, 46]
14 # process_times = [545, 455, 182]
15 # up_down_times = [27, 32]
16 # clean_time = 25
17 # INF = 100000000
18
19 cur_pos = 0
20 cur_time = 0
21
22 def move_time(pos1, pos2):
23 return move_step_times[abs(pos1 − pos2)]
24
25 cnt = 0
26 res = 0
27 cnc_states = [0 for i in range(8)]
28 fst_time = [True for i in range(8)]
29 item_idx = [−1 for i in range(8)]
30 broken = [0 for i in range(8)]
31 items = []
32 broken_items = []
33
34 while True:
35 candidates = [i for i in range(8)]
36 candidates.sort(key=lambda i:max(move_time(cur_pos, i // 2), cnc_states[i]) +
up_down_times[i % 2])
37 ok = False
38 for cur_cnc in candidates:
39 t1 = max(move_time(cur_pos, cur_cnc // 2), cnc_states[cur_cnc])
40 to_cur_cnc_time = t1 + up_down_times[cur_cnc % 2]
41 ct = clean_time if not fst_time[cur_cnc] else 0
42 if cur_time + to_cur_cnc_time + ct + move_time(cur_pos, 0) > 8 *3600:
43 continue
44 ok = True
45 # print(cur_time, cur_pos, cnc_states, res)
46 if broken[cur_cnc] > 0:
47 continue
48 if random.random() < 0.01:
49 broken[cur_cnc] = random.randint(10 *
60, 20 *60)
50 items.append({'cnc': cur_cnc + 1, 'up_time': cur_time + t1, 'down_time':None})
51 print(len(items), cur_cnc + 1, cur_time + to_cur_cnc_time, cur_time +broken[cur_cnc])
52 broken_items.append({'cnc': cur_cnc + 1, 'up_time': cur_time + t1,'down_time': None})
53 continue
54 for i in range(8):
55 cnc_states[i] −= to_cur_cnc_time + ct
56 broken[i] −= to_cur_cnc_time + ct
57 if cnc_states[i] < 0:
58 cnc_states[i] = 0
59 if broken[i] < 0:
60 broken[i] = 0
61 items.append({'cnc': cur_cnc + 1, 'up_time': cur_time + t1, 'down_time':None})
62 cnc_states[cur_cnc] = process_times[0] − ct
63
64 if fst_time[cur_cnc]:
65 fst_time[cur_cnc] = False
66 else:
67 res += 1
68 items[item_idx[cur_cnc]]['down_time'] = cur_time + t1
69 cur_time += to_cur_cnc_time + ct
70 cur_pos = cur_cnc // 2
71 item_idx[cur_cnc] = len(items) − 1
72 break
73 if not ok:
74 break
75 print(res)
76 print(res *process_times[0] / (8 *8 *3600))
77 for item in items:
78 print('\t'.join(map(str, item.values())))
79 print('Broken:')
80 for item in broken_items:
81 print('\t'.join(map(str, item.values())))
82 print(items)

