代码随想录算法训练营第五十九天| 503. 下一个更大元素 II、42. 接雨水。
503. 下一个更大元素 II
题目链接:力扣
题目要求:
给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1 。
示例 1:
输入: nums = [1,2,1] 输出: [2,-1,2] 解释: 第一个 1 的下一个更大的数是 2; 数字 2 找不到下一个更大的数; 第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
1 <= nums.length <= 104-109 <= nums[i] <= 109
总结:
本题的大概思路实际上和上两题的思路大差不差,区别就是,这里每次下一个的最大元素,可以反过来再从前面的找,它是一个循环的数组,那我们就把遍历的范围扩大到原来的两倍,然后大出的部分取模运算,就可以达到再次遍历之前元素的效果,最终返回的result数组大小还是一倍的大小。但是,每个位置的结果,可能就是该位置之前的元素值了,因为i取的范围是两倍的大小。
class Solution {
public int[] nextGreaterElements(int[] nums) {
int len = nums.length;
int[] result = new int[len];
Arrays.fill(result,-1);
Stack stack = new Stack<>();
stack.push(0);
for(int i = 1;i < 2*len;i++){
if(nums[i % len] <= nums[stack.peek()]){
stack.push(i % len);
}else{
while(!stack.isEmpty() && nums[i % len] > nums[stack.peek()]){
result[stack.peek()] = nums[i % len];
stack.pop();
}
stack.push(i % len);
}
}
return result;
}
} 42. 接雨水
题目链接:力扣
题目要求:
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
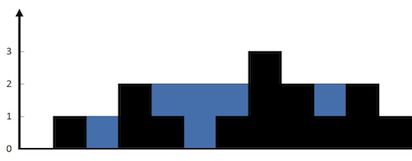
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
总结:
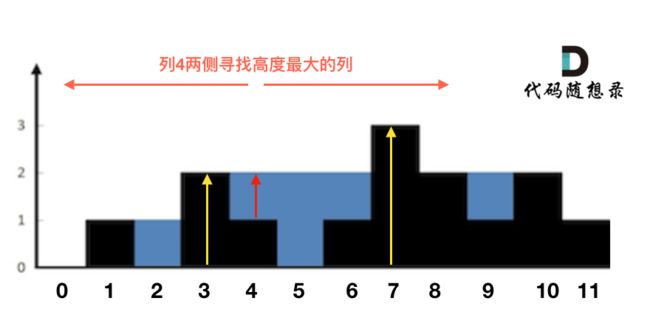
例如求列4的雨水高度,如图:
列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
列4 右侧最高的柱子是列7,高度为3(以下用rHeight表示)。
列4 柱子的高度为1(以下用height表示)
那么列4的雨水高度为 列3和列7的高度最小值减列4高度,即: min(lHeight, rHeight) - height。
列4的雨水高度求出来了,宽度为1,相乘就是列4的雨水体积了。
此时求出了列4的雨水体积。
一样的方法,只要从头遍历一遍所有的列,然后求出每一列雨水的体积,相加之后就是总雨水的体积了。
首先从头遍历所有的列,并且要注意第一个柱子和最后一个柱子不接雨水
如果每次遍历一个位置i,再求其两边的的最大高度,复杂度为n的平方,超时了,所以需要在遍历前就把每个位置的最左高度,和最右高度求出来,用leftmax[i]数组代表每一个i位置的左边最大高度,right[i]数组代表每个i位置的右边的最大高度,比如说位置4的左边最大高度就为,位置3的左边最大高度与位置3的高度取最大值,位置4的右边最大高度就为,位置5的右边最大高度与位置5的高度取最大值。得到每个位置的左边最大高度和右边最大高度后,再开始遍历每列的水的体积,等于该位置左边最大高度和右边最大高度取最小值,然后再减去本位置的高度,如果这个值是个大于0的值,因为长度是1,所以体积与这个值是一样的,直接把这一列的体积累加到sum去,最终遍历完所有的列,返回最终水的总体积sum即可。
class Solution {
public int trap(int[] height) {
int len = height.length;
if(height.length <= 2) return 0;
int[] leftmax = new int[len];
int[] rightmax = new int[len];
leftmax[0] = 0;
for(int i = 1;i < len;i++){
leftmax[i] = Math.max(leftmax[i-1],height[i-1]);
}
rightmax[len - 1] = 0;
for(int i = len - 2;i >= 0;i--){
rightmax[i] = Math.max(rightmax[i+1],height[i+1]);
}
int sum = 0;
for(int i = 1;i < len - 1;i++){
int count = Math.min(leftmax[i],rightmax[i]) - height[i];
if(count > 0) sum += count;
}
return sum;
}
}