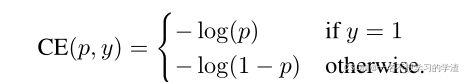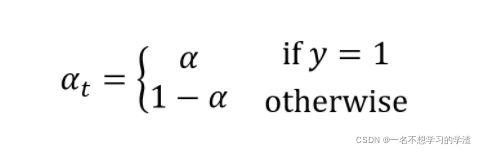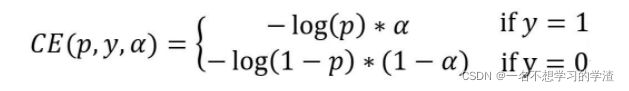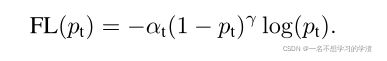目标检测中Focal loss 损失函数理论和代码（Pytorch）学习笔记分享

相信大家都知道，Focal loss是被应用在Retinanet目标检测中的，也使单阶段（Retinanet）目标检测的效果超过了双阶段（Faster_Rcnn）目标检测。

一、在学习之前，首先了解一下正负样本的概念：

正样本：就是网络需要去学习的样本，比如我们需要在一张图片上识别汽车，那么汽车就是正样本。

负样本：为了让网络泛化性能更强的无关样本。比如我们需要在一张图片上识别汽车，那么图片中的马就是负样本。

难样本：就是非常难识别的样本，比如我们需要在一张图片上识别猫咪（正样本），那么有一只长得像猫的老虎就是难样本（也称为难负样本），那么有一个长的像老虎的猫，也叫难样本（但是叫做难正样本），这一块比较难理解，大家可以好好读读这句话！

二、二元交叉熵损失函数的认识

 学到这里，大家应该都是学过二分类的算法，对于二元交叉熵，都是比较熟悉的。

 二元交叉熵损失函数

如下图，是二元交叉熵的另外写法，当我们的标签y=1，那么我们的损失函数就是-log(p)，其中p表示网络预测为正样本的概率，反之则为-log(1-p)。

 二元交叉熵损失函数的另外写法

为了更加方便（其实我觉得不方便，感觉就是套娃，但是论文非这样弄，所以就展示出来）：

 因此二元交叉熵损失函数的写法又变成下图所示：

三、为什么需要Focal loss? 

 大家都知道，单阶段的目标检测的精确度和召回率一直都是不如双阶段目标检测算法（虽然速度比双阶段目标检测快），这里面的理由是什么呢？这里何凯明大神的团队就声明：因为单价段目标检测的锚框太多了，也就是有太多的负样本，我们举个例子，相信大家学过yolov3，yolov3的输出特征图大小分别是13x13、26x26,52x52，那么每个特征图的每个格子都有三个锚框,那么一共有13x13x3+26x26x3+52x52x3=9387个样本（包含正负样本），但是里面的正样本只有1之5个，其余都是负样本，虽然有些人将这个正负样本的比例进行了修正，结果也得到了相应的提升，但是效果还是不如双阶段目标检测算法，双阶段目标检测算法，首先会生成大学2000个候选框，这些样本（候选框）在一定的程度上都是有效的，很好的区分了前景和背景信息。然后再对这些候选框进行分类和回归预测。从而效果比单阶段目标检测好。

四、如何改进的呢？

至此，就引出了我们的Focal loss, Focal loss从两方面进行了改进：

1、控制正负样本的权重 （Balanced Cross Entropy ）             

2、控制容易分类和难分类样本的权重

控制正负样本的权重（Balanced Cross Entropy ） ：   

由上面我们得到了 二元交叉熵损失函数的变形体：

那么 Focal loss首先在公式中添加了一个参数，如下图：

其中： 

 当标签y=1时，那么代表是预测正样本，可以通过α来正样本控制该损失值的比例，反之，也可以控制负样本的损失值的比例。

控制容易分类和难分类样本的权重

在密集探测器的训练过程中遇到的大类不平衡压倒了交叉熵损失。容易分类的负片构成了大部分损失，并主导了梯度。虽然上面的α平衡了正面/负面例子的重要性，但它没有区分简单/困难的例子。

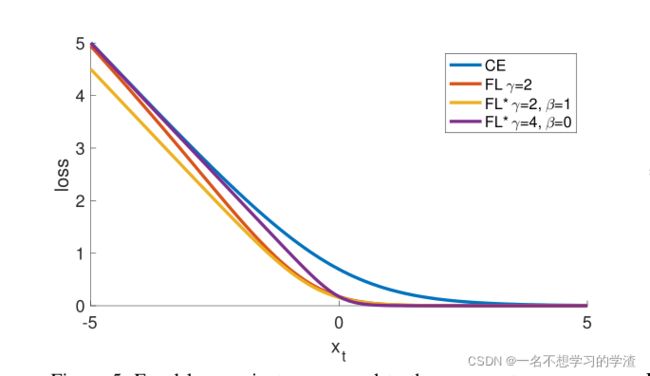
 从上面的图中可以看出，在一般的二元损失函数的曲线中（蓝线），对于容易区分的正负样本内，它的损失函数的值还是比较大，这就是因为一些无效的样本太多，虽然一个样本的损失值很小，但是很多个样本的损失值就会变得非常大。所以就提出了一种参数来控制这样的损失函数：

 大家可以看上图，当标签y=1时，预测值趋向1时，那么（1-pt）---->0从而达到降低易区分样本的比例，那么有人就会说，当预测值为趋向1时，log(pt)----->0，不也能达到同样的效果吗？其实这个问题我也想过，我想是因为这个原因，大家想一下，0.02是不是很小，那么0.02*0.02是不是更小，而上面的公式就可以想象成这个效果。如果有不对的地方，欢迎大家指正！

在实践中，我们加上了αt构成了完整的损失函数：

import numpy as np
import torch.nn as nn
import math
gt=[1,0,1,0]
pre=[0.95,0.05,0.5,0.5]#前面两个是易区分样本，后面两个为难样本
a=0.25
weight=[a if y==1 else (1-a) for y in gt]
print(weight)
#我们另t=2
t=2
for i in range(len(gt)):
    if gt[i]==1:
        print(-((1-pre[i])**t)*math.log(pre[i])*weight[i])
    else:
        print(-((pre[i])**t)*math.log(1-pre[i]) * weight[i])

得到的结果为：

 从结果可以看出，对于容易区分的样本，确实将比例降低了，并且随着超参数的设置，降低的比例还是不同的，但是这个超参数也不能随便设置，想要结果好，那么合适超参数必须要有。

 不同的超参数得到了不同的损失函数