【多目标进化优化】MOPSO 原理与代码实现

博主相信： 有足够的积累，并且一直在路上，就有无限的可能！！！

‍个人主页： 青年有志的博客

Gitee 源码地址： https://gitee.com/futurelqh/Multi-objective-evolutionary-optimization

---

前言

前驱知识

• 粒子群优化算法 PSO：https://blog.csdn.net/qq_46450354/article/details/127464089
• Pareto 最优解集： https://blog.csdn.net/qq_46450354/article/details/127917026

粒子群优化算法 PSO

pbest： 粒子本身经历过的最优位置

gbest： 粒子群整体经历过的最优位置

算法思路： 在单目标优化中，通过自我认知 pbest 以及社会认知 gbest 来计算出每个个体下一次移动的速度，从而更新个体所处的位置 x，并更新个体 pbest，以及群体的 gbest，更新的依据直接通过比较目标函数值 function value 的大小即可。

PSO 算法流程图

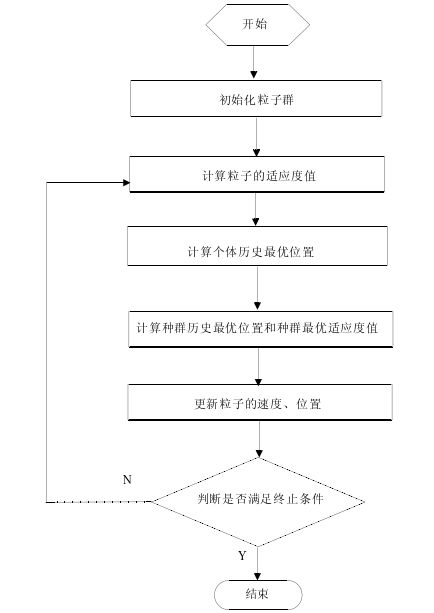
PSO 引出 MOPSO

• PSO 在用于单目标优化过程中，由于只有一个函数，两个个体之间可以通过直接比较大小来判断好坏，从而判断是否更新 pbest，gbest。
• 在多目标问题中存在多个目标值，比如求两个目标函数的最小值，有两个个体 $P_1=(8,15),P_2=(10,12)$，$P_1$ 的第一个目标函数值小于 $P_2$，而第二个目标函数值大于 $P_2$，如何判断谁更好呢？

问题：

1. 如何更新多目标中的 pbest ？
2. 如何更新多目标中的 gbest ？
3. 对于多目标优化问题，输出的结果为一个集合，即 rep (非支配集/归档集) ，此集合的大小如何维护 ？
4. 并且 PSO 很容易陷入局部最优，如何避免呢？

注： rep 集，在部分文献中会称为 Archive 集，均为同一种，即当前迭代中的的非支配集，也称为归档集，为避免混淆，本文同一使用 rep 。

MOPSO 所解决的正是这些个问题，从而将单目标 PSO，变为了能够高效求解多目标优化的算法。下面我们来看看这些问题是如何解决的

1. 如何更新多目标中的 pbest ？

分为三种情况进行更新：

• ① 当新产生的个体 i 在每个目标函数值上都比 pbest 更优越，则更新 pbest （i 支配 pbest）
• ② 当新产生的个体 i 在每个目标函数值上都比 pbest 更劣，则不更新 （pbest 支配 i）
• ③ 当新产生的个体 i 在部分目标函数值上比 pbest 优越，则随机按照一定的概率进行更新 （i 与 pbest 互不支配）

2. 如何更新多目标中的 gbest ？

• 如何在所有互不支配的个体当中选出这个 leader 个体呢？ 这就需要引入自适应网格算法了

自适应网格算法

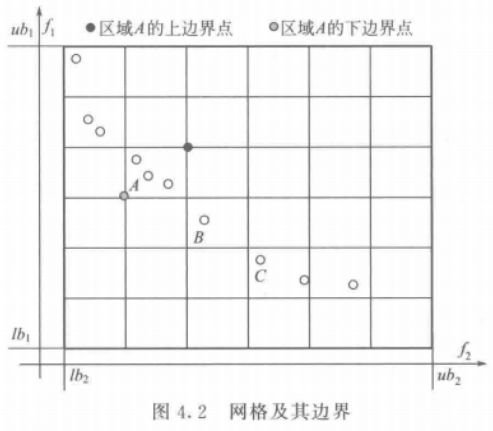
       ~~~~~~        算法思路： 将所有个体划分在不同的网格里面，再计算网格的密度，密度越小的网格，粒子越稀疏，个体被选择的概率越大（从而保证粒子的分布性）。具体步骤如下：

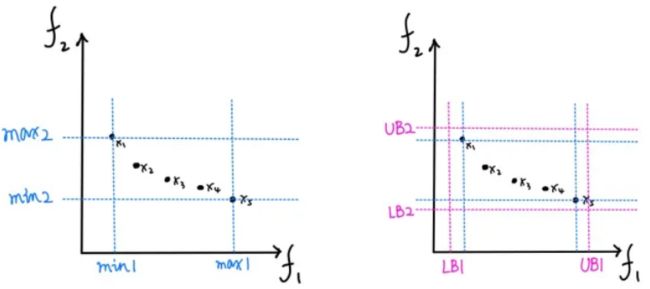
Step1： 遍历集合种群中的所有个体，分别在每一个目标函数上找出所有个体中的最小值和最大值，如图所示，获得目标函数 $f_1$ 上的最小值 $mi{n}_1$、最大值 $ma{x}_1$，以及目标函数 $f_2$ 上的最小值 $mi{n}_2$、最大值 $ma{x}_2$。为了保证边界粒子 $x_1、x_5$ 也能在网格内，需要进行延长操作，把最大最小值根据一定比例稍微延长一点，最后获得网格的边界 $L{B}_1、U{B}_1、L{B}_2、U{B}_2$

Step2： 假设设置的参数 n = 3，将网格平均切割成 3 X 3 = 9 个格子

Step3： 摘选出其中有个体的网格，并计算这些网格中存储的个体总数，如：① = 1，② = 1，③ = 1，④ = 2

Step4： 由前面获得的个体数根据公式计算这些网格的被选概率，个体越少被选概率越大，归一化所有网格的被选概率和为 1。

Step5： 根据前面计算的概率，采取轮盘赌方法选择一个网格，该网格中的个体作为 gBest 备选集，在备选集中采用随机选择的方法选择其中一个个体作为全局最优 gBest

3. 如何维护 rep （非支配集/归档集) ？

• 同样可以采取自适应网格算法。即假设在加入新的非支配个体后，rep 库现在的长度是 $m(m>N)$，此时我们需要删除 $m-N$ 个个体来保证 rep 不溢出。此时只需要通过自适应网格法从 rep 库中选择出一个最差劲个体然后从rep库中删除，如此循环 $m-N$ 次，问题迎刃而解

MOPSO 进行了三轮筛选

1. 首先，根据支配关系进行第一轮筛选，将个体自身与上一次相比的劣解去除，即更新 pbest

2. 将所有个体根据支配关系进行第二轮筛选，将劣解去除，并加入到 rep 归档集中，并计算个体所处的网格位置

3. 最后，若归档集数量超过了存档阀值，则根据自适应网格进行筛选删除，直到阀值限额为止，重新进行网格划分。

4. 如何避免算法陷入局部最优？

Step1： 对当前的粒子 x，根据当前迭代次数 It 和最大迭代次数 MaxIt 以及突变率 m 计算扰乱算子 p。

$$p=(1-\frac{(It-1)}{(MaxIt-1)}{)}^{(1/m)}$$

Step2： 获取随机数 rand，如果 rand < p，随机选择粒子的某个决策变量进行变异，其余决策变量不变；若 rand 不小于 p，则保持不变。

Step3： 如果粒子需要变异，首先随机选择到粒子 x 的第 j 个决策变量 x(j)，然后根据扰乱算子计算变异范围 d，

$$d=p\ast (VarMax-VarMin);$$

式中，$VarMax$ 和 $Varmin$ 分别是规定的决策变量的最大值和最小值。

Step4： 由 d 计算变异的上下界，上界 $UB=x(j)+d$，下界 $LB=x(j)-d$。同时注意越界处理：
$$UB=min(UB,Va{r}_{max}),LB=max(LB,Va{r}_{min})$$

Step5： 最后根据变异的范围 $[LB,UB]$ 随机获取新的 $x(j)=unifrnd(lb,ub)$ ，即获得区间 $(lb,ub)$ 中的一个随机数。

Step6： 在粒子变异后，要比较变异后的粒子是否更优秀，如果变异后的粒子更优秀则更新粒子，否则不更新；同样还要比较新的粒子和粒子的 pBest，若新的粒子比 pBest 优秀则更新 pBest，否则不更新。

算法流程

综上可知 MOPSO 算法主要是针对以下一些问题进行研究：

1. 如何选择 pbest。对于多目标来说两个粒子的对比，并不能对比出哪个好一些。如果粒子的每个目标都要好的话，则该粒子更优。若有些更好，有些更差的话，就无法严格的说哪个好些，哪个差一些。

2. 如何选择 gbest。对于多目标来说，最优的个体有很多个。该如何选择，涉及到最优个体的存档、存档的管理等问题（多样性/分布性）

3. 速度更新公式优化；

4. 位置更新处理；

5. 增加扰乱算子即变异算子的选择问题，主要是为了解决 PSO 快速收敛到局部最优的问题，增加扰乱可以使得收敛到全局最优

6. 增加一些其他的操作来改善收敛性和多样性

补充

• 上述解决方案为较简单的方式，还可以有其他很多方式来解决这三类问题，从而实现不同的算法。

MOPSO 做出的改进方向如下：

1. 速度更新公式的优化，如：引入了一个收缩因子等

2. 解决算法快速收敛陷入局部最优的问题，如：变异操作

3. 算法收敛性和多样性的实现方式，如本文的自适应网格算法；

4. MOPSO 的存档方法

算法执行图

算法在 ZDT1 测试函数下的执行结果

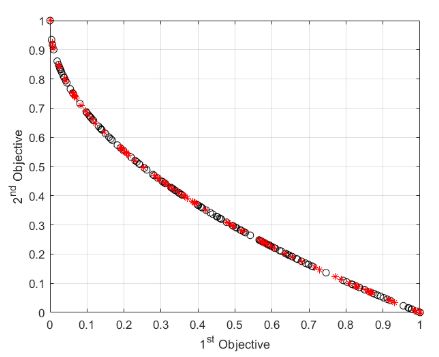
利用综合指标 （HV、IGD） 测试算法在测试函数上的收敛性与分布性，在迭代完成后加上下面两段代码即可：

zdt1.mat：为测试函数 zdt1 的真是 Pareto 解集，在文章开头给出的 Gitee 地址中有

load('zdt1.mat'); % 真实 Pareto 解集
HVResult = HV([rep.Cost]', zdt1)
IGDResult = IGD([rep.Cost]', zdt1)

代码实现

mopso.mlx

Problem Definition

CostFunction = @(x) ZDT(x);      % Cost Function

nVar = 5;             % Number of Decision Variables

VarSize = [1 nVar];   % Size of Decision Variables Matrix

VarMin = 0;          % Lower Bound of Variables
VarMax = 1;          % Upper Bound of Variables

MOPSO Parameters

MaxIt = 200;           % Maximum Number of Iterations

nPop = 200;            % Population Size

nRep = 100;            % Repository Size

w = 0.5;              % Inertia Weight
wdamp = 0.99;         % Intertia Weight Damping Rate
c1 = 1;               % Personal Learning Coefficient
c2 = 2;               % Global Learning Coefficient

nGrid = 7;            % Number of Grids per Dimension
alpha = 0.1;          % Inflation Rate

beta = 2;             % Leader Selection Pressure
gamma = 2;            % Deletion Selection Pressure

mu = 0.1;             % Mutation Rate

Initialization

empty_particle.Position = [];
empty_particle.Velocity = [];
empty_particle.Cost = [];
empty_particle.Best.Position = [];
empty_particle.Best.Cost = [];
empty_particle.IsDominated = [];
empty_particle.GridIndex = [];
empty_particle.GridSubIndex = [];

pop = repmat(empty_particle, nPop, 1);

for i = 1:nPop
    
    pop(i).Position = unifrnd(VarMin, VarMax, VarSize); % 产生范围内的连续随机数
    
    pop(i).Velocity = zeros(VarSize);
    
    pop(i).Cost = CostFunction(pop(i).Position);
    
    
    % Update Personal Best
    pop(i).Best.Position = pop(i).Position;
    pop(i).Best.Cost = pop(i).Cost;
    
end

% Determine Domination
pop = DetermineDomination(pop);

rep = pop(~[pop.IsDominated]); % 选出当前非支配个体

Grid = CreateGrid(rep, nGrid, alpha); % 定义网格

for i = 1:numel(rep)
    rep(i) = FindGridIndex(rep(i), Grid); % 给每个个体分配网格位置
end

MOPSO Main Loop

for it = 1:MaxIt
    
    for i = 1:nPop
        
        leader = SelectLeader(rep, beta); % 轮盘赌选择 gbest
        
        pop(i).Velocity = w*pop(i).Velocity ...
            +c1*rand(VarSize).*(pop(i).Best.Position-pop(i).Position) ...
            +c2*rand(VarSize).*(leader.Position-pop(i).Position);
        
        % 更新位置
        pop(i).Position = pop(i).Position + pop(i).Velocity;
        
        % 越界判断
        pop(i).Position = max(pop(i).Position, VarMin);
        pop(i).Position = min(pop(i).Position, VarMax);
        
        % 计算新的目标值
        pop(i).Cost = CostFunction(pop(i).Position);
        
        if Dominates(pop(i), pop(i).Best) % 如果 i 支配 Best，则更新 Best
            pop(i).Best.Position = pop(i).Position;
            pop(i).Best.Cost = pop(i).Cost;
            
        elseif Dominates(pop(i).Best, pop(i)) % 若 Best 支配 i ，则不更新
            % Do Nothing
            
        else % 若互不支配，则产生随机数判断是否更新
            if rand<0.5
                pop(i).Best.Position = pop(i).Position;
                pop(i).Best.Cost = pop(i).Cost;
            end
        end
        
    end
    
    % Add Non-Dominated Particles to REPOSITORY
    rep = [rep
         pop(~[pop.IsDominated])]; %#ok
    
    % Determine Domination of New Resository Members
    rep = DetermineDomination(rep);
    
    % Keep only Non-Dminated Memebrs in the Repository
    rep = rep(~[rep.IsDominated]);
    
    % Update Grid
    Grid = CreateGrid(rep, nGrid, alpha);

    % Update Grid Indices
    for i = 1:numel(rep)
        rep(i) = FindGridIndex(rep(i), Grid);
    end
    
    % Check if Repository is Full
    if numel(rep)>nRep
        
        Extra = numel(rep)-nRep;
        for e = 1:Extra
            rep = DeleteOneRepMemebr(rep, gamma);
        end
        
    end
    
    % Plot Costs
    figure(1);
    PlotCosts(pop, rep);
    pause(0.01);
    
    % Show Iteration Information
    disp(['Iteration ' num2str(it) ': Number of Rep Members = ' num2str(numel(rep))]);
    
    % Damping Inertia Weight
    w = w*wdamp;
    
end

ZDT.m：测试函数 ZDT1

function z = ZDT(x)
% Function: z = ZDT(x)
%
% Description:  此系列的测试函数总共有 6 个，ZDT1 ~ ZDT6, 属于数值型测试函数，
%               当前实现的测试函数为 ZDT1
%
%
% Syntax:
%   
%
% Parameters:
%   x：决策变量
%
% Return:
%   z：函数结果 f1, f2
%
%                  Young99
%         Revision:    Data: 
%*************************************************************************

    n = numel(x);

    f1 = x(1);
    
    g = 1+9/(n-1)*sum(x(2:end));
    
    h = 1-sqrt(f1/g);
    
    f2 = g*h;
    
    z = [f1
       f2];

end

DetermineDomination.m：判断是否为非支配个体

function pop = DetermineDomination(pop)
% Function: pop = DetermineDomination(pop)
%
% Description: 计算个体之间的支配关系，若被其他个体支配，将 IsDominated 设置为 true
%
%
% Syntax:
%   
%
% Parameters:
%   pop：种群
%
% Return:
%   pop：进行非支配标记后的种群
%
%                  Young99
%         Revision:1.0     Data: 2022-12-07
%*************************************************************************

    nPop = numel(pop);
    
    % 初始化每个个体均为非支配个体
    for i = 1:nPop
        pop(i).IsDominated = false;
    end
    
    % 两两个体比较
    for i = 1:nPop-1
        for j = i+1:nPop
            
            if Dominates(pop(i), pop(j))
               pop(j).IsDominated = true;
            end
            
            if Dominates(pop(j), pop(i))
               pop(i).IsDominated = true;
            end
            
        end
    end

end

Dominates.m：两两个体之间比较大小

function b = Dominates(x, y)
% Function: b = Dominates(x, y)
%
% Description: 比较两个个体的函数值
%
%
% Syntax:
%   
%
% Parameters:
%   pop：种群
%
% Return:
%   b：比较结果，为布尔型
%
%                  Young99
%         Revision:1.0     Data: 2022-12-07
%*************************************************************************
    if isstruct(x)
        x = x.Cost;
    end
    
    if isstruct(y)
        y = y.Cost;
    end

    b = all(x <= y) && any(x

CreateGrid.m：创建自适应网格

function Grid = CreateGrid(pop, nGrid, alpha)
% Function: Grid = CreateGrid(pop, nGrid, alpha)
%
% Description: 为每一个目标函数，选出 pop 中个体目标函数值的最小及最大值
%              将最小最大值利用 alpha 参数扩展一定的范围，作为当前维度网格的上下限
%
%
% Syntax:
%   
%
% Parameters:
%   pop：rep 即为当前轮的非支配个体
%   nGrid：网格的维度大小
%   alpha：自定义参数，用于调整网格的最大最小上下线
%
% Return:
%   Grid：定义后的网格
%
%                  Young99
%         Revision:1.0     Data: 2022-12-07
%*************************************************************************

    c = [pop.Cost];
    
    cmin = min(c, [], 2);
    cmax = max(c, [], 2);
    
    dc = cmax-cmin;
    cmin = cmin-alpha*dc;
    cmax = cmax+alpha*dc;
    
    nObj = size(c, 1);
    
    empty_grid.LB = [];
    empty_grid.UB = [];
    Grid = repmat(empty_grid, nObj, 1);
    
    for j = 1:nObj
        
        cj = linspace(cmin(j), cmax(j), nGrid+1);
        
        Grid(j).LB = [-inf cj];
        Grid(j).UB = [cj +inf];
        
    end

end

FindGridIndex.m：为每个个体确定在网格中的位置

function particle = FindGridIndex(particle, Grid)
% Function: particle = FindGridIndex(particle, Grid)
%
% Description: 为 rep 中的每个个体划分所在的网格，其中 
%              GridSubIndex 表示每维目标所对应的网格位置
%              GridIndex 表示将 GridSubIndex 归并为一个数来表示
%
%
% Syntax:
%   
%
% Parameters:
%   particle：当前非支配集中的一个个体
%   Grid：已经划分好的网格，用于自适应网格算法
%
% Return:
%   particle：划分到对应网格后的个体
%
%                  Young99
%         Revision:1.0     Data: 2022-12-07
%*************************************************************************
    nObj = numel(particle.Cost);
    
    nGrid = numel(Grid(1).LB);
    
    particle.GridSubIndex = zeros(1, nObj);
    
    for j = 1:nObj
        
        particle.GridSubIndex(j) = ...
            find(particle.Cost(j)

SelectLeader.m：利用网格聚集密度选择 gBest

function leader = SelectLeader(rep, beta)
% Function: leader = SelectLeader(rep, beta)
%
% Description: 利用轮盘赌选出其中一个网格，网格聚集密度越小，越容易被选中，
%              再在选中的网格中随机选出一个个体作为 leader 即 gbest
%
%
% Syntax:
%   
%
% Parameters:
%   rep：当前迭代的非支配个体
%   beta：自定义参数
%
% Return:
%   leader：被选中的 gbest 
%
%                  Young99
%         Revision:1.0     Data: 2022-12-07
%*************************************************************************


    % Grid Index of All Repository Members
    GI = [rep.GridIndex];
    
    % Occupied Cells
    OC = unique(GI);
    
    % Number of Particles in Occupied Cells
    N = zeros(size(OC));
    for k = 1:numel(OC)
        N(k) = numel(find(GI == OC(k)));
    end
    
    % Selection Probabilities
    P = exp(-beta*N);  % 注意这是有负数，表示个体数越多的网格被选择的概率越小
    P = P/sum(P); % 转化为和为 1 的概率
    
    % Selected Cell Index
    sci = RouletteWheelSelection(P);
    
    % Selected Cell
    sc = OC(sci);
    
    % Selected Cell Members
    SCM = find(GI == sc);
    
    % Selected Member Index，random selection
    smi = randi([1 numel(SCM)]);
    
    % Selected Member
    sm = SCM(smi);
    
    % Leader
    leader = rep(sm);

end

RouletteWheelSelection.m： 轮盘赌

function i = RouletteWheelSelection(P)
% 轮盘赌用于选择某个网格
    r = rand;
    
    C = cumsum(P);
    
    i = find(r <= C, 1, 'first');

end

Mutation.m：变异操作

function particle = Mutation(particle, pm, VarMin, VarMax)
% Function: particle = Mutation(particle, pm, VarMin, VarMax)
%
% Description: 随机选择一个决策变量进行变异，避免陷入局部最优
%
%
% Syntax:
%   
%
% Parameters:
%   particle：个体决策变量
%   pm：扰乱算子
%   VarMin：变量最小值
%   VarMax：变量最大值
%
% Return:
%   particle：变异后的个体
%
%                  99Young99
%         Revision:1.0     Data: 2022-12-09
%*************************************************************************


    nVar = numel(particle);
    p = randi([1 nVar]); % 随机选取一个变异位置 p
    
    x = particle(p);

    d = pm * (VarMax - VarMin);
    ub = x + d; 
    lb = x - d;
    ub = min(ub, VarMax);
    lb = max(lb, VarMin);

    x = unifrnd(lb, ub, 1);

    particle(p) = x;

end

DeleteOneRepMemebr.m：当 rep 超出阈值，进行删除操作

function rep = DeleteOneRepMemebr(rep, gamma)
% Function: rep = DeleteOneRepMemebr(rep, gamma)
%
% Description: 利用轮盘赌选出其中一个网格，网格聚集密度越大，越容易被选中，
%              再在选中的网格中随机选出一个个体删除
%
%
% Syntax:
%   
%
% Parameters:
%   rep：当前迭代的非支配个体
%   beta：自定义参数
%
% Return:
%   leader：被选中的 gbest 
%
%                  Young99
%         Revision:1.0     Data: 2022-12-07
%*************************************************************************
    % Grid Index of All Repository Members
    GI = [rep.GridIndex];
    
    % Occupied Cells
    OC = unique(GI);
    
    % Number of Particles in Occupied Cells
    N = zeros(size(OC));
    for k = 1:numel(OC)
        N(k) = numel(find(GI == OC(k)));
    end
    
    % Selection Probabilities
    P = exp(gamma*N);
    P = P/sum(P);
    
    % Selected Cell Index
    sci = RouletteWheelSelection(P);
    
    % Selected Cell
    sc = OC(sci);
    
    % Selected Cell Members
    SCM = find(GI == sc);
    
    % Selected Member Index
    smi = randi([1 numel(SCM)]);
    
    % Selected Member
    sm = SCM(smi);
    
    % Delete Selected Member
    rep(sm) = [];

end

PlotCosts.m：画图可视化

function PlotCosts(pop, rep)

    pop_costs = [pop.Cost];
    plot(pop_costs(1, :), pop_costs(2, :), 'ko');
    hold on;
    
    rep_costs = [rep.Cost];
    plot(rep_costs(1, :), rep_costs(2, :), 'r*');
    
    xlabel('1^{st} Objective');
    ylabel('2^{nd} Objective');
    
    grid on;
    
    hold off;

end

HV.m

function [Score,PopObj] = HV(PopObj,PF)
%  
% Hypervolume

%------------------------------- Reference --------------------------------
% E. Zitzler and L. Thiele, Multiobjective evolutionary algorithms: A
% comparative case study and the strength Pareto approach, IEEE
% Transactions on Evolutionary Computation, 1999, 3(4): 257-271.
%------------------------------- Copyright --------------------------------
% Copyright (c) 2018-2019 BIMK Group. You are free to use the PlatEMO for
% research purposes. All publications which use this platform or any code
% in the platform should acknowledge the use of "PlatEMO" and reference "Ye
% Tian, Ran Cheng, Xingyi Zhang, and Yaochu Jin, PlatEMO: A MATLAB platform
% for evolutionary multi-objective optimization [educational forum], IEEE
% Computational Intelligence Magazine, 2017, 12(4): 73-87".
%--------------------------------------------------------------------------

% 
% 这段代码是用来计算超体积指标的。它包含了一个 HV 函数，用于计算超体积指标，并输出其值和输入种群的结果。
% 
% HV 函数的输入参数包括种群结果 PopObj 和理论最优结果 PF。它首先会将种群结果进行归一化，然后根据超体积指标的定义，计算种群结果与理论最优结果的相似度。
% 
% 最后，HV 函数会输出计算得到的超体积指标值和归一化后的种群结果。


    % Normalize the population according to the reference point set
    [N,M]  = size(PopObj);
    fmin   = min(min(PopObj,[],1),zeros(1,M));
    fmax   = max(PF,[],1);
    PopObj = (PopObj-repmat(fmin,N,1))./repmat((fmax-fmin)*1.1,N,1);
    PopObj(any(PopObj>1,2),:) = [];
    % The reference point is set to (1,1,...)
    RefPoint = ones(1,M);
    if isempty(PopObj)
        Score = 0;
    elseif M < 4
        % Calculate the exact HV value
        pl = sortrows(PopObj);
        S  = {1,pl};
        for k = 1 : M-1
            S_ = {};
            for i = 1 : size(S,1)
                Stemp = Slice(cell2mat(S(i,2)),k,RefPoint);
                for j = 1 : size(Stemp,1)
                    temp(1) = {cell2mat(Stemp(j,1))*cell2mat(S(i,1))};
                    temp(2) = Stemp(j,2);
                    S_      = Add(temp,S_);
                end
            end
            S = S_;
        end
        Score = 0;
        for i = 1 : size(S,1)
            p     = Head(cell2mat(S(i,2)));
            Score = Score + cell2mat(S(i,1))*abs(p(M)-RefPoint(M));
        end
    else
        % Estimate the HV value by Monte Carlo estimation
        SampleNum = 1000000;
        MaxValue  = RefPoint;
        MinValue  = min(PopObj,[],1);
        Samples   = unifrnd(repmat(MinValue,SampleNum,1),repmat(MaxValue,SampleNum,1));
        if gpuDeviceCount > 0
            % GPU acceleration
            Samples = gpuArray(single(Samples));
            PopObj  = gpuArray(single(PopObj));
        end
        for i = 1 : size(PopObj,1)
            drawnow();
            domi = true(size(Samples,1),1);
            m    = 1;
            while m <= M && any(domi)
                domi = domi & PopObj(i,m) <= Samples(:,m);
                m    = m + 1;
            end
            Samples(domi,:) = [];
        end
        Score = prod(MaxValue-MinValue)*(1-size(Samples,1)/SampleNum);
    end
end

function S = Slice(pl,k,RefPoint)
    p  = Head(pl);
    pl = Tail(pl);
    ql = [];
    S  = {};
    while ~isempty(pl)
        ql  = Insert(p,k+1,ql);
        p_  = Head(pl);
        cell_(1,1) = {abs(p(k)-p_(k))};
        cell_(1,2) = {ql};
        S   = Add(cell_,S);
        p   = p_;
        pl  = Tail(pl);
    end
    ql = Insert(p,k+1,ql);
    cell_(1,1) = {abs(p(k)-RefPoint(k))};
    cell_(1,2) = {ql};
    S  = Add(cell_,S);
end

function ql = Insert(p,k,pl)
    flag1 = 0;
    flag2 = 0;
    ql    = [];
    hp    = Head(pl);
    while ~isempty(pl) && hp(k) < p(k)
        ql = [ql;hp];
        pl = Tail(pl);
        hp = Head(pl);
    end
    ql = [ql;p];
    m  = length(p);
    while ~isempty(pl)
        q = Head(pl);
        for i = k : m
            if p(i) < q(i)
                flag1 = 1;
            else
                if p(i) > q(i)
                    flag2 = 1;
                end
            end
        end
        if ~(flag1 == 1 && flag2 == 0)
            ql = [ql;Head(pl)];
        end
        pl = Tail(pl);
    end  
end

function p = Head(pl)
    if isempty(pl)
        p = [];
    else
        p = pl(1,:);
    end
end

function ql = Tail(pl)
    if size(pl,1) < 2
        ql = [];
    else
        ql = pl(2:end,:);
    end
end

function S_ = Add(cell_,S)
    n = size(S,1);
    m = 0;
    for k = 1 : n
        if isequal(cell_(1,2),S(k,2))
            S(k,1) = {cell2mat(S(k,1))+cell2mat(cell_(1,1))};
            m = 1;
            break;
        end
    end
    if m == 0
        S(n+1,:) = cell_(1,:);
    end
    S_ = S;     
end

IGD.m

function Score = IGD(PopObj,PF)

% PopObej：算法求得的非支配解集
% PF：真实 Pareto 解集

%  
% Inverted generational distance

%------------------------------- Reference --------------------------------
% C. A. Coello Coello and N. C. Cortes, Solving multiobjective optimization
% problems using an artificial immune system, Genetic Programming and
% Evolvable Machines, 2005, 6(2): 163-190.
%------------------------------- Copyright --------------------------------
% Copyright (c) 2018-2019 BIMK Group. You are free to use the PlatEMO for
% research purposes. All publications which use this platform or any code
% in the platform should acknowledge the use of "PlatEMO" and reference "Ye
% Tian, Ran Cheng, Xingyi Zhang, and Yaochu Jin, PlatEMO: A MATLAB platform
% for evolutionary multi-objective optimization [educational forum], IEEE
% Computational Intelligence Magazine, 2017, 12(4): 73-87".
%--------------------------------------------------------------------------

    % 通过 pdist 计算 PF 与 PopObj 两两欧式距离，通过 min 取每一行的最小值作为列向量
    % 最后再取所有距离的平均值，越小说明分布性和收敛性越

    Distance = min(pdist2(PF,PopObj),[],2); 
    Score    = mean(Distance);
end

Reference

部分理论来源于网络，如有侵权请联系删除

小手手动起来，点个赞再走呗 ~