SAR ADC系列2：DFT离散傅里叶变换

目录

ADC动态性能仿真/测试平台

DFT：离散傅里叶分析

DFT的 Matlab 实现：

频谱泄露：

如何规避频谱泄露：

ADC性能分析：DFT

Cadence环境下的DFT分析实例：

Matlab环境下的DFT分析实例：

---

ADC动态性能仿真/测试平台

        作为一个线性系统，如果输入为单频信号，则ADC输出应该只含有相同频率的单频信号fin，非线性会导致K*fin(K=2/3.…)的频谱分量。DNL、INL都会引起频域的非线性。

动态性能指标：

• SNR：Signal to Noise Ratio
• SNDR：Signal to Noise+Distortion Ration
• ENOB：Effective Number of Bits
• DR：Dynamic Range
• SFDR：Spurious Free Dynamic Range
• HD：Harmonic Distortion
• THD：Total Harmonic Distortion

---

DFT：离散傅里叶分析

DFT：Discrete Fourier Transform离散傅里叶变换，用于分析ADC输出信号的频谱。

• 以 Ts=1/fs 为时间间隔对样本进行采样，取N个采样样本做DTF，得到N个离散频率。
• 频率分量K代表的频率是 K*fs/N 。
• DFT的频率精度：
         ■ 相邻频谱之间频率间隔为 fs/N  。时域间隔是 N/fs 。
         ■ 总的采样时间为 N*Ts = N/fs 。
• DFT 和 FFT 的关系：
         如果N=2^K，则用FFT是更有效的算法。

注意：这里的第一根谱线是fs=0（即DC的谱线） ，第二根才是 fs/N 。总共N个点，第个是0，第N个是 (N-1)/N。

相干采样，ADC输出频率要落在 K*fs/N 谱线上才能看到！

DFT的 Matlab 实现：

■ 一个周期采样10个点，信号周期数=10

clear;
N  = 100 ; % 取输入波的 100 个点做DFT
fs = 1000; % 采样频率是 1000 Hz
fx = 100 ; % 信号的频率是 100 Hz
%以 采样频率1000Hz 去采样 频率100Hz信号 的100个点，相当于一个周期采10个点，一共采样10个周期100个点

x = cos(2*pi*fx/fs*[0:N-1]); %输入信号
s = abs(fft(x));             %取幅值
plot(s, 'linewidth', 2);
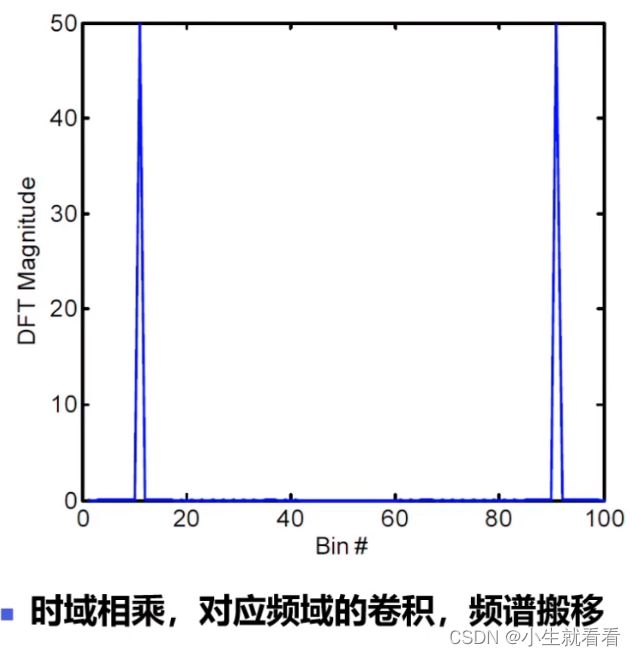
% 横坐标是点数，纵坐标是幅值

■ 对 x = cos(2*pi*fx/fs*[0:N-1]); 说明：
        2*pi*fx 是输入信号频率，在 K/fs 处采集一个点，K的取值为[0:N-1]
        （上文：以 Ts = 1/fs 为时间间隔进行采样）
信号有两根谱线：频谱混叠， 以 fs/2 为轴对称分布，实际只要看一半即可。

clear;
N  = 100;
fs = 1000;
fx = 100;
FS = 1; % full-scale amplitude--幅度为1

x = FS*cos(2*pi*fx/fs*[0:N-1]); % 2*pi*fx是输入信号频率，在 K/fs 处采集一个点，K为[0:N-1]
s = abs(fft(x));
% remove redundant half of spectrum
s = s(1:end/2);
% normalize magnitudes to dBFS
% dBFS = dB relative to full-scale
s = 20*log10(2*s/N/FS);
% frequency vector
f = [0:N/2-1]/N; % 取一半的频率

plot(f, s, 'LineWidth',2);
xlabel('Frequency [f/fs]')
ylabel('DFT Magnitude [dBFS]')
% 横坐标归一化f/fs，纵坐标幅值dB

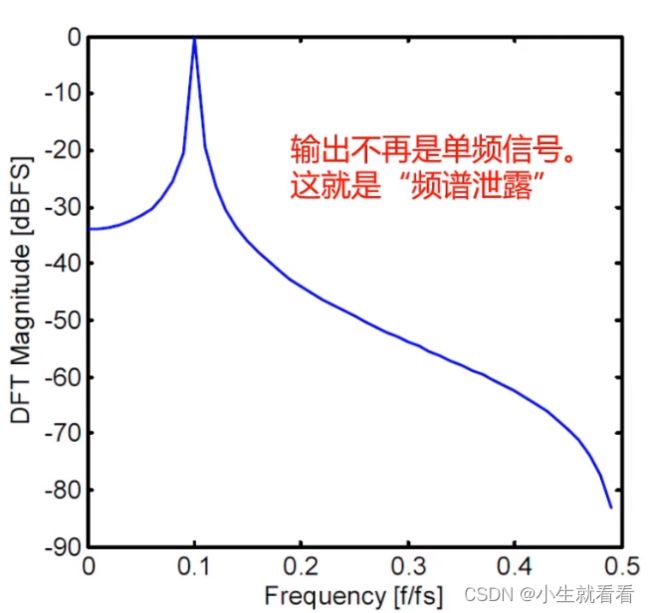
 ■ 频谱泄露：

将 fx = 100；改成 fx = 101；就会发生频谱泄露。谱线尖峰位置为 101/1000。

• 通常人脑会按照左下图的红色部分拓展sin波，且主观认为它是一个周期信号
• 对DFT，情况就不一样了！机器无法判断它得到的信号到底是1个完整的信号周期，还是2个，或者是2.3个。机器的脑补操作，就是把采样到的信号当成一个完整的周期，然后按照右下图那样去拓展。就会出现频谱泄露！

 所以一定要 采样整数个周期给DFT。

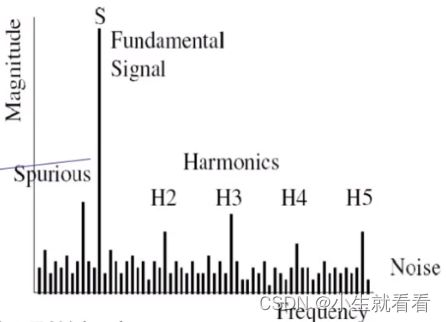
• 从傅里叶级数可知，任何一个周期信号，都可以用它的基波和谐波加权来表示。
• 对于DFT而言，fs 的采样率，采了N个点的信号，总共花费了N/fs秒，意味着基波频率就是 fs/N，DFT会将这 N/fs 秒进行周期性延拓。任何信号都可以用频率为 fs/N 的基波以及它的谐波加权构成。换言之，DFT输出频谱只会出现一系列的离散频谱，这些离散频谱频率为0、fs/N、2fs/N、 ……(N-1)*fs/N 。 
• 如果输入信号频率fin不满足 fin=K*fs/N，则输入信号不会落在任何一根谱线上，此时输入信号的能量会分摊到好几根谱线上，我们称这种现象为出现频谱泄露

如何规避频谱泄露：

        方法一：保证送给DFT的信号是整数个周期（相干采样）：M/N = fin/fs 即：fin = fs / N *M——（fin 为频率 fs/N 的整数倍）
      （其中：M为信号周期数，N为DFT的点数，fin为输入信号频率，fs为采样频率）
        方法二：给信号加窗（Window）

---

ADC性能分析：DFT

DFT对采用频率的要求：满足采样定理，fs > 2*fin_max

相干采样：
                                          
        上式中M为信号周期数，N为DFT采样点数，fin为信号频率，fs为采样频率。M取奇数，N取2^K，如1024、4096。（让M/N不能约分，才能充分利用所有的点）
        即 fin 为 M倍的 fs/N （基波频率的M倍）。是第 (M+1) 个点 (第一个点是DC)。

---

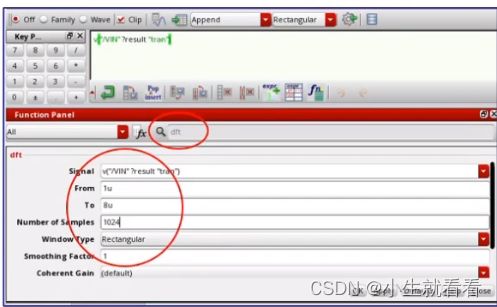
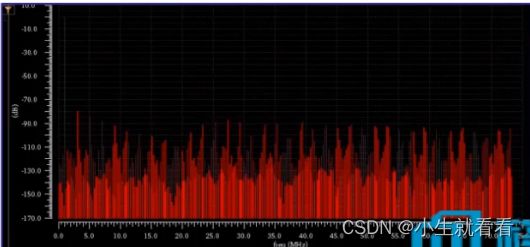
Cadence环境下的DFT分析实例：

目标：在Cadence环境下对一个连续时间信号 A=sin(2*pi*1e6*t) 进行频谱分析----1MHz正弦波

方法：利用Cadence Calculator自带函数 dft( ) 完成
        ■ 截取一段整数个周期的信号波形，在此 1us~8us，共 7us，对应M=7
        ■ 取采点数N=1024,通过相干采样公式可以计算 fs=N*fin/M
        ■ 将dft结果取dB20(）

---

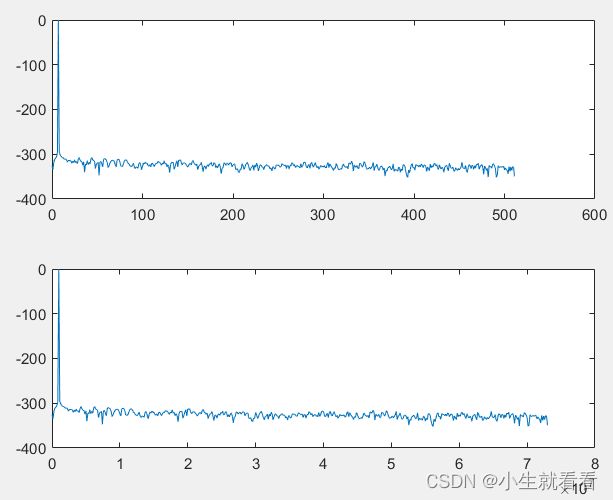
Matlab环境下的DFT分析实例：

 同上，1MHz正弦波，N=1024，M=7。

clear; clc;
N = 1024;
M = 7;
fin = 1e6;  % 输入信号频率1MHz

fs = N*fin/M; % 通过公式计算出采样频率fs
Ts = 1/fs;
t = 0:Ts:(N-1)*Ts; % 采样时域点数，以Ts步进
vin = sin(2*pi*fin*t); % 采样后的正弦波
figure(1);
plot(t,vin)

s = fft(vin); % FFT分析
s = abs(s);   % 取模 
s = 20*log10(s); % 换算dB
% normalize magnitudes to fin tone
s = s - max(s); % 幅度归一化
% remove redundant half of spectrum
s = s(1:N/2); % 取频谱一半

figure(2);
subplot(2,1,1);
plot(0:N/2-1,s); % 点数0~N/2-1

subplot(2,1,2);
f = (0:N/2-1)*fs/N; % 频率归一化
plot(f,s);