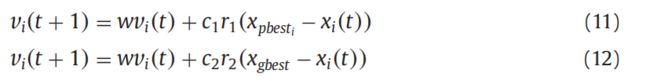一种具有多搜索策略的多目标粒子群算法（MMOPSO）

1.摘要

大多数的MOPSO算法只采用单一的搜索策略来更新每个粒子的速度（单目标优化问题（SOP）），这可能会给复杂的MOPSO算法带来一定的困难。提出了一种基于MMOPSO算法的MOPSO算法，利用分解方法将MOPS转换为一组聚合问题，然后相应地分配粒子来优化每个聚集问题。设计了两种搜索策略来更新每个粒子的速度，这分别有利于加快收敛速度和保持种群多样性。在此之后，粒子访问的所有非主导解决方案都保存在外部存档中，其中，进一步执行进化搜索策略以在它们之间交换有用的信息。

2.介绍

一般情况下，现有的MOPSO算法可分为两类。第一类将Pareto优势关系嵌入粒子群算法，用于确定个体最佳状态和全球最佳粒子。第二种算法采用分解方法，利用传统的粒子群算法可以直接解决MOPS。但是，在处理复杂的MOPS问题时，大多数MOPSO算法都不能有效地逼近真正的PF。因此，本文提出了一种新的多搜索策略的MOPSO算法MMOPSO。设计了两种更新粒子速度的搜索策略，分别加快了收敛速度和保持了种群多样性。为了让精英信息在外部档案中共享，进行了一个由模拟二进制交叉（SBX）和多项式突变（PM）组成的进化搜索策略，该策略增强了MMOPOS的探索能力。与现有的MOPSO算法相比，MMOPSO算法的新颖性可以概括为以下几个方面：

1）与大多数MOPSO算法中采用的单一搜索模式不同，MMOPSO算法设计了两种搜索策略来更新每个粒子的速度，其目的是分别加速收敛速度和保持种群多样性。他们的实行是由一个预先确定的界限来决定的，以保持开采和勘探的平衡。

2）在PSO的外部存档上运行进化搜索策略，从而有利于精英个体间的信息交流。进化算子可以为粒子群算法提供另一种搜索能力，弥补基于粒子群算法的搜索在处理一些困难的搜索时的不足。

3）在MMOPSO中给出了个人最佳粒子和全局最优粒子的新定义。传统上，个人最佳粒子和全球最佳粒子分别是每个粒子和群体中的粒子所寻找到的最佳粒子。然而，在MMOPSO中，采用分解方法将MOP转换成一组SOPs。个人最佳粒子和全局最佳粒子分别被认为是每个聚合问题和所有SOPs的最佳值。因此，MMOPSO可以通过使用PSO搜索来优化每个聚集问题。

3.相关工作

3.1Pareto相关定义

3.2分解

在一定的条件下，最优解可以是一个以集合为目标的标量优化问题的最优解。因此，发现的PF可以分解为一组SOP。常用方法有加权和、切比雪夫和边界交点法。在MMOPSO中采用了边界相交法（PBI）。

通过上述MOPSO算法的启发，提出的MMOPSO算法还将MOPS分解为一组聚合问题，并采用拥挤归档文件保存多个非支配的解。然而，与上述的MOPSO算法相比，MMOPSO的不同特点包括两种旨在更新每个粒子的速度的搜索策略，即进化搜索。在档案中执行的战略，在精英个人之间交换有益的信息，这是个人最佳和全球最佳粒子的新定义。所有这些新特性在收敛速度和群多样性方面都提高了MMOPSO算法的收敛速度，并在实验研究中进行了分析和讨论。

3.3PSO

其中t是迭代次数，w是惯性权重，c1和c2分别是个人最佳粒子和全局最优粒子的两个学习因子，r1和r2是两个随机数。

4.MMOPSO

所提出的MMOPSO算法是基于分解方法将MOP变换成一组标量聚集问题，采用边界交点法。MMOPSO中的每个粒子通过更新其飞行速度来优化每个聚集问题，然后将粒子访问的所有非支配解保持在一个有限大小档案外部中。一旦存档文件满了，具有更大拥挤距离值的非主导解决方案将被保留。在下面的小节中，介绍了MMOPSO的主要步骤，如两种搜索策略。对于速度更新，分别描述了外部存档和归档更新的进化搜索。最后给出了完整的MMOPSO算法。

4.1速度更新的两种搜索策略

在传统粒子群算法中，粒子的速度和位置值通常根据个人最佳粒子和全局最优粒子的位置信息进行更新。在MMOPSO中引入了两个速度更新方程，分别用于搜索空间的开发和探索。它们与分解方法相配合，试图对每个聚合问题进行优化。假设群中存在N个粒子，对于每个粒子i(i=1,2,...,N)，它与边界相交法中使用的唯一权重向量λ相关联。在MMOPSO中，粒子I(i=1，2，.，N)的速度按下面展示：

其中t是迭代次数，w是惯性权重，C1和c2是两个学习因子，r1和r2是[0，1]中两个均匀分布的随机数。值得注意的是xpbesti从外部存档 A = { A 1 ，A 2 ，... ，A |A|} 之间的解中选择，，它给出了与权向量λi对应的每个聚集问题的最佳值。下图是选择伪代码：

另一方面，由于外部存档A中的解决方案都是非支配的，因此可以认为它们是MOPS的全局最佳值。因此，从外部存档A中随机选择xgest。因此，当使用公式11去更新速度，它将迅速引导相应的粒子接近最优聚集值附近的邻近区域，从而增强了开发和结果的能力，加速收敛速度。否则，用公式12，它将引导目标粒子搜索xgbest和它自己之间的中间区域。这对于提高勘探和同时改善群多样性是有益的。因此，MMOPSO通过使用预定义的阈值δ来组合两个搜索模式,如下所述:

4.2 存档的进化搜索

在基于PSO的优化之后，在外部存档A中保留了具有更大的拥挤距离值的被访问的非支配性解决方案，这些方案被认为是整个PF的良好解。为了允许存档之间的有益信息交换，MMOPSO对存档中的每个非支配的解决方案执行进化搜索。嵌入式进化搜索能力可以修复 PSO 搜索的潜在漏洞。这得到了近年来进化算法研究的支持，即杂交搜索能力可以提高搜索能力和鲁棒性，以解决各种 MOPs 。在MMOPSO算法中，在多目标优化算法中广泛采用了模拟二进制交叉(SBX)和多项式突变(PM)等进化算子。

SBX算子允许精英解决方案交换有用的基因片段，而PM操作则注入一个小的湍流来搜索局部区域。在外部存档上执行SBX和PM操作符首先从A中选取了一个精英子集E，其中包含了A中具有较大拥挤距离值的一些非支配解。E的大小一般比A小，并且在本文中被设为A的一半。对于每一个解AI(i=1，2，.，x_A_x)，在[1，|E|]中生成一个随机整数j。然后，使用Ai和Ej作为执行SBX操作符的父解决方案。SBX操作符中的一个子解决方案是随机选择的，然后进一步执行PM操作符。伪代码如下：

其中SBX(Ai，Ej)是指在父解决方案Ai和Ej上执行SBX操作符，C1和C2是由SBX操作员生成的子解决方案，PM(CK)指示PM操作员在CK上的执行。之后，生成一个新的解决方案集S。加入到存档中去。

4.3存档更新

在执行PSO搜索或进化搜索后，将生成的新的非主导解决方案收集到外部存档中。由于存档的大小是有限的，而非支配性解决方案的数量可能是无限的，因此必须使用适当的选择机制进行归档更新，这有助于引导搜索方向走向真正的pf。假设新生成的解决方案集为S，外部存档中的解决方案集为A，则归档更新过程的伪代码如下：

CheckDominance(x，y)返回解X和Y之间的Pareto优势关系。如果函数返回1，则表示x主导y。否则，函数返回-1。Y支配或等于X。另一个函数CrowdingDistingAssignment(A)将计算每个解决方案在A中的拥挤距离值。

4.4整合

在初始化阶段，首先初始化 N 个权重向量，然后随机生成带有 N 个粒子的群，其中每个粒子与一个唯一的权重向量相关联。外部存档文件A被初始化为空。评估每个粒子的目标后，执行归档更新程序，以保存存档A中的非主导解决方案。然后，MMOPSO变成进化过程的循环，直到函数评估时间ev达到预定的最大时间max_ev为止。在算法的最后，将存档A中的非占优解作为最后的近似PF。

5.结论

文章提出了一种新的基于分解方法的多搜索策略的MOPSO算法，将MOPS转换为一组聚合问题。相应地，群中的每个粒子被分配到优化每个聚集问题。设计了一种新的速度更新方法，利用两种搜索策略对粒子速度进行更新，既提高了收敛速度，又保持了种群多样性。此外，进化搜索策略在外部存档中的非支配解决方案上进一步执行，该解决方案能够交换它们的有益信息。这种嵌入的进化搜索能力可以修复PSO搜索模式的弱点，从而大大提高了MMOPSO求解各种MOPS的综合性能。