第三章 word2vec
目录
- 3.1 基于推理的方法和神经网络
-
- 3.1.1 基于计数的方法的问题
- 3.1.2 基于推理的方法的概要
- 3.1.3 神经网络中单词的处理方法
- 3.2 简单的 word2vec
-
- 3.2.1 CBOW模型的推理
- 3.2.2 CBOW模型的学习
- 3.2.3 word2vec的权重和分布式表示
- 3.3 学习数据的准备
-
- 3.3.1 上下文和目标词
- 3.3.2 转化为one-hot表示
- 3.4 CBOW模型的实现
- 3.5 word2vec的补充说明
-
- 3.5.1 CBOW模型和概率
- 3.5.2 skip-gram模型
- 3.5.3 基于计数与基于推理
3.1 基于推理的方法和神经网络
用向量表示单词的方法大致分为两种:
- 基于计数的方法
- 基于推理的方法
虽然两者在获得单词含义的方法上差别很大,但是两者的背景都是分布式假设。
3.1.1 基于计数的方法的问题
基于计数的方法根据一个单词周围的单词的出现频数来表示该单词。具体来说,先生成所有单词的共现矩阵,再对这个矩阵进行 SVD,以获得密集向量(单词的分布式表示)。但是,基于计数的方法在处理大规模语料库时会出现问题。
在现实世界中,语料库处理的单词数量非常大。比如,据说英文的词汇量超过 100 万个。如果词汇量超过 100 万个,那么使用基于计数的方法就需要生成一个 100 万 × 100 万的庞大矩阵,但对如此庞大的矩阵执行 SVD 显然是不现实的。
注意,对于 n × n n\ \times \ n n × n 的矩阵,SVD 的复杂度为 O ( n 3 ) O(n^3) O(n3)。
基于计数的方法使用整个语料库的统计数据(共现矩阵和 PPMI 等), 通过一次处理(SVD 等)获得单词的分布式表示。而基于推理的方法使用神经网络,通常在 mini-batch 数据上进行学习。这意味着神经网络一次只需要看一部分学习数据(mini-batch),并反复更新权重。
基于计数的方法一次性处理全部学习数据;反之,基于推理的方法使用部分学习数据逐步学习。这意味着,在词汇量很大的语料库中,即使 SVD 等的计算量太大导致计算机难以处理,神经网络也可以在部分数据上学习。并且,神经网络的学习可以使用多台机器、多个 GPU 并行执行,从而加速整个学习过程。在这方面,基于推理的方法更有优势。
3.1.2 基于推理的方法的概要
基于推理的方法的主要操作是“推理”。如图 3-2 所示,当给出周围的 单词(上下文)时,预测 “?” 处会出现什么单词,这就是推理。
解开图 3-2 中的推理问题并学习规律,就是基于推理的方法的主要任务。通过反复求解这些推理问题,可以学习到单词的出现模式。从“模型视角”出发,这个推理问题如图 3-3 所示。
如图 3-3 所示,基于推理的方法引入了某种模型,这里将神经网络用于此模型。这个模型接收上下文信息作为输入,并输出(可能出现的)各个单词的出现概率。在这样的框架中,使用语料库来学习模型,使之能做出正确的预测。另外,作为模型学习的产物,我们得到了单词的分布式表示。这就是基于推理的方法的全貌。
基于推理的方法和基于计数的方法一样,也基于分布式假设。分布式假设假设“单词含义由其周围的单词构成”。基于推理的方法将这一假设归结为了上面的预测问题。由此可见,不管是哪种方法,如何对基于分布式假设的“单词共现”建模都是最重要的研究主题。
3.1.3 神经网络中单词的处理方法
神经网络无法直接处理 you 或 say 这样的单词,要用神经网络处理单词,需要先将单词转化为固定长度的向量。对此,一种方式是将单词转换为one-hot表示(one-hot 向量)。在 one-hot 表示中,只有一个元素是 1,其他元素都是 0。
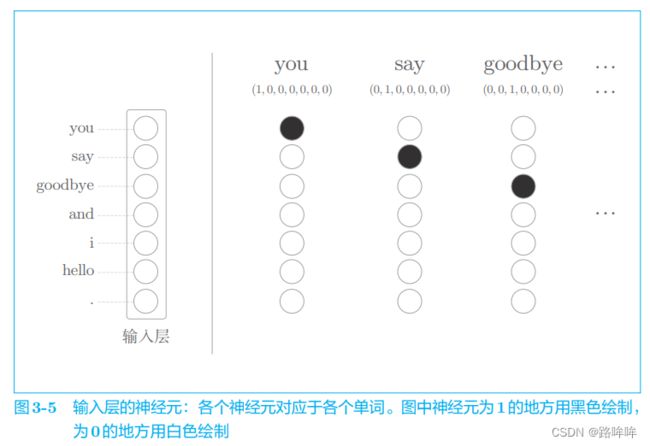
一个 one-hot 表示的例子。用 You say goodbye and I say hello. 这个一句话的语料库来说明,在这个语料库中, 一共有 7 个单词(“you”“say”“goodbye”“and”“i”“hello”“.”)。此时, 各个单词可以转化为图 3-4 所示的 one-hot 表示。
只要将单词转化为固定长度的向量,神经网络的输入层的神经元个数就可以固定下来,如图3-5
如图 3-5 所示,输入层由 7 个神经元表示,分别对应于 7 个单词(第 1 个神经元对应于 you,第 2 个神经元对应于 say)。
只要将单词表示为向量,这些向量就可以由构成神经网络的各种 “层” 来处理。比如,对于one-hot表示的某个单词, 使用全连接层对其进行变换的情况如图 3-6 所示。
如图 3-6 所示,全连接层通过箭头连接所有节点。这些箭头拥有权重(参数),它们和输入层神经元的加权和成为中间层的神经元。
在图 3-6 中,神经元之间的连接是用箭头表示的。之后,为了明确地显 示权重,我们将使用图 3-7 所示的方法。
对于全连接层的代码表示如下 :
c = np.array([[1, 0, 0, 0, 0, 0, 0]]) # 输入
W = np.random.randn(7, 3) # 权重
h = np.dot(c, W) # 中间节点
print(h)
# [[-0.70012195 0.25204755 -0.79774592]]
这段代码将单词 ID 为 0 的单词表示为了 one-hot 表示,并用全连接层对其进行了变换。
这里要体会 c × W c \ \times \ W c × W 的含义:因为 c c c 是使用 one-hot 表示的一个单词,单词 ID 对应的元素是 1,其它地方都是 0。因此式子 c × W c \ \times \ W c × W 的作用就相当于从矩阵 W W W 中提取出权重对应的某一行。
比如下面式子为例:
[ 0 1 0 ] [ 1 1 1 2 2 2 3 3 3 ] = [ 2 2 2 ] \begin{bmatrix} 0 &1 &0 \end{bmatrix} \begin{bmatrix} 1 &1 &1 \\ 2 &2 &2 \\ 3 &3 &3 \\ \end{bmatrix}= \begin{bmatrix} 2 &2 &2 \end{bmatrix} [010] 123123123 =[222]

3.2 简单的 word2vec
这里使用由原版 word2vec 提出的名为 continuous bag-of-words(CBOW)的模型作为神经网络。
CBOW 模型 和 skip-gram 模型都是 word2vec 中使用的两个神经网络。
3.2.1 CBOW模型的推理
下面讨论的 CBOW 模型基本上是一个 2 层的神经网络,结构非常简单。
CBOW 模型是根据上下文预测目标词的神经网络(“目标词”是指中间 的单词,它周围的单词是“上下文”)。通过训练这个 CBOW 模型,使其能尽可能地进行正确的预测,我们可以获得单词的分布式表示。
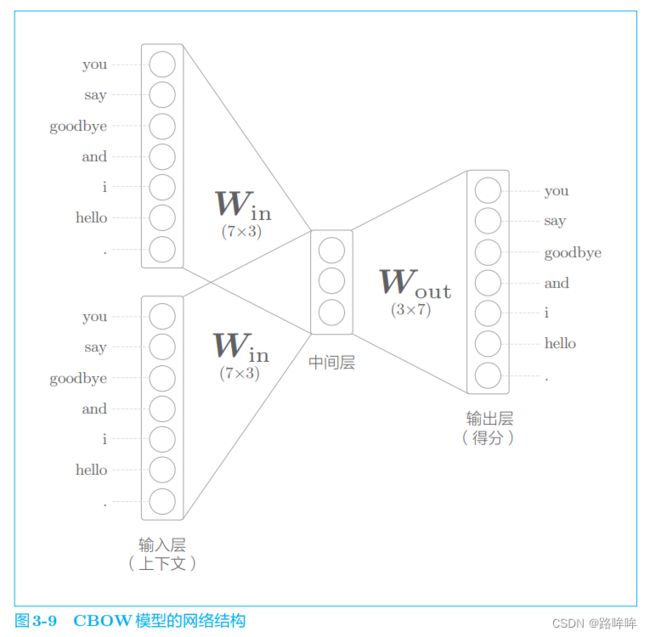
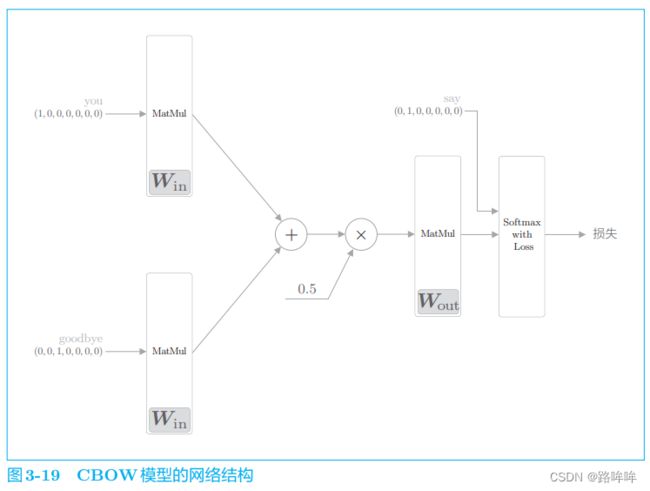
CBOW 模型的输入是上下文。这个上下文用 ['you', 'goodbye'] 这样的单词列表表示。我们将其转换为 one-hot 表示,以便 CBOW 模型可以进行处理。其模型如下图所示:
图 3-9 是 CBOW 模型的网络。它有两个输入层,经过中间层到达输出层。这里,从输入层到中间层的变换由相同的全连接层(即共享权重,权重为 W i n W_{in} Win)完成, 从中间层到输出层神经元的变换由另一个全连接层(权重为 W o u t W_{out} Wout)完成。
对于中间层的神经元是各个输入层经全连接层变换后得到的值的“平均”。
这里输出层有 7 个神经元,这些神经元对应于各个单词。输出层的神经元是各个单词的得分,它的值越大,说明对应单词的出现概率就越高。得分是指在被解释为概率之前的值, 对这些得分应用 Softmax 函数,就可以得到概率。
因为对上下文仅考虑两个单词,所以输入层有两个。 如果对上下文考虑 N 个单词,则输入层会有 N 个。
如图 3-9 所示,从输入层到中间层的变换由全连接层(权重是 W i n W_{in} Win)完成。此时,全连接层的权重 W i n W_{in} Win 是一个 7 × 3 的矩阵,这个权重就是我们要的单词的分布式表示,如图 3-10 所示。
如图 3-10 所示,权重 W i n W_{in} Win 的各行保存着各个单词的分布式表示。通过反复学习,不断更新各个单词的分布式表示,以正确地从上下文预测出应当出现的单词。令人惊讶的是,如此获得的向量很好地对单词含义进行了编码。这就是 word2vec 的全貌。
中间层的神经元数量比输入层少这一点很重要。中间层需要将预测单词所需的信息压缩保存,从而产生密集的向量表示。
到目前为止,我们从神经元视角图示了 CBOW 模型。下面,我们从层视角图示 CBOW 模型。这样一来,这个神经网络的结构如图 3-11 所示。
这里我们见到的 CBOW 模型是没有使用激活函数的简单的网络结构。除了多个输入层共享权重外,并没有什么难点。
3.2.2 CBOW模型的学习
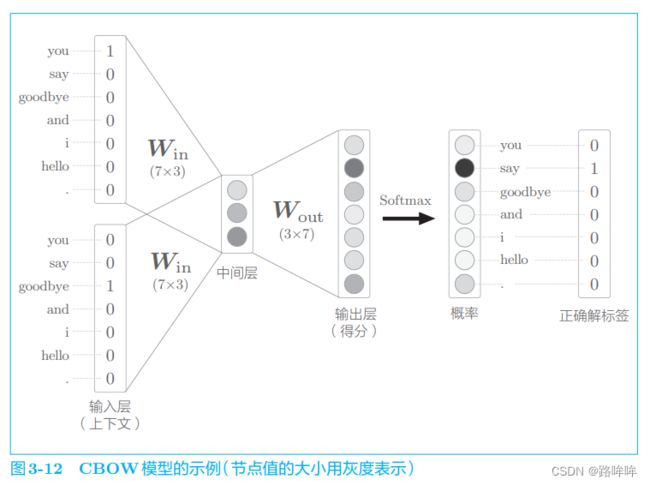
CBOW模型会在输出层输出了各个单词的得分, 通过对这些得分应用 Softmax 函数,可以获得概率(图 3-12)。这个概率表示哪个单词会出现在给定的上下文(周围单词)中间。
在图 3-12 所示的例子中,上下文是 you 和 goodbye,正确解标签(神经网络应该预测出的单词)是 say。这时,如果网络具有“良好的权重”, 那么在表示概率的神经元中,对应正确解的神经元的得分应该更高。
CBOW 模型的学习就是调整权重,以使预测准确。其结果是,权重 W i n W_{in} Win(确切地说是 W i n W_{in} Win 和 W o u t W_{out} Wout 两者)学习到蕴含单词出现模式的向量。根据过去的实验,CBOW 模型(和 skip-gram 模型)得到的单词的分布式表 示,特别是使用维基百科等大规模语料库学习到的单词的分布式表示,在单词的含义和语法上符合我们直觉的案例有很多。
CBOW模型只是学习语料库中单词的出现模式。如果语料库不一样, 学习到的单词的分布式表示也不一样。
3.2.3 word2vec的权重和分布式表示
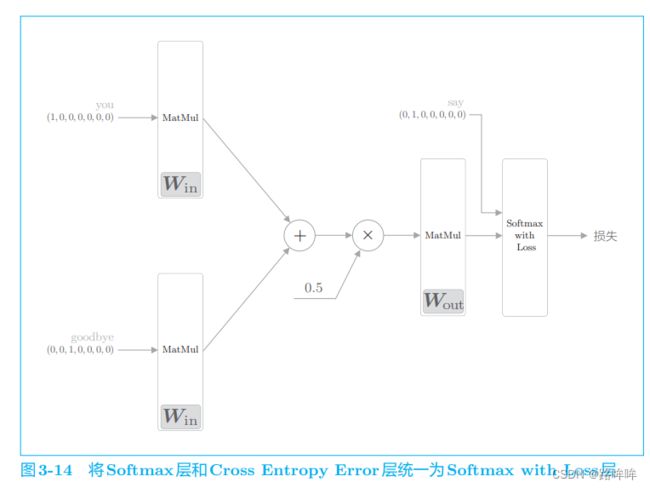
如前所述,word2vec 中使用的网络有两个权重,分别是输入侧的全连接层的权重( W i n W_{in} Win)和输出侧的全连接层的权重( W o u t W_{out} Wout)。一般而言,输入侧的权重 W i n W_{in} Win 的每一行对应于各个单词的分布式表示。另外,输出侧的权重 W o u t W_{out} Wout 也同样保存了对单词含义进行了编码的向量。只是,如图 3-15 所 示,输出侧的权重在列方向上保存了各个单词的分布式表示。
选择哪一个权重作为单词的分布式表示呢?有三种方案:
- 只使用输入侧的权重
- 只使用输出侧的权重
- 同时使用两个权重
前两个方案只使用其中一个权重。而在采用最后一个方案的情况下,根据如何组合这两个权重,存在多种方式,其中一个方式就是简单地将这两个权重相加。
就 word2vec(特别是 skip-gram 模型)而言,最受欢迎的是方案一。 许多研究中也都仅使用输入侧的权重 W i n W_{in} Win 作为最终的单词的分布式表示。 遵循这一思路,我们也使用 W i n W_{in} Win 作为单词的分布式表示。
3.3 学习数据的准备
在开始 word2vec 的学习之前,我们先来准备学习用的数据。这里我们仍以 You say goodbye and I say hello. 这个只有一句话的语料库为例进行说明。
3.3.1 上下文和目标词
word2vec 中使用的神经网络的输入是上下文,它的正确解标签是被这些上下文包围在中间的单词,即目标词。也就是说,我们要做的事情是,当向神经网络输入上下文时,使目标词出现的概率高(为了达成这一目标而进行学习)。
实现从语料库生成上下文和目标词的函数:
def create_contexts_target(corpus, window_size=1):
target = corpus[window_size:-window_size]
contexts = []
for idx in range(window_size, len(corpus)-window_size):
cs = []
for t in range(-window_size, window_size + 1):
if t == 0:
continue
cs.append(corpus[idx + t])
contexts.append(cs)
return np.array(contexts), np.array(target)
这个函数有两个参数:一个是单词 ID 列表(corpus);另一个是上下文的窗口大小(window_size)。
下面举一个例子:
import sys
sys.path.append('..')
from common.util import preprocess
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text) # 将语料库的文本转化成单词ID
print(corpus)
# [0 1 2 3 4 1 5 6]
print(id_to_word)
# {0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6: '.'}
contexts, target = create_contexts_target(corpus, window_size=1)
print(contexts)
# [[0 2]
# [1 3]
# [2 4]
# [3 1]
# [4 5]
# [1 6]]
print(target)
# [1 2 3 4 1 5
3.3.2 转化为one-hot表示
如图 3-18 所示,上下文和目标词从单词 ID 转化为了 one-hot 表示。 这里需要注意各个多维数组的形状。在上面的例子中,使用单词 ID 时的 contexts 的形状是 (6,2),将其转化为 one-hot 表示后,形状变为 (6,2,7)。
代码见书。
3.4 CBOW模型的实现
具体实现见书。
3.5 word2vec的补充说明
3.5.1 CBOW模型和概率
先说明概率表示:
-
概率记为 P ( ⋅ ) P(·) P(⋅),表示事件发生的概率;
-
联合概率记为 P ( A , B ) P(A, \ B) P(A, B),表示事件 A 和事件 B 同时发生的概率;
-
后验(条件)概率记为 P ( A ∣ B ) P(A\ |\ B) P(A ∣ B),字面意思是“事件发生后的概率”。从另一个 角度来看,也可以解释为“在给定事件 B(的信息)时事件 A 发生的概率”。
下面,我们用概率的表示方法来描述 CBOW 模型。CBOW 模型进行的处理是,当给定某个上下文时,输出目标词的概率。这里,我们使用包含单词 w 1 , w 2 , … , w T w_1,w_2, \dots,w_{T} w1,w2,…,wT 的语料库。如图 3-22 所示,对第 t 个单词,考虑窗口大 小为 1 的上下文。
下面,我们用数学式来表示当给定上下文 w t − 1 w_{t-1} wt−1 和 w t + 1 w_{t+1} wt+1 时目标词为 w t w_t wt 的概率。使用后验概率,下式:
P ( w t ∣ w t − 1 , w t + 1 ) P(w_t | w_{t-1}, w_{t+1}) P(wt∣wt−1,wt+1)
表示“在 w t − 1 w_{t-1} wt−1 和 w t + 1 w_{t+1} wt+1 发生后, w t w_t wt 发生的概率”,也可以解释 为“当给定 w t − 1 w_{t-1} wt−1 和 w t + 1 w_{t+1} wt+1 时, w t w_t wt 发生的概率”。
这里,使用上式可以简洁地表示 CBOW 模型的损失函数。这里将交叉熵误差函数套用在这里,交叉熵误差函数为:
L = − ∑ k t k l o g y k L = - \sum_kt_klog_{y_k} L=−k∑tklogyk
其中, y k y_k yk 表示第 k 个事件发生的概率。 t k t_k tk 是监督标签, 它是 one-hot 向量的元素。
这里需要注意的是,“ w t w_t wt 发生”这一事件是正确 解,它对应的 one-hot 向量的元素是 1,其他元素都是 0(也就是说,当 w t w_t wt 之外的事件发生时,对应的 one-hot 向量的元素均为 0)。考虑到这一点,可以推导出下式:
L = − l o g P ( w t ∣ w t − 1 , w t + 1 ) L = -logP(w_t|w_{t-1}, w_{t+1}) L=−logP(wt∣wt−1,wt+1)
上式为 CBOW 模型的损失函数,它只是对后验概率公式的概率取 log,并加上负号。顺便提一下,这也称为负对数似然(negative log likelihood)。上式是一 笔样本数据的损失函数。如果将其扩展到整个语料库,则损失函数可以写为:
L = − 1 T ∑ t = 1 T l o g P ( w t ∣ w t − 1 , w t + 1 ) L = -\frac{1}{T} \sum_{t=1}^T log P(w_t|w_{t-1}, w_{t+1}) L=−T1t=1∑TlogP(wt∣wt−1,wt+1)
CBOW 模型学习的任务就是让上式表示的损失函数尽可能地小。那时的权重参数就是我们想要的单词的分布式表示。这里,我们只考虑了窗口大小为 1 的情况,不过其他的窗口大小(或者窗口大小为 m 的一般情况) 也很容易用数学式表示。
3.5.2 skip-gram模型
skip-gram 是反转了 CBOW 模型处理的上下文和目标词的模型。
插入图3-23
如图所示,CBOW 模型从上下文的多个单词预测中间的单词(目标词),而 skip-gram 模型则从中间的单词(目标词)预测周围的多个单词 (上下文)。此时,skip-gram 模型的网络结构如下图所示:
插入图3-24
由图上图可知,skip-gram 模型的输入层只有一个,输出层的数量则与上下文的单词个数相等。因此,首先要分别求出各个输出层的损失(通过 Softmax with Loss 层等),然后将它们加起来作为最后的损失。
下面,使用概率的表示方法来表示 skip-gram 模型。我们来考虑根据中间单词(目标词) w t w_t wt 预测上下文 w t − 1 w_{t-1} wt−1 和 w t + 1 w_{t+1} wt+1 的情况。此时,skipgram 可以建模为下面的后验概率公式:
P ( w t − 1 , w t + 1 ∣ w t ) P(w_{t-1}, w_{t+1}|w_t) P(wt−1,wt+1∣wt)
上式表示“当给定 w t w_t wt 时, w t − 1 w_{t-1} wt−1 和 w t + 1 w_{t+1} wt+1 同时发生的概率”。这里,在 skip-gram 模型中,假定上下文的单词之间没有相关性(正确地说是假定 “条件独立”),将上式如下进行分解:
P ( w t − 1 , w t + 1 ∣ w t ) = P ( w t − 1 ∣ w t ) P ( w t + 1 ∣ w t ) P(w_{t-1}, w_{t+1}|w_t) = P(w_{t-1}|w_t)P(w_{t+1}|w_t) P(wt−1,wt+1∣wt)=P(wt−1∣wt)P(wt+1∣wt)
将上式代入交叉熵误差函数,可以推导出 skip-gram 模型的损失函数:
L = − l o g P ( w t − 1 , w t + 1 ∣ w t ) = − l o g P ( w t − 1 ∣ w t ) P ( w t + 1 ∣ w t ) = − ( l o g P ( w t − 1 ∣ w t ) + l o g P ( w t + 1 ∣ w t ) ) \begin{align*} L &= -log P(w_{t-1}, w_{t+1}|w_t) \\ &= -log P(w_{t-1}|w_t)P(w_{t+1}|w_t) \\ &= -(log P(w_{t-1}|w_t) + log P(w_{t+1}|w_t)) \end{align*} L=−logP(wt−1,wt+1∣wt)=−logP(wt−1∣wt)P(wt+1∣wt)=−(logP(wt−1∣wt)+logP(wt+1∣wt))
如上式,skipgram 模型的损失函数先分别求出各个上下文对应的损失,然后将它们加在 一起。式 (3.6) 是一笔样本数据的损失函数。如果扩展到整个语料库,则 skip-gram 模型的损失函数可以表示为下式:
L = − 1 T ∑ t = 1 T ( l o g P ( w t − 1 ∣ w t ) + l o g P ( w t + 1 ∣ w t ) ) L = -\frac{1}{T} \sum_{t=1}^{T}(log P(w_{t-1}|w_t) + log P(w_{t+1}|w_t)) L=−T1t=1∑T(logP(wt−1∣wt)+logP(wt+1∣wt))
比较 CBOW 和 skip-gram 两个模型的损失函数,差异是非常明显的。因为 skip-gram 模型的预测次数和上下文单词数量一样多,所以它的损失函数需要求各个上下文单词对应的损失的总和,而CBOW模型只需要求目标词的损失。
两种模型的选择:
从单词的分布式表示的准确度来看, 在大多数情况下,skip-grm 模型的结果更好。特别是随着语料库规模的增大,在低频词和类推问题的性能方面,skip-gram 模型往往会有更好的表现。
从学习速度来看, CBOW 模型比 skip-gram 模型要快。这是因为 skip-gram 模型需要根据上下文数量计算相应个数的损失,计算成本变大。
skip-gram 模型根据一个单词预测其周围的单词,这是一个非常难的问题。经过这种更难的问题的锻炼,skip-gram 模型能提供更好的 单词的分布式表示。
因此还是会选择 skip-gram 模型。
3.5.3 基于计数与基于推理
两种方法在学习机制上存在显著差异:基于计数的方法通过对整个语料库的统计数据进行一次学习来获得单词的分布式表示,而基于推 理的方法则反复观察语料库的一部分数据进行学习(mini-batch 学习)。
- 考虑需要向词汇表添加新词并更新单词的分布式表示的场景。基于计数的方法需要从头开始计算。即便是想稍微修改一下单词的分布式表示,也需要重新完成生成共现矩阵、进行 SVD 等一系列操作。 相反,基于推理的方法(word2vec)允许参数的增量学习。具体来说,可以将之前学习到的权重作为下一次学习的初始值,在不损失之前学习到的经验的情况下,高效地更新单词的分布式表示。在这方面,基于推理的方法 (word2vec)具有优势。
- 两种方法得到的单词的分布式表示的性质和准确度的差异。就分布式表示的性质而言,基于计数的方法主要是编码单词的相似性,而 word2vec(特别是 skip-gram 模型)除了单词的相似性以外,还能理解更复杂的单词之间的模式。
- 基于推理的方法和基于计数的方法存在关联性。具体地说,使用了 skip-gram 和下一章介绍的 Negative Sampling 的模型被证明与对整个语料库的共现矩阵(实际上会对矩阵进行一定的修改)进行特殊矩阵分解的方法具有相同的作用。换句话说,这两个方法论(在 某些条件下)是“相通”的。
有一个常见的误解,那就是基于推理的方法在准确度方面优于基于计数的方法。实际上,有研究表明,就单词相似性的定量评价而言,基于推理的方法和基于计数的方法难分上下(具体参考附录论文[25])。
在 word2vec 之后,有研究人员提出了 GloVe 方法。GloVe 方法融合了基于推理的方法和基于计数的方法。该方法的思想是,将整个语 料库的统计数据的信息纳入损失函数,进行 mini-batch 学习(具体请参考附录论文 [27])。据此,这两个方法论成功地被融合在了一起。