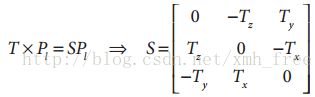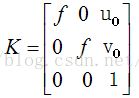计算机视觉中的对极几何及相机自检校

一 空间坐标关系

         计算机视觉领域的三维重建坐标系一般包括四个：像素坐标系、图像坐标系、相机坐标系以及世界坐标系。其对应关系如图-1所示：

 

                            

                                                                                   图-1

 

         其中，O0-UV为像素坐标系；O1-XY为图像坐标系；O-XcYcZc为相机坐标系；O-XwYwZw为世界坐标系。

         如图所示，相机的成像过程可通过四个坐标系(世界坐标系、相机坐标系、图像坐标系、像素坐标系)之间的三次转换来表达。

        三个转换过程如下所述：

        (1) 首先将世界坐标系中的信息转换到相机坐标系中；

        (2) 然后将相机坐标系中的信息转换到图像坐标系中；

        (3) 最后则是由图像坐标系中的信息转换到像素坐标系中。

        如下式所示：

                                                     (1)    

 

                                  (2)

 

       矩阵K包含相机的内参数，矩阵H包含相机的外参数（即旋转矩阵R和平移向量T）。内参K矩阵的含义是建立起“相机坐标系”与“像素坐标系”之间的转换关系，外参H矩阵的含义是建立起“世界坐标系”与“相机坐标”之间的转换关系。

 

二 对极几何

1 基本矩阵的推导

         对极几何关系的含义是：在一个物体的两幅图像中，匹配点(不同图像中来自同一个空间点的投影称为匹配点)的相对位置受到两个图像平面空间几何关系的约束，这种约束关系在计算机视觉中就称为对极几何关系，它可以用基础矩阵来准确地表达。

        本质上，两幅图像之间的对极几何是图像平面与以基线(连接两摄像机中心的直线)为轴的平面束的交的几何。如图-2所示：

                        

                                                                                图-2

 

        在推导基本矩阵之前，需要先了解另一个重要的矩阵“本质矩阵”，常用E表示。它包含了物理空间中两个摄像机相关的旋转(R)和平移信息(T)。T和R描述了一台摄像机相对于另外一台摄像机在全局坐标系中的相对位置。本征矩阵E是单几何意义上的，与成像仪无关，它将左摄像机观测到的点P的相机坐标和右摄像机观测到的相同的点的位置关联起来，如图-3所示：

                             

                                                                                 图-3

 

        对于左相机系我们选用Ol-XYZ为左摄像机坐标系（其中投影中心Ol为原点，Z轴为光轴的方向），同样的对于右相机，我们采用同样的方法建立右摄像机坐标系。那么图-3中点pl和pr分别相对于各自的摄像机有各自的坐标，我们不妨设为pl(x1,y1,z1)和pr(x2,y2,z2)。

        注意，这里要说一下Pl、Pr和pl、pr的区别，前者表示物方点P在两个成像仪上所成的像在左右两个摄像机坐标系下的坐标，后者表示点P在左右两个摄像机坐标系下的坐标。给定点P，我们将要推导点P在两个成像仪的观测位置pl和pr之间的关系，pl和pr是在两个摄像机坐标系中观察到的点的物理坐标，利用对极几何可以将它们联系起来。

        我们知道点Pl是点P在左摄像机Ol为中心的坐标系下的坐标。Pr是P点在右摄像机Or为中心的坐标系下的坐标。我们令左摄像机Ol为坐标系的中心，Or相对于Ol的坐标为T，R表示旋转矩阵，那么Pr=R(Pl-T)。Pr为3×1的列向量(相对于中心点),R为3×3的旋转矩阵，P1为3×1的列向量，T也是3×1的列向量（因为Pr,Pl,T都是三维点）。

 

                       

                                                                                  图-4

 

 

        公式Pr=R(Pl-T),Pl表示在以Ol为原点的坐标，Pr表示以Or为原点的坐标。T=目标原点—摄像机原点。那么如果右摄像机的原点为T,那么就相当于右摄像机为“目标原点”，左摄像机为“摄像机原点”，这就和旋转矩阵和平移向量部分相吻合。

       我们选取左摄像机的投影中心Ol为坐标系的中心，即Ol为原点(0,0,0)，那么点Pl和点T，就可以表示为相对于Ol的向量。那么极面上就有向量Pl和T,我们知道右手准则，与P1和T相垂直的向量和法向量同相，并且为P1和T的叉乘。那么通过点T的所有可能点Pl,以及包含这两个向量的方程表示如下：

                                                                                                                   (3)

        将公式Pr=R(Pl-T)， 即Pl-T=R-1Pr，并且R-1=Rt（R是正交阵）得：

                                                                                                                         (4)

        总是可以将叉积写成矩阵相乘的形式，故定义矩阵S为:

                                                                  (5)

 

        这样就推导出了第一个结果，将上式带入到叉积公式中，得到：

                                                                                                                                         (6)

 

        乘积RS就是我们的定义的本征矩阵，我们可以写成下面的简洁形式：

                                                                                                                                         (7)

        上述公式给出了点P在两个坐标系下的坐标之间的关系，但是我们要求解的是点P 在两个成像仪上的投影点在两个坐标系下的关系。那么，我们利用投影方程（几何关系）即：

 

                                                                                                    (8)

 

         将上述两个投影方程带入到上面的公式，并且除以ZlZr/flfr，得到最终的公式：

                                                                                                                                                 (9)

 

        在实际应用中，我们通常只对像素坐标感兴趣。为了将像素坐标和极线联系起来，即必须将两台摄像机的内参入信息引入进来，这就是基本矩阵F。

我们用q（像素坐标）代替本征矩阵公式(6)中的P,已知q=K*P，将本质矩阵表达示为

                                                                                               (10)

       即 ：

                                                                                             (11)

      从而，得到：

                                                                                                                (12)

       故：

                             且                                                                (13)

 

       观察摄像机内参数矩阵K，如果图像没有畸变，即cx,cy为0，并且焦距进行了归一化处理，那么K就成了单位阵，此时本征矩阵F就等于基础矩阵E，即F=E。

 

2 基本矩阵的意义

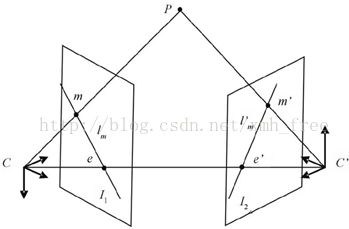
       基本矩阵F描述的是图像平面上的像素坐标系之间的同名像点的几何关系，已知基础矩阵F和图像对中任意一幅图像上的一个点x，可以确定另一图像上的x的对应点x’所在的直线，这条直线称作“对极线”。图像对之间的所有同名点x和x’都各自对应着一条极线，同幅图像内的所有极线交于一点e，成为“对极点”，极点本质上是相邻相机的投影中心S在图像上的像点。

       因此，图像点x反向投影成三维空间的一条射线，它由第一个摄像机中心C和x确定，这条射线在第二个视图中被映射成一条直线lx′，即是对应于x的对极线，点x在I2上的对应点x′必然落在其对极线lx′上。同理，在第一个视图中也存在着一条对应于x′的对极线lx，它们都分别通过其对应的对极点，这样就把对应点在相应二维平面上的搜索范围降到一维，同样也可据此对初始匹配点进行优化。

    

三 相机自检校

       相机标定主要确定相机的内参数，一般分为两种方式：基于标定物的检校方法和自检校方法。基于物方标定物的检校方法通过物方控制点和图像点之间的对应关系估计相机矩阵M，从而得到相机的内外参数，标定精度一般较高，但是使用范围受限。相机自检校的方法不需要已知的物方控制点，只需要根据图像信息即可解算得到相机内参数，精度一般不如基于控制场的标定精度，但使用方便，适用范围广。

       基于标定物的标定方法是一种传统的标定方法，这里不作介绍。下面详细介绍一种自标定算法，其主要思想是利用基本矩阵的信息获取相机内参矩阵。

这里，我们采用的相机内参矩阵模型为：

                     

 

          即默认相机像元长宽比为1，相机水平竖直轴间严格垂直S=1。

          我们假设左右相机的投影矩阵分别为：

                           和    

          则投影方程可以表示为(14)和(15)：

                                                                                                   (14)       

                                                                                               (15)

          其中Xp是齐次坐标Xp = (X  1) = (x  y  z  1)，于是有： 

                                                                                                                          (16)  

                                                                                                                       (17)

         将式(16)和(17)消去X得：

                                                                    (18)

         将式(18)右边向量记作m，即：

                                                                                                                      (19)

 

         将式(19)定义的m左叉乘式(18)得：

   

                                                                                                    (20)

          由式(20)可知，该式与向量正交，将左乘式(20)可得一下重要关系：

                                                                                                                        (21)

          其中，是基本矩阵F的又一表达式。

         将左右相机矩阵P1和P2的特殊形式代入由式(21)中隐含的基本矩阵F表达形式，可以得到式(22)：

                                                                                                                          (22)

         然后，由（其中e’为极点），可以得到，相机自检校的基本方程式(23)：

 

                                                                                                              (23)

        此时，默认三张连续图像的内参数只有焦距f的变化，共5个参数，而每对图像估计的基本矩阵可以提供两个约束方程，因此，三张图像可以得到6个等式，即可解除三张图像的内参矩阵K1、K2和K3，具体解法不再作详细阐述，重在介绍算法的思想。详细信息可阅读Zetao Jiang, Shutao Guo和 Lianggang Ji的论文“Sequences Images Based Camera Self-calibration Method ”。

 

 

 

参考资料：

1 http://blog.csdn.net/raby_gyl/article/details/17174751.

2 Sequences Images Based Camera Self-calibration Method ,Zetao Jiang, Shutao Guo, Lianggang Ji.