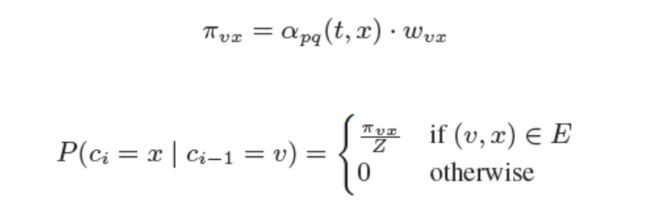从零开始一文理解Graph Embedding

先说下不同embedding的区别是什么：

1. DeepWalk：采用随机游走，形成序列，采用skip-gram方式生成节点embedding。
2. node2vec：不同的随机游走策略，形成序列，类似skip-gram方式生成节点embedding。
3. LINE：捕获节点的一阶和二阶相似度，分别求解，再将一阶二阶拼接在一起，作为节点的embedding
4. struc2vec：对图的结构信息进行捕获，在其结构重要性大于邻居重要性时，有较好的效果。
5. SDNE：采用了多个非线性层的方式捕获一阶二阶的相似性。

基本知识

为了更好的理解不同图编码机制，首先要了解一些基础知识。

图的基础知识/什么是Graph Embedding

图：Graph=（V，E）
v：顶点（数据元素）的有穷非空集合；
E：边的有穷集合。

在上图中v1-v5都可以编码成一个d维的embedding向量。只要给定d维度，而由神经网络自动图中节点的embedding这一过程，就叫做Graph Embedding

随机游走

基本思想
从一个或一系列顶点开始遍历一张图。在任意一个顶点，遍历者将以概率1-a游走到这个顶点的邻居顶点，以概率a随机跳跃到图中的任何一个顶点，称a为跳转发生概率，每次游走后得出一个概率分布，该概率分布刻画了图中每一个顶点被访问到的概率。用这个概率分布作为下一次游走的输入并反复迭代这一过程。当满足一定前提条件时，这个概率分布会趋于收敛。收敛后，即可以得到一个平稳的概率分布。

最经典的一维随机游走问题有赌徒输光问题和酒鬼失足问题。

（1）赌徒在赌场赌博，赢的概率是p，输的概率1-p，每次的赌注为1元，假设赌徒最开始时有赌金1元，赢了赌金加1元，输了赌金减1元。问赌徒输光的概率是多少？
（2）一个醉鬼行走在一头是悬崖的道路上，酒鬼从距离悬崖仅一步之遥的位置出发，向前一步或向后退一步的概率皆为1/2，问酒鬼失足掉入悬崖的概率是多少？

图的随机游走

上图中的random walk 就是形成了一条随机游走链（N1,N2,N3,N4)，其中N1的又有本身的编码，N1=(a1, a2, a3)，即一个3维的embedding.

在上图中发Φ表示embedding， |V|xd即v个节点乘以d维编码，例如，上文提到的N1节点 N1=(a1, a2, a3)就是3维编码。

SkipGram
SkipGram就是给定一个中心词，去预测它的上下文
假设在我们的文本序列中有5个词，[“the”，“man”，“loves”，“his”，“son”]。

假设我们的窗口大小skip-window=2，中心词为“loves”，那么上下文的词即为：“the”、“man”、“his”、“son”。这里的上下文词又被称作“背景词”，对应的窗口称作“背景窗口”。

跳字模型能帮我们做的就是，通过中心词（target word）“loves”，生成与它距离不超过2的背景词（context）“the”、“man”、“his”、“son”的条件概率，用公式表示即：

进一步，假设给定中心词的情况下，背景词之间是相互独立的，公式可以进一步得到

用概率图表示为：

可以看得出来，这里是一个一对多的情景，根据一个词来推测2m个词，（m表示背景窗口的大小），上图窗口大小为2.

DeepWalk

DeepWalk 是network embedding的开山之作，它将NLP中词向量的思想借鉴过来做网络的节点表示，提供了一种新的思路.了解了随机游走后DeepWalk算法就变得简单了，DeepWalk最主要的贡献就是他将Network Embedding与自然语言处理中重要的Word Embedding方法Word2Vec联系了起来，使得Network Embedding问题转化为了一个Word Embedding问题。

转化方法其实很简单，就是随机游走。如下图所示，DeepWalk通过从每个结点出发n_walks次，每一步都采取均匀采样的方式选择当前结点的邻接结点作为下一步的结点随机游走。当游走的路径长度达到walk_length后，停止一次游走。这样就生成了一个个游走的序列，每个序列都称为一个walk。每个walk都被当成Word2Vec中的一个句子，而每个结点都是Word2Vec中的一个词。 下图中每一个圆都代表一个d维向量。

LINE

LINE不再采用随机游走的方法。相反，他在图上定义了两种相似度——一阶相似度与二阶相似度。
一阶相似度：一阶相似度就是要保证低维的嵌入中要保留两个结点之间的直接联系的紧密程度，换句话说就是保留结点之间的边权，若两个结点之间不存在边，那么他们之间的一阶相似度为0。例如下图中的6、7两个结点就拥有很高的一阶相似度。
二阶相似度：二阶相似度用一句俗话来概括就是“我朋友的朋友也可能是我的朋友”。他所比较的是两个结点邻居的相似程度。若两个结点拥有相同的邻居，他们也更加的相似。如果将邻居看作context，那么两个二阶相似度高的结点之间拥有相似的context。这一点与DeepWalk的目标一致。例如下图中的5、6两点拥有很高的二阶相似度。

总而言之，一阶：局部的结构信息；二阶：节点的邻居。共享邻居的节点可能是相似的。

下面给出求一阶相似性的方法：

下面是求二阶相似性的方法：

一阶二阶embedding训练完成之后，如果将first-order和second-order组合成一个embedding，即直接拼接的方法。

Node2vec

Node2Vec是一份基于DeepWalk的延伸工作，它改进了DeepWalk随机游走的策略。
Node2Vec认为，现有的方法无法很好的保留网络的结构信息，例如下图所示，有一些点之间的连接非常紧密(比如u, s1, s2, s3, s4)，他们之间就组成了一个社区(community)。网络中可能存在着各种各样的社区，而有的结点在社区中可能又扮演着相似的角色(比如u与s6)。

那么如何达到这样的两种随机游走策略呢，这里需要用到两个超参数p和q用来控制深度优先策略和广度优先策略的比重，如下图所示：

其中d(t, x)代表t结点到下一步结点x的最短路，最多为2。

当d(t, x)=0时，表示下一步游走是回到上一步的结点；
当d(t, x)=1时，表示下一步游走跳向t的另外一个邻居结点；
当d(t, x)=2时，表示下一步游走向更远的结点移动。

而Node2Vec同时还考虑了边权w的影响，所以最终的偏置系数以及游走策略为:

其具体算法如下所示：

DFS，即q值⼩，探索强。会捕获homophily同质性节点，即相邻节点表示类似
BFS，即p值⼩，保守周围。会捕获结构性，即某些节点的图上结构类类似

Struc2vec

之前的node embedding的方式，都是基于近邻关系，但是有些节点没有近邻，但也有相似的结构性。deepwalk和node2vec 可以成功应用于分类任务，但在结构相关任务中往往失败， 主要原因在于：大多数真实网络中的许多节点特征表现出很强的同质性， 具有给定特征的节点的邻域更有可能具有相同的特征，而我们提出的struc2vec的关键思想是：

1、 评估独立于节点和edge的节点之间的结构相似性，以及它们在网络中的位置。（即struc2vec不依赖于节点互相接近）；

2、 建立一个层次结构来衡量结构相似性，允许对结构相似性的含义有越来越严格的定义， 特别是在这个层次结构的底部，节点之间的结构相似性仅取决于它们的度， 而在层次结构的顶部，相似性取决于整个网络，

3、 为节点生成随机上下文，这些节点是通过遍历多层图（而不是原始网络)的加权随机游走得到，因此，经常出现在相似上下文中的两个节点可能具有相似的结构。 这种上下文可以通过语言模型来学习节点的潜在表示；（这里的意思应该对原图做了另一种层次的表示，然后在新的层次图结构上做加权随机游走）

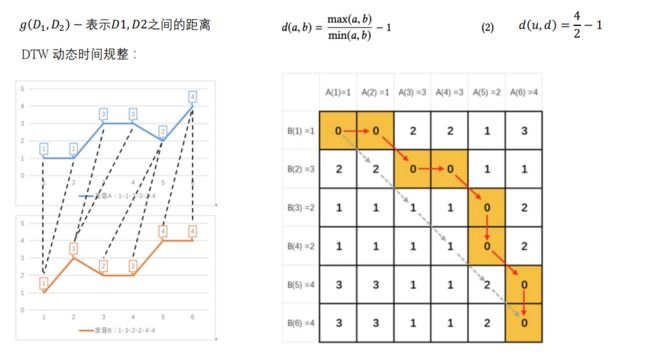
DTW动态时间规划

具体而言是一种计算距离的公式：

举个例子：
a=(1,2,3), b=(2,1,2)
那么：
d(a,b) = max((1,2,3), (2,1,2)) / min((1,2,3), (2,1,2)) = 3 / 1 = 3

1、根据不同距离的邻居信息分别算出每个节点对的结构相似度，这涉及到了不同层次的结构相似度的计算，到这里就可以较好的理解层次化结构具体是什么意思了；

2、构造一个加权多层图，其中网络中的所有节点都存在于每一层中（完全同一张图），并且每一层都对应于测量结构相似性时的层次结构存在级别上的差异。 此外，每一层中每个节点对之间的edge权重与其结构相似度成反比；

3、 使用多层图为每个节点生成上下文。 特别是，多层图上的有偏随机游走（edge带权，不是完全随机游走的）用于生成节点序列，这个 序列中很可能包括在结构上更相似的节点。

4、使用word2vec的方法对采样出的随机游走序列学习出每个节点的节点表示。

SDNE (Structural Deep Network Embedding）

SDNE中的相似度定义和LINE是一样的。简单来说，1阶相似度衡量的是相邻的两个顶点对之间相似性。2阶相似度衡量的是，两个顶点他们的邻居集合的相似程度。
之前的Deepwalk，LINE，node2vec，struc2vec都使用了浅层的结构，浅层模型往往不能捕获高度非线性的网络结构。即产生了SDNE方法，使用多个非线性层来捕获node的embedding

一阶公式：

二阶公式：

将一阶相似性与二阶相似性合并：

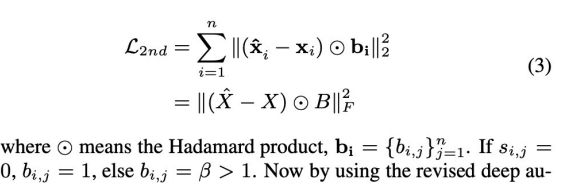
示例代码

下面给出的是deepwalk的实现代码：

import numpy as np

from ge.classify import read_node_label, Classifier
from ge import DeepWalk
from sklearn.linear_model import LogisticRegression

import matplotlib.pyplot as plt
import networkx as nx
from sklearn.manifold import TSNE


def evaluate_embeddings(embeddings):
    X, Y = read_node_label('../data/wiki/wiki_labels.txt')
    tr_frac = 0.8
    print("Training classifier using {:.2f}% nodes...".format(
        tr_frac * 100))
    clf = Classifier(embeddings=embeddings, clf=LogisticRegression())
    clf.split_train_evaluate(X, Y, tr_frac)


def plot_embeddings(embeddings,):
    X, Y = read_node_label('../data/wiki/wiki_labels.txt')

    emb_list = []
    for k in X:
        emb_list.append(embeddings[k])
    emb_list = np.array(emb_list)

    model = TSNE(n_components=2)
    node_pos = model.fit_transform(emb_list)

    color_idx = {}
    for i in range(len(X)):
        color_idx.setdefault(Y[i][0], [])
        color_idx[Y[i][0]].append(i)

    for c, idx in color_idx.items():
        plt.scatter(node_pos[idx, 0], node_pos[idx, 1], label=c)
    plt.legend()
    plt.show()


if __name__ == "__main__":
    # G = nx.read_edgelist('../data/wiki/Wiki_edgelist.txt',
    #                      create_using=nx.DiGraph(), nodetype=None, data=[('weight', int)])
    # nx.draw(G, node_size=10, font_size=10, font_color="blue", font_weight="bold")
    # plt.show()
    import pandas as pd
    df = pd.DataFrame()
    df['source'] = [str(i) for i in [0,1,2,3,4,4,6,7,7,9]]
    df['target'] = [str(i) for i in [1,4,4,4,6,7,5,8,9,8]]

    G = nx.from_pandas_edgelist(df,create_using=nx.Graph())

    model = DeepWalk(G, walk_length=50, num_walks=180, workers=1)
    model.train(window_size=10, iter=3,embed_size=2)
    # model = DeepWalk(G, walk_length=10, num_walks=80, workers=1)
    # model.train(window_size=5, iter=3,embed_size=128)
    embeddings = model.get_embeddings()
    #print(embeddings)
    x,y = [],[]
    print(sorted(embeddings.items(), key=lambda x: x[0]))
    for k,i in embeddings.items():
        x.append(i[0])
        y.append(i[1])
    plt.scatter(x,y)
    plt.show()

    # evaluate_embeddings(embeddings)
    # plot_embeddings(embeddings)

参考文献

【1】 https://zhuanlan.zhihu.com/p/64991884
【2】https://blog.csdn.net/qq_43186282/article/details/114585885
【3】https://zhuanlan.zhihu.com/p/162177874