Python数据结构与算法-树
一、树的概念
详情见 https://blog.csdn.net/little_limin/article/details/129845592
Python数据结构与算法-堆排序(NB组)—— 一、树的基础知识
二、树的实例:模拟文件系统
1、树的存储
树结构也是链式存储的,与链表的结构相似,只是树存在多个子节点,不是线性的,存在一堆多的情况。与双链表相似,只不过链表节点对应的下一个节点只有一个,树节点对应的孩子节点很多,需要用列表[]存储。
(1)树节点代码实现
# 树节点的类
class Node(): # 创建文件节点的类,及其属性(父节点,孩子节点)
def __init__(self, name, type = "dir"): # 节点初始属性,文件名,文件类型
self.name = name # 文件名
self.type = type # 文件类型
# 文件相互间关系
self.children = [] # 孩子节点,孩子节点可以有很多,所以是列表
self.parent = None # 父节点,父节点只有一个的,不一定需要有这个指向
# print测试
n = Node("hello") #父节点
n2 = Node("world") #孩子节点1
n3 = Node("yoyo") # 孩子节点2
# 孩子节点与父节点关联
n.children.append(n2)
n.children.append(n3)
n2.parent = n
n3.parent = n
# 打印孩子节点的属性
for nm in n.children:
print(nm.name)(2)输出结果
world
yoyo2、模拟文件系统
(1)代码实现
# 树的实例:模拟文件系统
# 树是链式存储
class Node(): # 创建文件节点的类,及其属性(父节点,孩子节点)
def __init__(self, name, type = "dir"): # 节点初始属性,文件名,文件类型
self.name = name # 文件名
self.type = type # 文件类型
# 文件相互间关系
self.children = [] # 孩子节点,孩子节点可以有很多,所以是列表
self.parent = None # 父节点,父节点只有一个的,不一定需要有这个指向
def __repr__(self): # 内置函数,返回值
return self.name # 返回名字
class FileSystemTree(): # 创建文件根目录——数据结构(树)
def __init__(self) -> None: # 树的属性
self.root = Node("/") # 树的根节点,类似于链表的head结点
self.now = self.root # now指针,当前目录
def mkdir(self,name): # 当前目录创建文件
# 保证name以/结尾
if name[-1] != "/": # name这个字符串的最后一位不是斜杠
name += "/" # 在name的最后加上斜杠
new_dir = Node(name) # 创建文件节点
# 创建与当前文件夹的连接
self.now.children.append(new_dir)
new_dir.parent = self.now
def ls(self): # 展现当前目录下的所有子目录
return self.now.children # 返回子目录列表
def cd(self,name): # 切换目录(到子目录),支持向上返回
# 判断是否为文件夹
if name[-1] != "/":
name += "/"
if name == "../": #当前目录
self.now = self.now.parent # 返回目录到上级
return
# 找到和name相同的文件
for child in self.now.children:
if child.name == name:
self.now = child # 切换目录到child
return # 输出
# 子目录中无该文件夹,报错
raise ValueError("invaild dir")
tree = FileSystemTree() # 创建树
# 新建文件夹
tree.mkdir("Var/")
tree.mkdir("bin/")
tree.mkdir("usr/")
print(tree.ls()) # 展示当前子目录
# 切换到子目录
tree.cd("bin/")
tree.mkdir("python/") # 子目录中创建文件夹
print(tree.ls()) # 展示当前子目录
# 切换回上级目录
tree.cd("../")
print(tree.ls()) # 展示当前子目录(2)代码结果
[Var/, bin/, usr/]
[python/]
[Var/, bin/, usr/]3、模拟文件代码相关知识点
(1)__repr__ 和__str__ 内置函数的用法和示例
1)__repr__的作用
输出实例对象时,其内容由__repr__的返回值决定。
class Test:
def __repr__(self) -> str:
return "hello"
t = Test()
print(t)输出结果
hello可以看到,当打印实例对象的时候,打印的结果就是__repr__的返回值。如果不加定义__repr__则会默认使用object的__repr__函数,返回如下:
<__main__.Test object at 0x0000023573CF0700>2)__str__作用
与__repe__作用相同,只不过__str__要更猛一点,当你的类中同时重写了__str__和__repr__后,那么当你打印实例对象的时候,python底层会优先执行实例对象.__str__()。
class Test:
def __repr__(self) -> str:
return "repr"
def __str__(self) -> str:
return "str"
t = Test()
print(t)输出结果
str通过上面这个例子可以看到,输出的是__str__的返回值(__repr__没抢过__str__)。
(2)__str__和__repr__区别
在代码编辑器中执行print()函数,python优先调用print(实例对象.__str__());而当在运行终端直接敲实例对象的时候,python底层执行的其实是实例对象.__repr__()。
示例1:在终端直接打印
>>> from text import Test
>>> t = Test()
>>> t
repr
>>> print(t)
str示例2:在编辑器print()
class Test:
def __repr__(self) -> str:
return "repr"
def __str__(self) -> str:
return "str"
t = Test()
print(t)输出结果:
str(3)文件的相对路径和绝对路径
相对路径从当前目录到文件所在位置;
绝对路径从根目录开始到文件所在地。
(4)python的"./"、"../"和"/"路径
./代表目前文件所在的目录。
. ./代表目前文件的上一层目录。
/代表根目录。
三、二叉树
1、概念
详情见 https://blog.csdn.net/little_limin/article/details/129845592
Python数据结构与算法-堆排序(NB组)—— 二、二叉树的基础知识
2、二叉树的存储
(1)二叉树的链式存储
将二叉树的节点定义为一个对象,节点之间通过类似链表的链接方式来连接。
(2)节点存储代码
class BiTreeNode: # 二叉树
def __init__(self,data): # data:节点数据
self.data = data
self.lchild = None # 左孩子
self.rchild = None # 右孩子3、二叉树代码实现
# 二叉树的简单实现
class BiTreeNode(): # 二叉树节点
def __init__(self,data) -> None:
self.data = data
self.lchild = None
self.rchild = None
# 定位节点
a = BiTreeNode("A")
b = BiTreeNode("B")
c = BiTreeNode("C")
d = BiTreeNode("D")
e = BiTreeNode("E")
f = BiTreeNode("F")
g = BiTreeNode("G")
# 节点关系链接
e.lchild = a
e.rchild = g
a.rchild = c
c.lchild = b
c.rchild = d
g.rchild = f
# 根节点
root = e
print(root.lchild.rchild.data)结果输出
C4、二叉树的遍历
以上图举例,树的遍历如何实现。
(1)二叉树遍历方式
前序遍历:EACBDGF 从根节点开始,先左孩子再右孩子。
中序遍历:ABCDEFG
后序遍历:BDCAFGE
层次遍历:EAGCFBD
(2)前序遍历代码实现
在二叉树代码实现的基础代码上,增加以下代码,以下代码为前序遍历主代码。
# 根节点
root = e
# 前序遍历
def pre_order(root):
if root: # root不为空
print(root.data, end = ',')
pre_order(root.lchild) # 访问左孩子
pre_order(root.rchild) # 访问右孩子
pre_order(e) # 从e开始前序遍历输出结果
E,A,C,B,D,G,F,(3)中序遍历代码实现
中序遍历可以理解为将树结构“拍扁”,与前序遍历的区别仅在print打印的位置不同。
# 中序遍历
def in_order(root):
if root: # root不为空,递归结束条件
in_order(root.lchild) # 访问左孩子
print(root.data, end = ',') # 打印本身
in_order(root.rchild) # 访问右孩子
in_order(root) # 从e开始前序遍历输出结果
A,B,C,D,E,G,F,递归原理
s1.首先,运行E的左孩子所在的子树,打印E,再运行E的右孩子所在的子树。
s2.进入E的左孩子的子树,A没有左孩子,打印A,运行A的右孩子。
s3.进入A的右孩子的子树,先运行C的左孩子,打印C,运行C的右孩子。
s4.进入C的左孩子的子树,打印了B;进入C的右孩子的子树,打印了D。
s5,进入E的右孩子的子树,依旧同以上步骤,得到G和F。
(4)后序遍历
# 后序遍历
def post_order(root):
if root: # root不为空,递归结束条件
post_order(root.lchild) # 访问左孩子
post_order(root.rchild) # 访问右孩子
print(root.data, end = ',') # 打印本身
post_order(root) # 从e开始前序遍历输出结果
B,D,C,A,F,G,E,递归原理
运行的顺序从左往右,与中序遍历的原理类似。先运行左孩子所在子树,再运行右孩子所在子树,最后才打印本身。
(5)层次遍历
# 层次遍历——广度优先搜索
from collections import deque # 队列模块
def level_order(root):
queue = deque() # 新建队列
queue.append(root) # 根节点入队
while len(queue) > 0: # 队列不空
node = queue.popleft() # 节点出队
print(node.data, end = ',') # 得到节点的值
if node.lchild: # 节点的左孩子存在
queue.append(node.lchild) # 左孩子进入队列
if node.rchild: # 节点的右孩子存在
queue.append(node.rchild) # 右孩子入队
level_order(root)输出结果
E,A,G,C,F,B,D,代码实现原理
使用单向队列的性质,节点出队时,其对应的孩子节点入队。例如(以本节遍历二叉树为例):
[E]:根节点入队
E,[A,G]:E出队,对应的左孩子A和右孩子入队
E,A,[G,C]:A出队,A的右孩子C入队
E,A,G,[C,F]:G出队,G的右孩子F入队
E,A,G,C,[F,B,D]:C出队,C的左孩子B,右孩子D出队
E,A,G,C,F,[B,D]:F出队,F没有孩子节点
E,A,G,C,F,B,[D]:B出队,B没有孩子节点
E,A,G,C,F,B,D,[]:D出队,D没有孩子节点,队列为空,结束循环。
三、二叉搜索树
1、概念
二叉搜索树是一棵二叉树且满足性质:设x是二叉树的一个节点。如果y是x左子树的一个节点,那么y.key ![]() x.key;如果y是x右子树的一个节点,那么y.key
x.key;如果y是x右子树的一个节点,那么y.key ![]() x.key。
x.key。
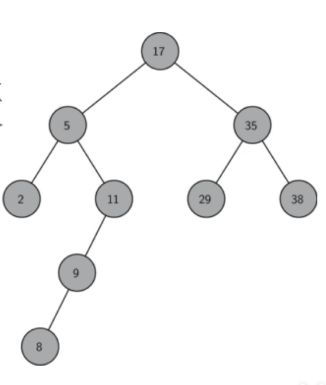
如下图为一棵二叉搜索树:
二叉搜索树的操作:查询、插入、删除
查询和插入的时间复杂度都为O(logn),删除操作较为复杂后面会具体分析。
2、二叉搜索树:插入
(1)递归实现插入
当插入值小于当前节点的值,当前节点的左孩子(左孩子子树)是插入值的节点;当插入值大于当前节点的值,当前节点的右孩子(右孩子子树)是插入值的节点;若该值插入的位置不存在节点或该值与当前节点值相同,则创建新的节点或覆盖该节点。
# 二叉搜索树的用递归写插入函数
class BiTreeNode(): # 二叉树节点
def __init__(self, data) -> None: # 属性
self.data = data # 树的值
self.lchild = None # 左孩子
self.rchild = None # 右孩子
self.parent = None # 父节点
# 二叉搜索树 binary search tree
class BST():
def __init__(self): # 创建空树
self.root = None # 根节点为空
# 递归插入
def insert(self, node, val): # node是指二叉树中当前指向的节点,初始一般为根节点,val是指插入的值
if not node or node.data == val: # 空树或节点的值与插入的值相同
node = BiTreeNode(val) # 创建一个节点插入到树中(最后一步)或者是插入的值的节点直接与原节点相重合
elif val < node.data: # 插入的值小于当前节点的值
# 往当前节点的左边插,当前节点的也就往左孩子找
node.lchild = self.insert(node.lchild,val) # 左孩子为根节点的子树上,node.lchild(当前点的左孩子) = node(插入的节点)
node.lchild.parent = node # 与父节点的连接
else: # val > node.data
node.rchild = self.insert(node.rchild,val) # 当前节点的右孩子是插入的节点
node.rchild.parent = node
return node # 返回
# 前序遍历
def pre_order(self, root):
if root: # root不为空
print(root.data, end = ',')
self.pre_order(root.lchild) # 访问左孩子
self.pre_order(root.rchild) # 访问右孩子
tree = BST()
node = BiTreeNode(10) # 树的根节点
# 插入数值
tree.insert(node,5)
tree.insert(node,19)
tree.insert(node,8)
tree.insert(node,3)
tree.pre_order(node)输出结果
10,5,3,8,19,(2)普通方式实现插入
# 二叉搜索树普通办法写插入函数
class BiTreeNode(): # 二叉树节点
def __init__(self, data) -> None: # 属性
self.data = data # 树的值
self.lchild = None # 左孩子
self.rchild = None # 右孩子
self.parent = None # 父节点
# 二叉搜索树 binary search tree
class BST():
def __init__(self, li=None): # 创建树
self.root = None # 根节点为空
# 创建二叉搜索树
if li:
for val in li:
self.insert_no_dec(val) # 循环插入值
def insert_no_dec(self,val): # 非递归
p = self.root # 创建指针p,p起始指向根节点
if not p: # p指向节点为空,空树,
self.root = BiTreeNode(val) # 创建根节点
return
while True: # 循环
if val < p.data: # 插入值小于p指向节点的值
if p.lchild: # 左孩子节点存在
p = p.lchild # 指针移动至新的节点
else: # 左孩子不存在
p.lchild = BiTreeNode(val) # 插入值
p.lchild.parent = p # 连接父节点
return # 结束循环,返回
elif val > p.data: # 插入值大于p指向节点的值
if p.rchild: # 右孩子存在
p = p.rchild # 指针移动至新节点
else: # 右孩子不存在
p.rchild = BiTreeNode(val) # 插入值
p.rchild.parent = p # 连接父节点
return # 结束循环,返回
else: # val == p.data
return # 不用插入
# 前序遍历
def pre_order(self,root):
if root: # root不为空
print(root.data, end = ',')
self.pre_order(root.lchild) # 访问左孩子
self.pre_order(root.rchild) # 访问右孩子
# 中序遍历
def in_order(self, root):
if root: # root不为空,递归结束条件
self.in_order(root.lchild) # 访问左孩子
print(root.data, end = ',') # 打印本身
self.in_order(root.rchild) # 访问右孩子
# 后序遍历
def post_order(self, root):
if root: # root不为空,递归结束条件
self.post_order(root.lchild) # 访问左孩子
self.post_order(root.rchild) # 访问右孩子
print(root.data, end = ',') # 打印本身
tree = BST([4,6,7,9,2,1,3,5,8]) # 对象实例化
# 遍历二叉树
tree.pre_order(tree.root)
print("")
tree.in_order(tree.root)
print("")
tree.post_order(tree.root)输出结果:
4,2,1,3,6,5,7,9,8,
1,2,3,4,5,6,7,8,9,
1,3,2,5,8,9,7,6,4,说明:中序遍历的二叉搜索树一定是升序输出的
3、二叉搜索树:查询
查询函数的原理与插入函数的原理基本一致。
import random
class BiTreeNode(): # 二叉树节点
def __init__(self, data) -> None: # 属性
self.data = data # 树的值
self.lchild = None # 左孩子
self.rchild = None # 右孩子
self.parent = None # 父节点
# 二叉搜索树 binary search tree
class BST():
def __init__(self, li=None): # 创建树
self.root = None # 根节点为空
# 创建二叉搜索树
if li:
for val in li:
self.insert_no_dec(val) # 循环插入值
def insert_no_dec(self,val): # 非递归插入
p = self.root # 创建指针p,p起始指向根节点
if not p: # p指向节点为空,空树,
self.root = BiTreeNode(val) # 创建根节点
return
while True: # 循环
if val < p.data: # 插入值小于p指向节点的值
if p.lchild: # 左孩子节点存在
p = p.lchild # 指针移动至新的节点
else: # 左孩子不存在
p.lchild = BiTreeNode(val) # 插入值
p.lchild.parent = p # 连接父节点
return # 结束循环,返回
elif val > p.data: # 插入值大于p指向节点的值
if p.rchild: # 右孩子存在
p = p.rchild # 指针移动至新节点
else: # 右孩子不存在
p.rchild = BiTreeNode(val) # 插入值
p.rchild.parent = p # 连接父节点
return # 结束循环,返回
else: # val == p.data
return # 不用插入
def query(self, node, val): # 递归写查询
if not node: # 节点不存在
return None # 返回none
elif val > node.data: # 值大于当前节点的值,往右子树找
node = self.query(node.rchild, val) # 变量node是返回的node的赋值
elif val < node.data: # 值小于当前节点的值,往左子树找
node = self.query(node.lchild, val)
else: # val == node.data
node = node # 值相等时返回节点
return node
def query_no_rec(self, val): # 非递归查询
p = self.root # p指针初始指向根节点
while p: # 不是空树
if val < p.data: # 值小于当前节点,往左找
p = p.lchild # p指针下移
elif val > p.data: # 值大于当前节点,往右找
p = p.rchild # p指针往右下移
else: # val == p.data
return p # 退出循环
return None
li = list(range(0,10,2)) # 0-9的偶数
random.shuffle(li)
tree = BST(li) # 创建树
node = tree.root
# print(node.data)
print(tree.query(node, 5)) # 递归
print(tree.query_no_rec(4)) # 非递归输出结果
None
<__main__.BiTreeNode object at 0x00000170A1C1C6A0>4、二叉搜索树:删除
(1)删除操作原理
二叉搜索树的删除与双向链表的删除极为相似。
1)要删除的节点是叶子节点:直接删除。node.parent.lchild 或者 node.parent,rchild = None
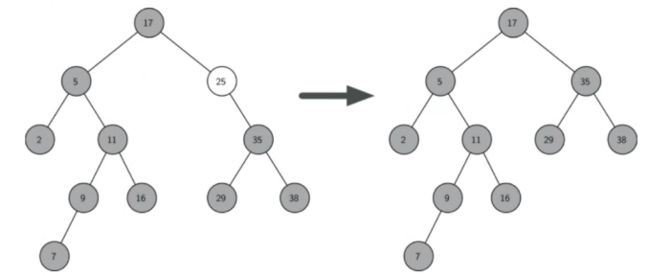
2)要删除的节点只有一个孩子:将此节点的父亲与孩子连接,然后删除该节点。如果删除的节点是根节点,则需要调整子树节点的位置。
3)要删除的节点有两个孩子:将其右子树的值最小的节点(该节点最多有一个右孩子,也可能就是叶子节点),该点一定为右子树的各节点的最后一个左孩子,找到该节点并替换当前节点的值,再删除该接节点
(2)删除操作代码实现
# 二叉搜索树——删除
class BiTreeNode(): # 二叉树节点
def __init__(self, data) -> None: # 属性
self.data = data # 树的值
self.lchild = None # 左孩子
self.rchild = None # 右孩子
self.parent = None # 父节点
# 二叉搜索树 binary search tree
class BST():
def __init__(self, li=None): # 创建树
self.root = None # 根节点为空
# 创建二叉搜索树
if li:
for val in li:
self.insert_no_dec(val) # 循环插入值
def insert_no_dec(self,val): # 非递归插入
p = self.root # 创建指针p,p起始指向根节点
if not p: # p指向节点为空,空树,
self.root = BiTreeNode(val) # 创建根节点
return
while True: # 循环
if val < p.data: # 插入值小于p指向节点的值
if p.lchild: # 左孩子节点存在
p = p.lchild # 指针移动至新的节点
else: # 左孩子不存在
p.lchild = BiTreeNode(val) # 插入值
p.lchild.parent = p # 连接父节点
return # 结束循环,返回
elif val > p.data: # 插入值大于p指向节点的值
if p.rchild: # 右孩子存在
p = p.rchild # 指针移动至新节点
else: # 右孩子不存在
p.rchild = BiTreeNode(val) # 插入值
p.rchild.parent = p # 连接父节点
return # 结束循环,返回
else: # val == p.data
return # 不用插入
def query(self, node, val): # 递归写查询
if not node: # 节点不存在
return None # 返回none
elif val > node.data: # 值大于当前节点的值,往右子树找
node = self.query(node.rchild, val) # 变量node是返回的node的赋值
elif val < node.data: # 值小于当前节点的值,往左子树找
node = self.query(node.lchild, val)
else: # val == node.data
node = node # 值相等时返回节点
return node
def query_no_rec(self, val): # 非递归查询
p = self.root # p指针初始指向根节点
while p: # 不是空树
if val < p.data: # 值小于当前节点,往左找
p = p.lchild # p指针下移
elif val > p.data: # 值大于当前节点,往右找
p = p.rchild # p指针往右下移
else: # val == p.data
return p # 退出循环
return None
# 中序遍历
def in_order(self,root):
if root: # root不为空,递归结束条件
self.in_order(root.lchild) # 访问左孩子
print(root.data, end = ',') # 打印本身
self.in_order(root.rchild) # 访问右孩子
def __remove_node_1(self, node): # 情况1:叶子节点
# 判断是否为根节点
if not node.parent:
self.root = None # 根节点为None,即删除根节点
if node == node.parent.lchild: # node为左孩子
node.parent.lchild = None
else: # node为右孩子
node.parent.rchild = None
def __remove_node_21(self,node): # 情况2.1:只有一个左孩子
if not node.parent: # 根节点
self.root = node.lchild # 根节点为node的左孩子
node.lchild.parent = None # 左孩子的父亲为空
elif node == node.parent.lchild: # node是父亲的左孩子
node.parent.lchild = node.lchild # node父亲的左孩子变为node的左孩子
node.lchild.parent = node.parent # node左孩子的父亲变为node的父亲
else: # node是父亲的右孩子
node.parent.rchild = node.lchild # node父亲的右孩子变为node的左孩子
node.lchild.parent = node.parent # node左孩子的父亲变为node的父亲
def __remove_node_22(self,node): # 情况2.2:只有一个右孩子
if not node.parent: # 根节点
self.root = node.rchild # 根节点为node的右孩子
node.rchild.parent = None # 根节点没有父节点
elif node == node.parent.lchild: # node是父亲的左孩子
node.parent.lchild = node.rchild # node父亲的左孩子变为node的右孩子
node.rchild.parent = node.parent # node右孩子的父亲变为node的父亲
else: # node为父亲的右孩子
node.parent.rchild = node.rchild # node父亲的右孩子变为node的右孩子
node.rchild.parent = node.parent # node右孩子的父亲变为node的父亲
def delete(self,val): # 删除操作(合并)
if self.root: # 不是空树
node = self.query_no_rec(val) # 找到该节点 这步错了
if not node: # node不存在
return False
if not node.lchild and not node.rchild: # 叶子节点
self.__remove_node_1(node) # 情况1
elif not node.rchild: # node只有左孩子
self.__remove_node_21(node) # 情况2.1
elif not node.lchild: # node只有右孩子
self.__remove_node_22(node) # 情况2.2
else: # 情况3 即有左孩子又有右孩子
# 找min_node,右子树的最小节点
min_node = node.rchild # min_node在右子树上
while min_node.lchild: # 直到没有左孩子
min_node = min_node.lchild # min_node一直往左孩子移动,寻找
node.data = min_node.data # 互换两者的值
# 删除min_node
if min_node.rchild: # 只有右孩子
self.__remove_node_22(min_node)
else: # min_node为叶子节点
self.__remove_node_1(min_node)
tree = BST([1,4,2,5,3,8,6,9,7])
tree.in_order(tree.root)
print("")
# 删除值
tree.delete(4)
tree.delete(8)
tree.in_order(tree.root)结果输出
1,2,3,4,5,6,7,8,9,
1,2,3,5,6,7,9,