基于空间平滑MUSIC算法的相干信号DOA估计(2)
空间平滑MUSIC算法(2)
继续上一篇博客,继续讲后向空间平滑和前/后向空间平滑MUSIC算法。
基于空间平滑MUSIC算法的相干信号DOA估计(1)
2.3 后向空间平滑算法
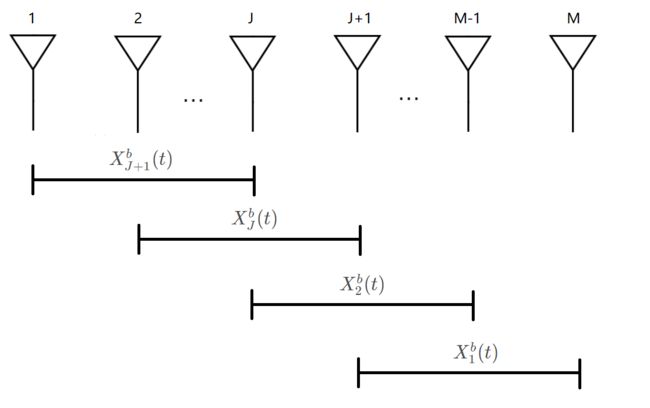
后向空间平滑更准确的说是共轭后向空间平滑,它是对后向子阵列地共轭接收数据协方差矩阵进行平滑。定义第一个共轭后向子阵列由 { M , M − 1 , ⋯ , M − p + 1 } \{M, M-1, \cdots, M-p+1\} {M,M−1,⋯,M−p+1} 组成, 第二个子阵列由 { M − 1 , M − 2 , ⋯ , M − p } \{M-1, M-2, \cdots, M-p\} {M−1,M−2,⋯,M−p} 组成,依次组成的子阵列个数为 L = M − p + 1 个 \mathrm{L}=\mathrm{M}-\mathrm{p}+1 个 L=M−p+1个 。
容易知道,共轭后向空间平滑协方差矩阵 R ~ b \tilde{R}^{b} R~b与前向空间平滑协方差矩阵 R ~ f \tilde{R}^{f} R~f的关系:
R ~ b = J ∗ ( R ~ f ) ∗ ∗ J \tilde{R}^{b}=J*(\tilde{R}^{f})^**J R~b=J∗(R~f)∗∗J利用后向空间平滑协方差矩阵和MUSIC算法也可以分辨出多个相干信号的方位。可以证明,该方法最大也可以检测M/2个相干的信号。
MATLAB代码
% bss.m
% Code For Music Algorithm Based On Backward Spatial Spectrum
% The Signals Are All Coherent
% Author:痒羊羊
% Date:2020/10/29
clc; clear all; close all;
%% -------------------------initialization-------------------------
f = 500; % frequency
c = 1500; % speed sound
lambda = c/f; % wavelength
d = lambda/2; % array element spacing
M = 20; % number of array elements
N = 100; % number of snapshot
K = 6; % number of sources
L = 10; % number of subarray
L_N = M-L+1; % number of array elements in each subarray
coef = [1; exp(1i*pi/6);...
exp(1i*pi/3); exp(1i*pi/2);...
exp(2i*pi/3); exp(1i*2*pi)]; % coherence coefficient, K*1
doa_phi = [-30, 0, 20, 40, 60, 75]; % direction of arrivals
%% generate signal
dd = (0:M-1)'*d; % distance between array elements and reference element
A = exp(-1i*2*pi*dd*sind(doa_phi)/lambda); % manifold array, M*K
S = sqrt(2)\(randn(1,N)+1i*randn(1,N)); % vector of random signal, 1*N
X = A*(coef*S); % received data without noise, M*N
X = awgn(X,10,'measured'); % received data with SNR 10dB
%% reconstruct convariance matrix
%% calculate the covariance matrix of received data and do eigenvalue decomposition
Rxx = X*X'/N; % origin covariance matrix
H = fliplr(eye(M)); % transpose matrix
Rxxb = H*(conj(Rxx))*H;
Rf = zeros(L_N, L_N); % reconstructed covariance matrix
for i = 1:L
Rf = Rf+Rxxb(i:i+L_N-1,i:i+L_N-1);
end
Rf = Rf/L;
[U,V] = eig(Rf); % eigenvalue decomposition
V = diag(V); % vectorize eigenvalue matrix
[V,idx] = sort(V,'descend'); % sort the eigenvalues in descending order
U = U(:,idx); % reset the eigenvector
P = sum(V); % power of received data
P_cum = cumsum(V); % cumsum of V
%% define the noise space
J = find(P_cum/P>=0.95); % or the coefficient is 0.9
J = J(1); % number of principal component
Un = U(:,J+1:end);
%% music for doa; seek the peek
dd1 = (0:L_N-1)'*d;
theta = -90:0.1:90; % steer theta
doa_a = exp(-1i*2*pi*dd1*sind(theta)/lambda); % manifold array for seeking peak
music = abs(diag(1./(doa_a'*(Un*Un')*doa_a))); % the result of each theta
music = 10*log10(music/max(music)); % normalize the result and convert it to dB
%% plot
figure;
plot(theta, music, 'linewidth', 2);
title('Music Algorithm For Doa', 'fontsize', 16);
xlabel('Theta(°)', 'fontsize', 16);
ylabel('Spatial Spectrum(dB)', 'fontsize', 16);
grid on;
可以看到,在6个入射信号均相干的情况下,基于后向空间平滑的MUSIC算法能较好地对其进行DOA估计,且估计精度较高。
2.3 前/后向空间平滑算法
把前向和共轭后向空间平滑协方差矩阵定义为前向空间平滑协方差矩阵和共轭后向空间平滑协方差矩阵的平均值,即:
KaTeX parse error: Unexpected end of input in a macro argument, expected '}' at position 47: …{2}\left(\tilde\̲m̲a̲t̲h̲b̲f̲{R}^{f}+\tilde\…那么只要空间平滑的次数大于等于相干信号源的个数,前向和共轭后向空间平滑协方差矩阵一般情况下都是满秩的。使用前/后向空间平滑的方法最多可以检测的相干信号源个数为 2 M / 3 2 \mathrm{M} / 3 2M/3 个。你可能很好奇这个最大相干信号源检测数是怎么得到的?
假设: 阵列天线的阵元数为 M \mathrm M M个,前/后向空间平滑次数分别为 L \mathrm L L次,则每个子阵的阵元数为 N = M − L + 1 \mathrm N={\mathrm M}-\mathrm{L}+1 N=M−L+1 个, 同时可以知道, 可以分辨的最大信号个数为 M − L \mathrm{M}-\mathrm{L} M−L个, 也就是子阵的阵元个数减 1 ; 1 ; 1;前后向分别平滑 N \mathrm{N} N次可以解相干信号的个数为 2 L 2 \mathrm{L} 2L个, 最大情况下,两者相等所以 M − L = 2 L \mathrm M- \mathrm L=2 \mathrm L M−L=2L,也就是 L = M / 3 ; \mathrm{L}=\mathrm{M} / 3 ; L=M/3; 所以 2 L = 2 M / 3 , 2 \mathrm{L}=2 \mathrm{M} / 3, 2L=2M/3, 所以前/后向空间平滑最大可以解相干的信号个数为 2 M / 3 2 \mathrm{M} / 3 2M/3 个。所以说采用前/后向空间平滑的改进技术可以很大地提高阵列孔径。
MATLAB代码
% fbss.m
% Code For Music Algorithm Based On Forward And Backward Spatial Spectrum
% The Signals Are All Coherent
% Author:痒羊羊
% Date:2020/10/29
clc; clear all; close all;
%% -------------------------initialization-------------------------
f = 500; % frequency
c = 1500; % speed sound
lambda = c/f; % wavelength
d = lambda/2; % array element spacing
M = 20; % number of array elements
N = 100; % number of snapshot
K = 6; % number of sources
L = 10; % number of subarray
L_N = M-L+1; % number of array elements in each subarray
coef = [1; exp(1i*pi/6);...
exp(1i*pi/3); exp(1i*pi/2);...
exp(2i*pi/3); exp(1i*2*pi)]; % coherence coefficient, K*1
doa_phi = [-30, 0, 20, 40, 60, 75]; % direction of arrivals
%% generate signal
dd = (0:M-1)'*d; % distance between array elements and reference element
A = exp(-1i*2*pi*dd*sind(doa_phi)/lambda); % manifold array, M*K
S = sqrt(2)\(randn(1,N)+1i*randn(1,N)); % vector of random signal, 1*N
X = A*(coef*S); % received data without noise, M*N
X = awgn(X,10,'measured'); % received data with SNR 10dB
%% reconstruct convariance matrix
%% calculate the covariance matrix of received data and do eigenvalue decomposition
Rxx = X*X'/N; % origin covariance matrix
H = fliplr(eye(M)); % transpose matrix
Rxxb = H*(conj(Rxx))*H;
Rxxfb = (Rxx+Rxxb)/2;
Rf = zeros(L_N, L_N); % reconstructed covariance matrix
for i = 1:L
Rf = Rf+Rxxfb(i:i+L_N-1,i:i+L_N-1);
end
Rf = Rf/L;
[U,V] = eig(Rf); % eigenvalue decomposition
V = diag(V); % vectorize eigenvalue matrix
[V,idx] = sort(V,'descend'); % sort the eigenvalues in descending order
U = U(:,idx); % reset the eigenvector
P = sum(V); % power of received data
P_cum = cumsum(V); % cumsum of V
%% define the noise space
J = find(P_cum/P>=0.95); % or the coefficient is 0.9
J = J(1); % number of principal component
Un = U(:,J+1:end);
%% music for doa; seek the peek
dd1 = (0:L_N-1)'*d;
theta = -90:0.1:90; % steer theta
doa_a = exp(-1i*2*pi*dd1*sind(theta)/lambda); % manifold array for seeking peak
music = abs(diag(1./(doa_a'*(Un*Un')*doa_a))); % the result of each theta
music = 10*log10(music/max(music)); % normalize the result and convert it to dB
%% plot
figure;
plot(theta, music, 'linewidth', 2);
title('Music Algorithm For Doa', 'fontsize', 16);
xlabel('Theta(°)', 'fontsize', 16);
ylabel('Spatial Spectrum(dB)', 'fontsize', 16);
grid on;
因为前/后向空间平滑的改进技术很大地提高了阵列孔径,从以上的DOA结果图可以看出分辨率提高了。
参考论文:《阵列信号处理相关技术研究,陈四根》
代码Code均为原创。
欢迎转载,表明出处。