深度学习-损失、优化器
目录
- 0.损失函数
-
- 0.0 回归损失函数
-
- 0.0.1 L1 Loss
- 0.0.2 L2 Loss
- 0.0.3 Smooth L1 Loss
- 0.1 分类损失
-
- 0.1.0 cross entropy
- 0.1.1 Focal loss
- 1.优化器
-
- 1.1 SGD
- 1.2 RMSprop
- 参考:
0.损失函数
0.0 回归损失函数
0.0.1 L1 Loss
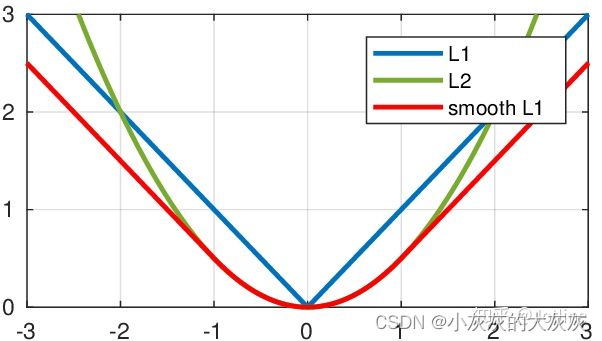
L1的loss可以用函数表示为,挺好的,就是0点不可导
L ( x , y ) = 1 n ∑ i = 1 n ∣ y i − f ( x i ) ∣ L(x,y)=\frac{1}{n}\sum_{i=1}^n|y_i-f(x_i)| L(x,y)=n1i=1∑n∣yi−f(xi)∣
0.0.2 L2 Loss
L2的loss可以用汉书表示为,0点可导,但远处容易梯度爆炸
L ( x , y ) = 1 n ∑ i = 1 n ( y i − f ( x i ) ) 2 L(x,y)=\frac{1}{n}\sum_{i=1}^n(y_i-f(x_i))^2 L(x,y)=n1i=1∑n(yi−f(xi))2
0.0.3 Smooth L1 Loss
L1的Smooth loss可以用汉书表示为,挺好的,结合了L1、L2的优点
L ( x , y ) = 1 n ∑ i = 1 n { 1 2 ( y i − f ( x i ) ) 2 , i f ∣ y i − f ( x i ) ∣ ≤ 1 ∣ y i − f ( x i ) ∣ − 1 2 , o t h e r w i s e L(x,y)=\frac{1}{n}\sum_{i=1}^n \begin{cases} \frac{1}{2}(y_i-f(x_i))^2\ \ ,\quad if \ |y_i-f(x_i)| \leq 1\\ |y_i-f(x_i)|-\frac{1}{2}, \quad otherwise \end{cases} L(x,y)=n1i=1∑n{21(yi−f(xi))2 ,if ∣yi−f(xi)∣≤1∣yi−f(xi)∣−21,otherwise
0.1 分类损失
0.1.0 cross entropy
正确分类的就不计算损失,计算错误的要计算损失
N个样本,每个样本有M个类别需要预测
L = 1 N ∑ i = 1 N L ( y i , p i ) = 1 N ∑ i = 1 N ∑ j = 1 M y i c l n ( p i c ) L = \frac{1}{N}\sum_{i=1}^NL(y_i, p_i) = \frac{1}{N}\sum_{i=1}^N\sum_{j=1}^My_{ic}ln(p_{ic}) L=N1i=1∑NL(yi,pi)=N1i=1∑Nj=1∑Myicln(pic)
N N N 表示样本总数目
M M M 表示单个样本中的类别数目
y i c y_{ic} yic 表示 i i i 样本中,第 c c c 个目标是否正确分类,正确时值为 0 0 0 否则为 1 1 1
p i c p_{ic} pic 表示 i i i 样本中,第 c c c 个目标的预测概率, 值为 0 ~ 1
0.1.1 Focal loss
上面已经得出交叉熵损失是所有样本中损失的均值,但是如果样本中正负样本的分布不均匀
1.优化器
优化器的最终目标是最小化Loss函数,从而优化网络本身参数
它包含了 learning rate 和 函数两部分
Momentum-动量法
1.1 SGD
又名随机梯度下降,前期算法没有增加动量,目前是一类动量法
优化参数的过程可以表示为如下,其中 α \alpha α 就是学习率, ν \nu ν 是动量, 参数 γ \gamma γ通常取值0.9
θ t = θ t − 1 − ν t ν t = γ ν t − 1 + α ∂ L ( θ ) ∂ θ \theta_t = \theta_{t-1}-\nu_t \\ \nu_t=\gamma \nu_{t-1} + \alpha \frac{\partial L(\theta)}{\partial\theta} θt=θt−1−νtνt=γνt−1+α∂θ∂L(θ)
代表着当前如何走与梯度有关,还与过去的累积梯度有关
1.2 RMSprop
此文仅供学习使用,禁止其他用处
参考:
CSDN:深度学习中常见的损失函数(L1Loss、L2loss)
知乎:如何通俗理解深度学习优化器?
博客园:深度学习中常用的优化器简介
知乎:从 SGD 到 Adam —— 深度学习优化算法概览(一)
知乎:损失函数|交叉熵损失函数