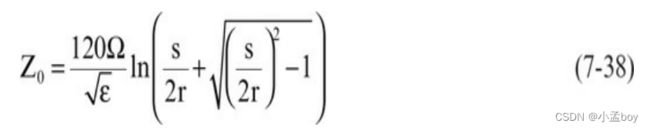传输线的物理基础（八）：用近似值和二维场计算特性阻抗

设计一个特定的目标特性阻抗实际上是调整线宽、电介质厚度和介电常数的问题。如果我们知道传输线的长度和导体周围材料的介电常数，并且我们可以计算出特征阻抗，我们就可以使用上面的关系来计算所有其他参数。

当然，每一种不同类型的横截面几何形状都会有不同的几何特征与特征阻抗之间的关系。通常，我们可以使用三种类型的分析来从几何形状计算特征阻抗：1. 经验法则 2. 近似值 3. 二维场求解器.

两个最重要的经验法则与使用 FR4 制造的微带线和带状线的特性阻抗有关。 50 欧姆传输线的横截面如下图。

FR4 中 50 欧姆传输线的比例横截面。左图：w = 2 × h 的 50 欧姆微带线。右图：b = 2 × w 的 50 欧姆带状线。

 根据经验，FR4 中的 50 欧姆微带线的线宽是电介质厚度的两倍。 50 欧姆带状线的平面之间的总电介质间距等于线宽的两倍。

只有三种横截面几何形状具有精确的方程式：同轴、双圆线和圆线平面几何形状（见图 7-31）。所有其他都是近似值。同轴电缆的特性阻抗和几何形状之间的关系是：

只有三个横截面的特性阻抗有精确的方程。所有其他都是近似值。

 对于双平行圆线，特性阻抗为：

 对于平面上的圆棒，特性阻抗为：

 其中：
Z = 特性阻抗，以欧姆为单位
a = 同轴电缆的内半径，以英寸为单位
b = 同轴电缆的外半径，以英寸为单位
r = 圆杆的半径，以英寸为单位
s = 圆杆的中心间距，以英寸为单位
h = 杆中心在平面上的高度，以英寸为单位
ε = 材料的介电常数

这些关系假设介电材料完全均匀地填充所有存在电场的空间。如果不是这种情况，则影响信号沿导体传输速度的有效介电常数将是电介质混合物的某种复杂组合。这通常只能使用场解算器来计算。

除了极少数例外，几乎所有其他用于将特性阻抗与几何形状相关联的方程式都是近似值。当偏离超过 5% 可能会过度增加设计时间和成本时，不应将近似值用于传输线设计的最终签核。当精度很重要时，应使用经过验证的 2D 场解算器。

近似值的价值在于它们显示了几何项之间的关系，并可用于电子表格中的敏感性分析。 IPC 推荐的最流行的微带线近似值是：

 对于带状线，IPC 推荐的近似值是：

 其中：
Z = 特性阻抗，以欧姆为单位
h = 信号迹线下方的电介质厚度
平面，以密耳为单位
w = 线宽，以密耳为单位
b = 平面间距，以密耳为单位
t = 金属厚度，以密耳为单位
ε = 介电常数

如果我们忽略走线厚度 t 的影响，则两种结构的特征阻抗仅取决于电介质厚度与线宽的比率。这是一个非常重要的关系。

首先，带状线和微带线的特性阻抗将与电介质厚度与线宽之比成比例。只要这个比率恒定，特性阻抗就会恒定。

例如，如果线宽加倍并且电介质间距加倍，则作为一阶近似值的特性阻抗将保持不变。尽管这些方程式看起来很复杂，但这并不能衡量它们的准确性。了解近似精度的唯一方法是将其与经过验证的场求解器的结果进行比较。

用二维场求解器计算特性阻抗

所有2D场解算器所做的基本假设是，几何体沿着直线的长度是均匀的。也就是说，当我们沿着传输线的长度向下移动时，横截面几何形状保持不变。这是控制阻抗线的基本定义，即横截面是均匀的。在这种情况下，只有一个特征阻抗来描述线路。这就是为什么2D场求解器是提供均匀传输线特性阻抗的精确预测的正确工具。只有2D横截面信息是重要的。

只要精度很重要，就应该使用 2D 场解算器。这意味着在签署设计并提交硬件之前，应使用 2D 场求解器设计叠层。有时有人争论说，如果制造公差是 10%，即使预测准确度是 5%，我们也不应该在意。
通过使用 2D 场解算器，可以计算微带线的特性阻抗。将这些结果与基于 IPC 近似值的预测进行比较。图 7-32 显示了随着线宽的变化，介电常数为 4、铜为 1/2 盎司、电介质厚度为 10 密耳的微带线的预测特征阻抗。在 50 欧姆附近和以上，一致性非常好。然而，对于较低的阻抗，IPC 近似值可能会偏离 25%。

具有10密耳厚FR4电介质和1/2盎司铜的微带的场解算器结果（圆）和IPC近似值（线）的比较。Ansoft 2D提取器的场解算器结果。

 对带状线进行了相同的比较，如图7-33所示。接近50欧姆的一致性非常好，但对于低阻抗，近似值可能会偏离25%以上。当精度很重要时，不应使用近似值。

具有10密耳厚FR4电介质和1/2盎司铜的带状线的场解算器结果（圆圈）和IPC近似值（线）的比较。Ansoft 2D提取器的场解算器结果。

 除了提供特性阻抗的精确估计外，2D场解算器还可以深入了解二阶效应的影响，例如：
•返回路径的宽度
•信号迹线导体的厚度
•表面痕迹上存在焊料掩模
•有效介电常数

返回路径的宽度如何影响特性阻抗？应用Bogatin规则9的原理，我们可以预测，如果返回路径的宽度很窄，电容应该更小，特性阻抗应该更高。使用场解算器，我们可以计算返回路径的宽度，这样就不再重要了。

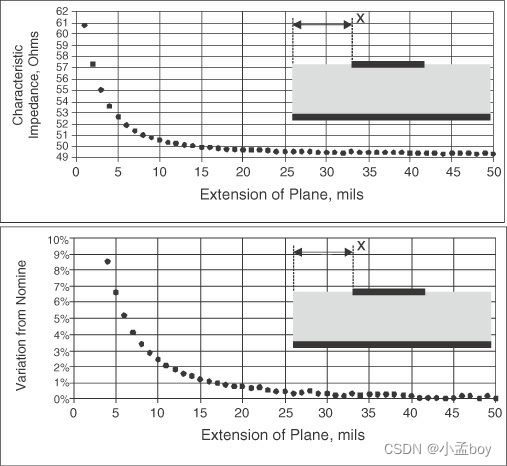
该图显示了介电常数为 4、迹线厚度为 0.7 mil 的微带线的计算特性阻抗，对应于 1/2 盎司铜、5 mil 的电介质厚度和 10 mil 的线宽。这名义上是一条 50 欧姆的线路。改变返回路径的宽度并计算特征阻抗。如果信号迹线每侧的延伸宽度大于 15 密耳，则特性阻抗与其无限宽度值的偏差小于 1%。因为沿着迹线边缘的边缘场与电介质厚度成比例，所以这是重要的比例因子。信号路径任一侧的返回路径范围应大致为电介质厚度 h 的三倍。

顶部：随着返回路径平面的加宽，具有10密耳宽迹线和5密耳厚电介质的微带的计算特性阻抗。底部：与标称值的变化。Ansoft 2D提取器的场解算器结果。

根据粗略的经验，当返回路径无限宽时，返回路径应至少延伸信号走线任一侧的电介质厚度的三倍，以使特征阻抗不超过该值的 1%.

再次遵循规则 9，我们预计随着走线厚度的增加，侧面会出现更多的边缘场，并且单位长度的电容会增加。这将使特性阻抗随着导体厚度的增加而降低。使用 2D 场求解器，我们可以计算走线厚度从 0.1 密耳厚变为 3 密耳厚时的特性阻抗。如下图所示。曲线上的每个点都是针对不同走线厚度计算出的特性阻抗。果然，随着金属厚度的增加，边缘场电容增加，特性阻抗降低。较厚的金属意味着信号走线和返回路径之间的电容较高，这也意味着较低的特性阻抗。但是，正如我们从计算结果中看到的那样，这并不是一个很大的影响；这是二阶的。 

随着走线厚度的变化，标称50欧姆微带的计算特性阻抗。圆圈是计算结果；线路为2欧姆/密耳。Ansoft 2D提取器的场解算器结果。

 作为粗略的经验法则，特性阻抗的减小是信号走线厚度的每密耳大约2欧姆。

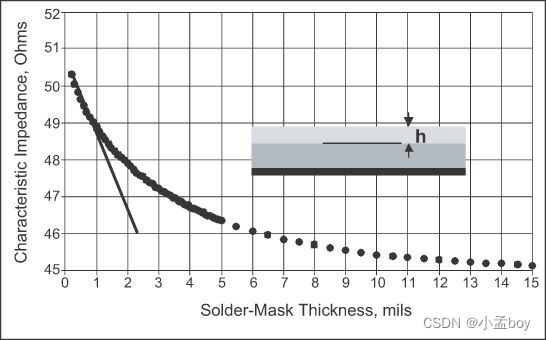
如果微带顶部有一层薄的阻焊层，则边缘场电容会增加，特性阻抗会降低。对于与上述相同的微带，但使用仅0.1密耳厚的导体，使用介电常数4计算增加的焊料掩模涂层的特性阻抗。下图显示了特性阻抗的下降。对于薄涂层来说，它大约是2欧姆/密耳的涂层。在大约10密耳厚的涂层之后，特性阻抗不再受到影响，因为所有外部边缘场都包含在涂层的前10密耳中。这是对边缘场在表面上方延伸多远的测量。

添加了作为介电常数为 4 的阻焊层的标称 50 欧姆微带线的计算特性阻抗。圆圈是场解算器的结果；该线是 2 欧姆/密尔。 Field solver结果来自Ansoft 2D Extractor。

 当然，阻焊层通常为 0.5 mil 到 2 mils。在这种情况下，我们看到阻焊层的存在可以将特性阻抗降低多达 2 欧姆——这是一个很大的数量。使用阻焊层达到目标阻抗需要线宽比标称值窄，因此阻焊层会将阻抗降低到目标值。

最后一个示例说明特性阻抗取决于微带线中走线上方的介电分布。当然，在带状线中，所有场都包含在电介质中，因此上平面顶部的阻焊层对特性阻抗没有影响。除了受不均匀介电分布影响的特性阻抗外，场所经历的有效介电常数也受介电分布影响。在微带线中，决定信号速度的有效介电常数取决于电介质的特定几何形状。通常，有效介电常数只能使用场解算器来准确计算。