实验二 图像空间域&频率域滤波

一．实验目的：

1. 模板运算是空间域图象增强的方法，也叫模板卷积。

（1）平滑：平滑的目的是模糊和消除噪声。平滑是用低通滤波器来完成，在空域中全是正值。

（2）锐化：锐化的目的是增强被模糊的细节。锐化是用高通滤波器来完成，在空域中，接近原点处为正，在远离原点处为负。

2．掌握二维快速傅里叶变换（FFT）的实现，对频谱图像可视化操作。

3．了解频域滤波的内容，学会如何在频域中直接生成滤波器，包括平滑频域滤波器——低通滤波器、锐化频域滤波器——高通滤波器，并利用生成的滤波器对输入图像进行频域处理。

4．掌握绘制三维可视化滤波器图形的方法。

二．实验内容：

（1）利用线性空间滤波（均值滤波）对一幅图象进行平滑，验证模板尺寸和滤波参数对图象的模糊效果的影响。

（2）利用非线性空间滤波器（中值滤波）对一幅噪声图象（椒盐噪声）进行平滑去噪，同时检验两种滤波模板（分别使用一个5×5的线性邻域平均模板和一个非线性模板：3×3中值滤波器）对噪声的滤波效果。

（3）利用线性空间滤波器，对灰度图象分别利用二阶标准Laplacian算子和对角线Laplacian算子对其进行锐化操作，增强图像边缘，验证检测效果。

（4）实现二维快速傅里叶变换，以图像形式显示傅里叶频谱。

（5）利用已给出的自定义的M函数，建立频域滤波器的传递函数H(u, v)

（6）绘制滤波器传递函数H(u, v)三维图形，并以图像形式显示滤波器。

（7）对输入图像进行频域滤波处理。

三．实验原理：

1．线性空间滤波

函数imfilter来实现线性空间滤波，语法为：

            g = imfilter(f, w, filtering_mode, boundary_options, size_options)

其中，f是输入图像，w为滤波模板，g为滤波结果

filtering_mode用于指定在滤波过程中是使用相关运算(‘corr’)还是卷积运算(‘conv’)，相关就是按模板在图像上逐步移动运算的过程，卷积则是先将模板旋转180度，再在图像上逐步移动的过程，显然，若模板中心对称，则相关和卷积运算是相同操作，默认为相关运算；

boundary_options用于处理边界充零问题，默认为赋零，若该参数为’replicate’表示输出图像边界通过复制原图像边界的值来扩展；

size_options可以是’full’或’same’，默认为’same’，表示输出图像与输入图像的大小相同。

 

均值滤波：

>>w = ones(31)/(31*31)  %建立一个31×31大小的均值滤波器

>>g1 = imfilter(f, w)  %相关运算，默认边界充零

>>imshow(g1)

>>g2 = imfilter(f, w, ‘replicate’)  

>>figure, imshow(g2)

实验报告

1．用31×31均值滤波模板，并分别采用参数boundary_options默认值和‘replicate’对图像test_pattern进行平滑处理，观察不同参数对滤波效果的影响。；

用3×3，5×5，7×7均值滤波模板对图像lena平滑处理，观察不同模板尺寸对滤波效果的影响。

2．非线性滤波器

数字图像处理中最著名的统计排序滤波器是中值滤波器，MATLAB工具箱提供了二维中值滤波函数medfilt2，语法为：

        g = medfilt2(f, [m n], padopt)

矩阵[m n]定义了一个大小为m×n的邻域，中值就在该邻域上计算；而参数padopt指定了三个可能的边界填充选项：’zeros’（默认值，赋零），’symmetric’按照镜像反射方式对称地沿延其边界扩展，’indexed’，若f是double类图像，则以1来填充图像，否则以0来填充图像。

该函数的默认形式为：

        g = medfilt2(f)

它默认使用一个大小为3×3的邻域来计算中值，并用0来填充图像的边界。

>>fn = imnoise(g, ‘salt & pepper’, 0.2)

 %对图像f加入椒盐噪声，其中黑点和白%点出现的概率为0.2

>>imshow(fn)

>>gm = medfilt2(fn)  %默认中值滤波

>>figure, imshow(gm)

>>gms = medfilt2(fn, ‘symmetric’)%按照镜像反射方式对称地沿延其边界扩展

>> figure, imshow(gms)

实验报告

2. 用3×3，5×5，7×7邻域大小的中值滤波对椒盐噪声污染的图像board进行去噪平滑处理。观察不同邻域大小对中值滤波效果的影响。

3．线性空间滤波器

MATLAB工具箱支持一些预定义的二维线性空间滤波器，这些空间滤波器可通过函数fspecial实现。生成滤波模板的函数fspecial的语法为：

        w = fspecial(‘type’, parameters)

其中，’type’表示滤波器类型，parameters进一步定义了指定的滤波器。

fspecial(‘laplacian’, alpha) 一个大小为3×3的拉普拉斯滤波器，其形状由alpha指定，alpha是范围[0, 1]的数。alpha默认为0.5。实现了一个常见的拉普拉斯算子模板：，若alpha = 0，则为标准拉普拉斯模板，另一个考虑对角线元素的拉普拉斯模板是。

 

>>w4 = fspecial(‘laplacian’, 0)  %建立一个标准拉普拉斯模板

>>w8 = [1 1 1; 1 -8 1; 1 1 1]  %手工指定滤波器，建立一个对角线拉普拉斯

%模板

>>g4 = imfilter(f, w4, ‘replicate’)

>>figure, imshow(g4)

>>g4g = f – g4

>>figure, imshow(g4g)

>>g8 = imfilter(f, w8, ‘replicate’)

>>figure, imshow(g8)

>>g8g = f – g8

>>figure, imshow(g8g)

实验报告

3. 分别用标准拉普拉斯模板和对角线拉普拉斯模板对图像moon进行边缘增强，并与原图像叠加运算，观察并对比增强后的效果。

4．快速傅里叶变换FFT的实现

   一个大小为M×N的图像矩阵f的快速傅里叶变换FFT可以通过MATLAB函数fft获得，其简单语法：

                       F = fft2(f)

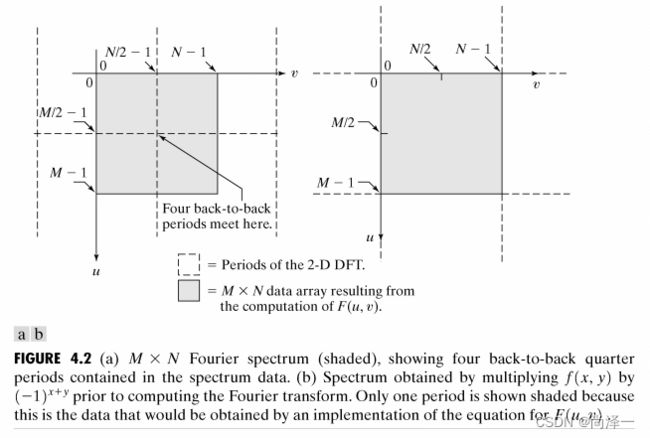
   该函数返回一个大小仍为M×N的傅里叶变换，数据排列如图4.2(a)所示；即数据的原点在左上角，而四个四分之一周期交汇于频率矩形的中心。

 

函数fftshift将变换的原点移动到频率矩形的中心，语法为：

             Fc = fftshift(F)

F是用fft2得到的傅里叶变换，即图4.2(a)，而Fc是已居中的变换，即图4.2(b)。

傅里叶频谱可以使用函数abs来获得，语法为：

                    S = abs(F)

该函数计算数组的每一个元素的幅度，也就是实部和虚部平方和的平方根，即若某个元素为F = a +bj，则。

 

通过显示频谱的图像进行可视化分析是频域处理的一个重要方面。

例如，对图4.3(a)所示的图像f (image.bmp)我们计算它的傅里叶变换并显示其频谱：

>> F = fft2(f)

>> S = abs(F)

>> figure,imshow(S, [ ])

请尝试直接显示F和S，并做比较

图4.3(b)显示了结果，图像四个角上的亮点就是四个四分之一周期的中心点。

键入命令：

>> Fc = fftshift(F)

>> Sc = abs(Fc)

>>figure, imshow(Sc, [ ])

将产生图4.3(c)所示的图像，居中后的结果在该图像中是很明显的。

虽然该移动像我们期望的那样完成了，但该频谱中Sc值的动态范围很大(0到204000)与8比特显示相比要大的多，使用对数变换来处理，命令：

>> ScL = log(1 + Sc)

>> figure, imshow(ScL, [ ])

产生如图4.3(d)所示的结果。

 

实验报告

4. 对图像image2.bmp, image3.bmp（二选一）和house（四选一）进行傅里叶变换

5．在频率域中直接生成滤波器

低通滤波器传递函数Hlp(u, v)：

高斯低通滤波器：

 

高通滤波器传递函数Hhp(u, v)：

            Hhp(u, v) = 1 - Hlp(u, v)

直接利用函数fspecial建立低通滤波器的传递函数，语法为H=fspecial(type)：

>> help fspecial

 fspecial Create predefined 2-D filters.

    H = fspecial(TYPE) creates a two-dimensional filter H of the

    specified type. Possible values for TYPE are:

      'average'   averaging filter

      'disk'      circular averaging filter

      'gaussian'  Gaussian lowpass filter

      'laplacian' filter approximating the 2-D Laplacian operator

      'log'       Laplacian of Gaussian filter

      'motion'    motion filter

      'prewitt'   Prewitt horizontal edge-emphasizing filter

      'sobel'     Sobel horizontal edge-emphasizing filter

    Depending on TYPE, fspecial may take additional parameters

    which you can supply.  These parameters all have default

    values.

  

    H = fspecial('gaussian',HSIZE,SIGMA) returns a rotationally

    symmetric Gaussian lowpass filter of size HSIZE with standard

    deviation SIGMA (positive). HSIZE can be a vector specifying the

    number of rows and columns in H or a scalar, in which case H is a

    square matrix.

    The default HSIZE is [3 3], the default SIGMA is 0.5.

    H = fspecial('laplacian',ALPHA) returns a 3-by-3 filter

    approximating the shape of the two-dimensional Laplacian

    operator. The parameter ALPHA controls the shape of the

    Laplacian and must be in the range 0.0 to 1.0.

    The default ALPHA is 0.2.

H=fspecial(type, HSIZE, SIGMA), 默认[3 3],0.5

H = fspecial('laplacian', ALPHA) 默认0.2，范围为0.0-1.0

例：

H1 = fspecial('gaussian’,[500 500],50) %建立一个高斯低通滤波器，截止频率50

H2 = fspecial('laplacian’，0.5)

思考：

fspecial建立的是低通还是高通滤波器？对应的高通或低通应该怎么建立？

fspecial可以建立各种类型的滤波器，包括低通、高通、带通、带阻等。通过指定不同的参数，可以创建不同类型的滤波器。

如果需要建立低通滤波器，可以使用fspecial('gaussian', hsize, sigma)，其中hsize为滤波器大小，sigma为标准差。

如果需要建立高通滤波器，可以使用fspecial('laplacian', alpha)，其中alpha为滤波器的系数。

需要根据具体应用场景和需求选择合适的滤波器类型和参数。

绘制滤波器传递函数H(u, v)三维图形，并以图像形式显示滤波器

对二维滤波器函数的传递函数进行可视化，使用函数mesh，语法为：

              mesh(H)  %默认是彩色绘图

该函数将绘制一个x = 1:M和y = 1:N的线框图，其中[M N] = size(H)。

若M和N很大，则线框图的密度会大到不可接受，将以连续曲面显示。在这种情况下，我们可以使用语法：

               mesh(H(1:k:end, 1:k:end))

经验表明，沿每个轴40到60个等分可在外观和分辨率上有较好的平衡。

例：

>> mesh(H1)  %滤波器的三维透视图

>> figure, mesh(H1(1:10:500, 1:10:500))

>> axis([0 50 0 50 0 1])

>> figure, imshow(H1)  %以图像形式显示滤波器

>> GLPFc = fftshift(H1)  %频率矩形中心化

>> mesh(GLPFc)  

>> figure, mesh(GLPFc(1:10:500, 1:10:500))

>> axis([0 50 0 50 0 1])

>> figure, imshow(GLPFc)  

实验报告

5. 生成高斯低通滤波器和高通滤波器，绘制其三维透视图；生成拉普拉斯滤波器，并尝试绘制其三维透视图。

6．对输入图像进行频域滤波处理

使用imfilter，语法为： 

g = imfilter(f, w, filtering_mode, boundary_options, size_options)

 f是输入的空间域图像，w是频率域滤波器，g是经频域滤波后的输出图像

实验报告

6. 针对lena或test_pattern，用gaussian、laplacian分别进行滤波，设置不同滤波器大小和截止频率，比较滤波图像外观。