常见排序算法

目录

一、插入排序

1、直接插入排序

2、希尔排序(缩小增量插入排序）

二、选择排序

三、堆排序

四、冒泡排序

五、快速排序（递归）

1、交换法

2、挖坑法

3、前后指针法（推荐）

4、快排再优化

六、快速排序（非递归）

七、归并排序

1、递归版

2、非递归版（改循环）

八、计数排序

---

一、插入排序

1、直接插入排序

时间复杂度：

最坏：O（N^2）

最好：O(N)

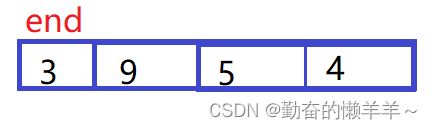
思路：我们打牌时整牌的过程其实用的就是插入排序的思想。

如：3 9 5 4 排升序

除了第一个数3外，剩下的数都可以看成依次插入的数。

当插入9时，end指针指向3，3<9，9就放在end的下一个位置。

接着插入5,end指向9，9>5,end往前走指向3，3<5, 5就放在end（3）的下一个位置。

再继续插入4，end指向5，5>4，end往前走指向9,

9>4,end往前走指向3,3<4,4就放在end（3）的下一个位置。

void InsertSort(int* a, int n)
{
	for (int i = 1; i < n; i++)
	{
		int tmp = a[i];
		int end = i - 1;
		while (end >= 0)
		{
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;
			}
		}
		a[end + 1] = tmp;
	}
}

2、希尔排序(缩小增量插入排序）

时间复杂度：O(N^1.3)大致可理解为nlogn
思路：

 1) 预排序（使数组接近有序）

 2）直接插入排序

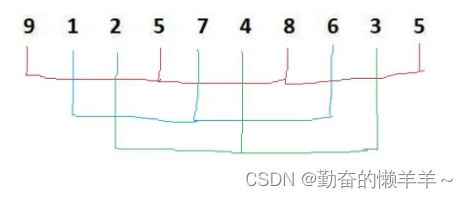
分组进行插入排序，间隔为gap的分一组：

假设gap=3

void shellSort(int*a,int n)
{
	int gap = 3;
	for (int i = 0; i < n - gap; i++)
	{
		int end = i;
		int tmp = a[end + gap];
		while (end>=0)
		{
			if (tmp < a[end])
			{
				a[end + gap] = a[end];
				a[end] = tmp;
				end -= gap;
			}
			else
			{
				break;
			}
		}
		a[end + gap] = tmp;
	}
}

gap为多少合适呢？

gap越大，跳得越快，越无序

gap越小，跳得越慢，越有序

可以这样：

让gap=n，gap/=2

也可以gap/=3+1（最后gap一定会变为1）

参考代码：

void shellSort(int*a,int n)
{

	int gap = n;
	while (gap>1)
	{
		gap/= 2;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					a[end] = tmp;
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

二、选择排序

时间复杂度：O（N^2）

思路：选出最大最小的数放两端

//选择排序
void SelectSort(int*a,int n)
{
	int left = 0, right = n - 1;
	while (left a[maxi])
			{
				maxi = i;
			}
			if (a[i] < a[mini])
			{
				mini = i;
			}
		}
		swap(&a[left], &a[mini]);
		if (left==maxi) 
		{
			maxi = mini;
		}
		swap(&a[right], &a[maxi]);
		left++;
		right--;
	}
}

三、堆排序

参考之前的博文：https://blog.csdn.net/m0_73065213/article/details/129733076?spm=1001.2014.3001.5501

四、冒泡排序

时间复杂度：

最坏：O(N^2)

最好O(N)

前面有写博客专门讲过，详细讲解参考之前的博文。

void BubbleSort(int* a, int n)
{
	int j = 0, i = 0;
	for (i = 0; i < n-1; i++)//n个数只要调n-1躺
	{
		for (j = 0; j < n - 1-i; j++)//一趟比几次
		{
			if (a[j] > a[j + 1])
			{
				swap(&a[j], &a[j + 1]);
			}
		}
	}
}

五、快速排序（递归）

时间复杂度：O（N*logN）

基本思想：任取待排序元素中的某元素作为基准值，按照该排序码将待排序列分割成两个子序列，左子序列中所有元素均小于等于基准值，右子序列所有元素均大于等于基准值，然后左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

1、交换法

步骤：

1、确定一个基准值key

2、调位置

        左右两个指针，左找大，右找小，找到后交换位置。

        让左边小于等于基准值，让右边大于等于基准值。

3、递归调左右子序列

void QuickSort(int*a,int left,int right)
{
	int begin = left, end = right;
	//递归返回条件
	//left是可能大于right
	if (left >= right)return;
	
	int keyi = left;
	while (left < right)
	{
		//坑1：内层两个循环一定要判断left= a[keyi])
			right--;
		while (left

按照上面的写法，keyi取left的话，若序列原本就有序，效率就会变成N^2。

因此，为了优化这个问题，下面介绍两种方法：

方法一：随机选keyi

void QuickSort(int*a,int left,int right)
{
	//递归返回条件
	//left是可能大于right
	if (left >= right)return;

	int begin = left, end = right;
	int randi = left+(rand() % (right - left));
	Swap(&a[left], &a[randi]);
	int keyi = left;
	while (left < right)
	{
		//坑1：一定要判断left= a[keyi])
			right--;
		while (left

方法二：三数取中

用前中后三个数中不是最大也不是最小的数做keyi。

	//三数取中
	int midi = GetMidNumi(a, left, right);
	Swap(&a[left], &a[midi]);
	int keyi = left;

int GetMidNumi(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[left] < a[mid])
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[left] > a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else
	{
		if (a[mid] > right)
		{
			return mid;
		}
		else if (a[right] < a[left])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
}

为什么相遇位置一定比keyi小？

☆左边做keyi，右边先走时，相遇位置一定比keyi小

☆右边做keyi，左边先走时，相遇位置一定比keyi大

相遇可能的几种情况：

1、right找到小，left还没找到就相遇了，所以相遇位置一定比keyi小。

2、right找小，没找到，就跟left相遇了，相遇的位置是上一轮交换的数字或者left还在原地，也是比keyi小的或者相等。

2、挖坑法

这种方法是把left位置的值用key保存，然后right找到大的值放left位置，再将left找到的小的值放right位置。

下面是单趟的代码：

	int key = a[left];
	int hole = left;
	while (leftkey)
			right--;
		a[hole] = a[right];
		hole = right;
		while (left < right && a[left] < key)
			left++;
		a[hole] = a[left];
		hole = left;
	}
	a[hole] = key;

3、前后指针法（推荐）

void QuickSort3(int* a, int left, int right)
{
	if (left >= right)return;
	int begin = left, end = right;
	int midi = GetMidNumi(a, left, right);
	Swap(&a[left], &a[midi]);
	int keyi = left;
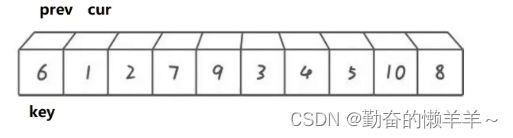
	int prev = left;
	int cur = prev + 1;
	while (cur <= right)
	{
		if (a[cur] < a[keyi] && ++prev != cur)//如果a[cur]>key,prev就不会++
			Swap(&a[cur], &a[prev]);
		cur++;
	}
	Swap(&a[prev], &a[keyi]);
	keyi = prev;
	QuickSort3(a, begin, keyi - 1);
	QuickSort3(a, keyi + 1, end);
}

4、快排再优化

数据量很小时，用快排其实是很麻烦的，因此，当快排递归到最后几层时，递归的区间很小，我们可以选择用插入排序，这样快排的效率就大大优化了。

	if ((right - left + 1) > 10)
	{
		QuickSort3(a, left, right);
	}
	else
	{
		InsertSort(a + left, right - left + 1);
	}

此外，当数据重复较多时，快排效率也会大大降低，此时可以用三路划分的方法进行优化

六、快速排序（非递归）

前面我们都是用递归将区间不断的分小，

非递归的快排是用栈模拟递归将区间不断划分的过程。

如a[5]={2,1,4,3,5}

数组下标范围是0-4，我们先让4入栈，再让0入栈（因为栈的先进后出原则）

第一轮while：

取出栈中区间0-4，进行一轮排序后，得到>keyi的区间和

对于此例，此时keyi为3，keyi+1=4=end所以大于keyi的区间不存在；

keyi-1=2>0,区间存在，让0-2入栈。

第二轮while：

取出栈中区间0-2，进行一轮排序后，得到>keyi的区间和

keyi=1，keyi+1=end,keyi-1=begin,所以区间不存在，不入数据

此时，栈为空，循环结束。

void QuickSortNonR(int* a, int left, int right)
{
	Stack st;
	StackInit(&st);
	StackPush(&st, right);
	StackPush(&st, left);
	while (!isEmpty(&st))
	{
		int begin = StackTop(&st);
		StackPop(&st);
		int end = StackTop(&st);
		StackPop(&st);
		int keyi = PartSort3(a, begin, end);
		if (keyi + 1 < end)
		{
			StackPush(&st, end);
			StackPush(&st, keyi + 1);
		}
		if (keyi - 1 > begin)
		{
			StackPush(&st, keyi - 1);
			StackPush(&st, begin);
		}
	}
	Destroy(&st);
}

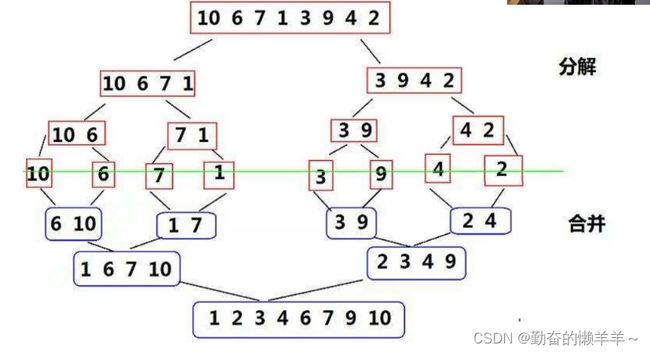
七、归并排序

1、递归版

时间复杂度：N*log（N）

void _MergeSort(int* a, int begin, int end, int* tmp)
{
	if (end <= begin)
		return;
	int mid = (begin + end) / 2;
	//[begin,mid][mid+1,end]递归
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid + 1, end, tmp);
	//[begin,mid][mid+1,end]归并
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
	//把剩下的全放过去
	//注意：这里是闭区间！！！
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2<=end2)
	{
		tmp[i++] = a[begin2++];
	}
	memcpy(a+begin, tmp+begin, sizeof(int)*(end-begin+1));
}

void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc failed\n");
		return;
	}
	_MergeSort(a,0,n-1,tmp);
	free(tmp);
}

2、非递归版（改循环）

void MergeSortNonR(int* a,int n) 
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc failed\n");
		return;
	}
	int gap = 1;//gap是每组数据个数
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)  
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			if (end1>=n || begin2 >= n)
			{
				break;
			}
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			int j = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			memcpy(a+i, tmp+i, sizeof(int)*(end2-i+1)); 
		}
		gap *= 2;
	}
	free(tmp);
}

八、计数排序

如{100,105,105,101,102,100,109,100}

用计数排序的思想做的话就是：

1、找出最大最小的数，（100和109）

2、记录{100，101，102，103，104,105,106,107,108,109}中每个数出现的次数，并用countA数组存起来（此例countA={2,1,1,0,0,2,0,0,0,1}）

3、根据countA就可以排出顺序。

void Sort(int* a, int n)
{
	//找最大最小
	int min = a[0], max = a[0];
	int i;
	for (i = 0; i < n; i++)
	{
		if (a[i] > max)max = a[i]; 
		if (a[i] < min)min = a[i];
	}
	//计数
	int range = max - min + 1;
	int* countA = (int*)calloc(range, sizeof(int));//开一个用来计数的数组
	if (countA == NULL)
	{
		perror("calloc failed");
		return;
	}
	for (int i = 0; i < n; i++)//遍历原数组
	{
		countA[a[i] - min]++;//a[i]-min就是a[i]对应在count的位置
	}
	//放回去
	int j = 0;
	for (int i = 0; i < range; i++)//遍历countA数组
	{
		while (countA[i]--)//同样的数出现的次数
		{
			a[j++] = i + min;
		}
	}
    free(countA);
}

显然，计数排序不适合进行数据分散的排序；相反，若数据比较集中，计数排序的效率是很高的。

九、补充（稳定性）

简单来说，就是看相同的数据在排序前后的相对位置有没有改变，

相对位置不变，则稳定；

相对位置改变，则不稳定；

如冒泡排序，若待排序列为132445，由于两个4相等，所以前后位置并没有改变，因此冒泡排序是稳定的。