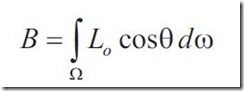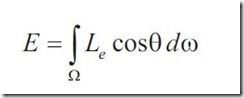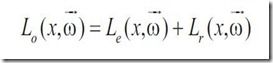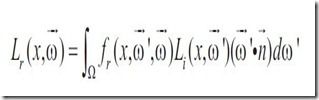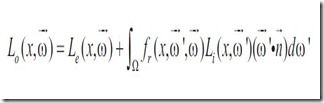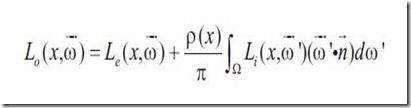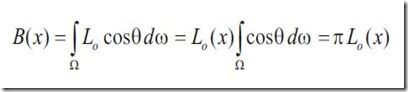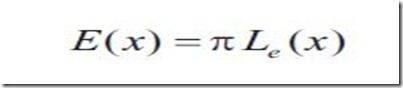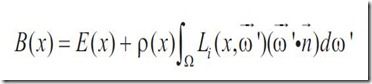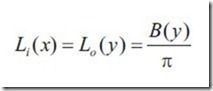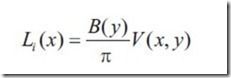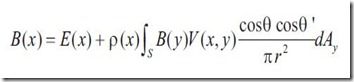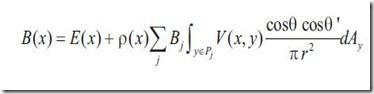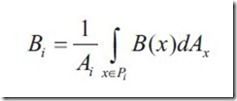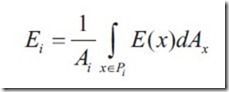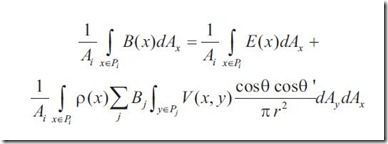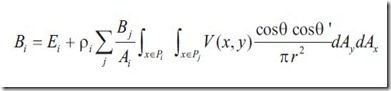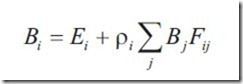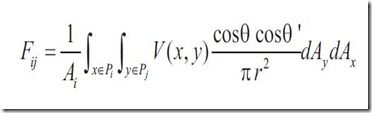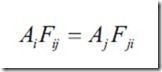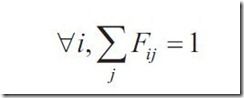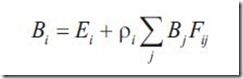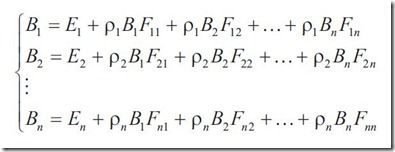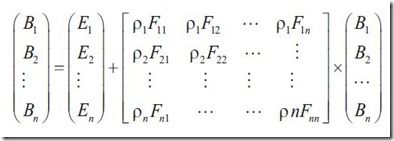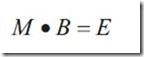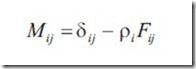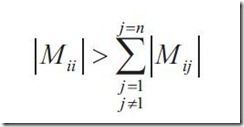Radiosity
Radiosity试图使用不同于光线追踪的方法去考虑全局光照的问题，它将几何图元和场景光照划分为小的元素(called patches)，然后不考虑摄像机的位置，来计算每一个patch的近似渲染方程。因此，Radiosity是一个和视点无关的方法。
1、定义
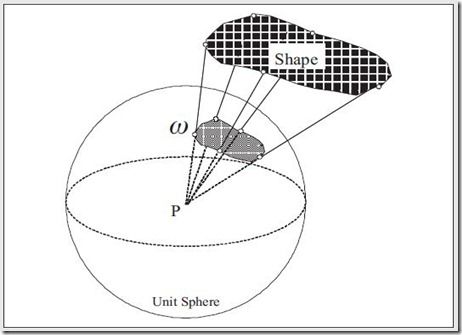
Solid Angle-将物体投影到单位球上所形成的角。如下图角w
solid angle单位是球面度(steradian,sr)，整个单位球的solid angle是4*PI sr。
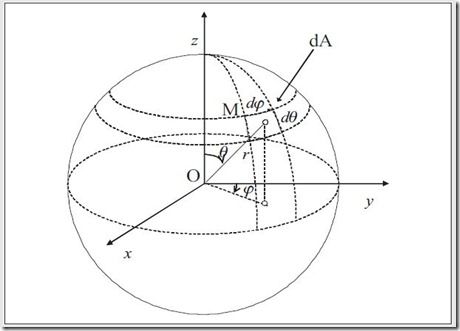
differential solid angle-单位球面上一点的球坐标是(r,theta,phi)，微分表面dA的面积为dA=r^2*sin(theta)d(theta)d(phi)
differential solid angle dw=dA/r^2=sin(theta)d(theta)d(phi)
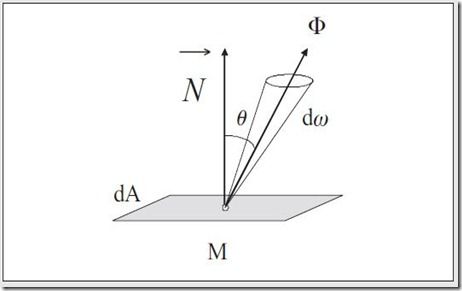
Radiance-Radiosity的量化就是radiance。它是在给定方向上单位solid angle单位面积发射的流量，即W/(sr*m^2)。考虑一块区域dA，其上一点M，从该点出发一条光线，和表面法线的夹角是theta，dw为光线方向上的differential solid angle，O为辐射能量，则radiance L= (dO)^2/(dAdwcos(theta))
radiance不随距离增加而衰减，在传播过程中保持不变
Radiant Exitance-另一个Radiosity的量化，它是离开表面单位面积的能量。表面给定点的radiosity B=dO/dA。
Exitance-表面自发光在单位面积上的能量。
下面来回顾一下已经接触过的渲染方程。最常见的渲染方程如下：
它的含义是：表面特定点x在特定方向w发出的radiance是自发光部分和发射光线部分radiance之和。自发光部分只有当表面可以看做是光源时才考虑，反射光线部分可以看做是在入射光线半球体上对点x的BRDF和入射光线radiance的积分。
所以，渲染方程可以表示为
Radiosity方法是对这个一般方程的数值估算。
2、Radiosity方程
为了简化上面的一般方程，我们会提出一些假设和简化条件。
最重要的假设是只考虑理想的漫反射表面(Lambertian reflector or emitter)。Lambertian表面radiance是常数，和视点向量无关，也就是说，表面发出或者反射光线的分布和入射方向无关。另外BRDF项也是常数，可以从积分里提出来。BRDF项是反射率和PI的比率。
所以简化后的渲染方程是
同时这个假设会有下面有趣的性质
将刚才简化的方程两边同时乘以PI，得到
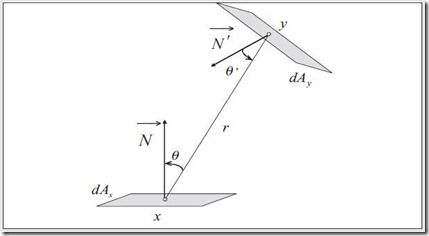
因为radiance有保持不变的性质，所以对于两个点x和y，设可见项为V(x,y)则
加上differential solid angle之后，方程变成
Radiosity的方法是将环境分割成一个一个patch(三角面片或者四边形)，上面公式对所有表面的积分可以转化成作用在不同patch上的和，假设每一个patch上有恒定的radiosity，这导致公式的进一步变形
对于一个patch，恒定的radiosity是
恒定的自发光是
之前的渲染方程作用在给定表面的给顶点上，如果以patch为单位，需要对patch上的点进行积分，如下
因为给定patch中反射率恒定，所以有
这就是Radiosity方程，他表达了给定patch的radiosity和patch自发光分量加其他所有patch对其radiosity的关系。form factor F可以有下式给出
radiosity方法就是怎样高效计算form factor，然后求解出方程。
3、Form Factor
如果两个patch不能相互可见，则F=0，否则F>0
Form Factor有交换性
在一个封闭环境中有
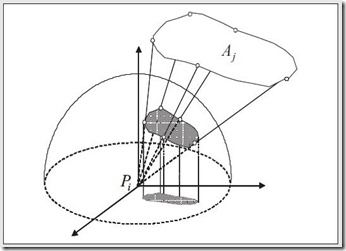
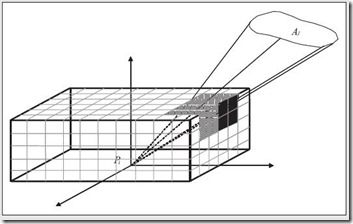
为了求解form factor，我们使用数值分析的方法，具体来说就是使用投影方法。Nusselt方法(将patch投影到单位球上)和hemicube方法(将patch投影到单位半立方体上)。两种方法中，我们假设两个patch的F计算可以简化成一个点和一个patch的F计算，当两个patch的距离远远大于patch大小的时候该假设成立。
Nusselt方法中，单位半球体位于接受光照的patch中心，发射光照的patch首先投影到半球上，然后投影到平面上。
Hemicube方法普遍使用于计算F的过程中，使用单位半立方体取代上面的半球，该半立方体均匀划分为网格，接着patch投影到半立方体的五个面中，对于每一个网格，将会计算一个deltaF，总的F是所有deltaF的和。
该方法一个重要的参数是网格的细分度。
4、Radiosity的经典计算方法
Radiosity方程如下
该方程可以转化为一系列的线性方程组
化成矩阵形式为
整理该方程可得
E已知，所以要解出B，只需要求矩阵M的逆。
当i=j时，Kronecker项为1，否则为0
对于每一个patch，反射率已知，所以要得到最后的解，需要求出form factor，然后对矩阵M求逆。
流程：
a、将环境(光照和几何体)划分为patch
b、计算每一对patch的form factor
c、通过求解线性方程组计算radiosity方程
d、通过计算好的radiosity，绘制出结果(因为radiance和radiosity成正比)。
两种数值迭代方法可以用来求解线性方程组-Jacobi和Gauss-Seidel。
两种方法都使用了矩阵M的一个性质，即diagonal dominance
