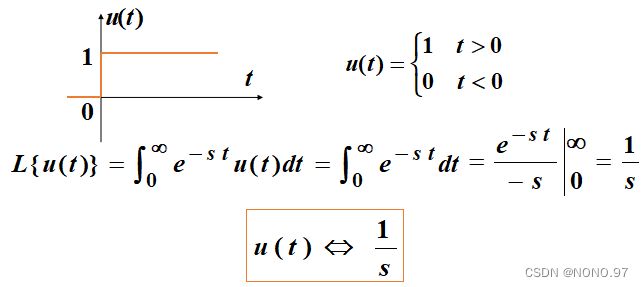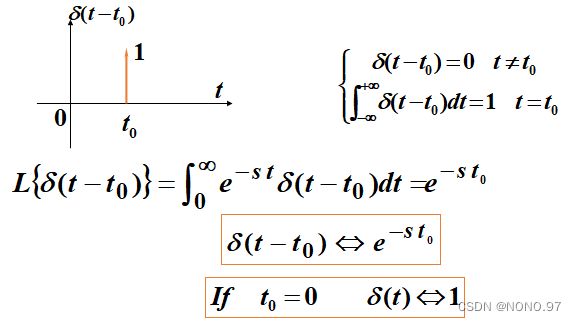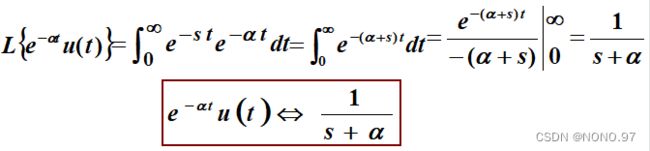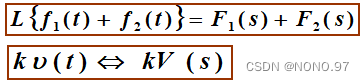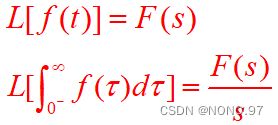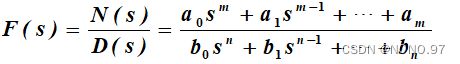【知识点总结】电路原理 第二讲

电路原理 第二讲

总结内容：
内容包括：二端口网络参数及连接方式、拉普拉斯变换常见函数及部分分式展开法、复频域内的电路定律与元件模型、复频域内的运算法、关联矩阵、回路矩阵、割集矩阵、特勒根公式、各矩阵之间的关系、结点法分析矩阵方程、回路法分析矩阵方程、状态方程、小信号分析法。

---

提示：本文章是本人结合所学的课程进行总结所写，如果大家感兴趣，直接从目录里找需要的看。本文很长，切忌一口气读完

---

前言

简介：

本文承接上一讲所讲，完成我所学的内容总结。
本人学艺不精，有一些知识点地方可能存在瑕疵，希望各位大佬可以多多指教。

---

提示：以下是本篇文章正文内容

第九章——二端口网络

**传统一端口网络：**只通过一对端钮与外电路相连，则称为“一端口网络”。
二端口网络：

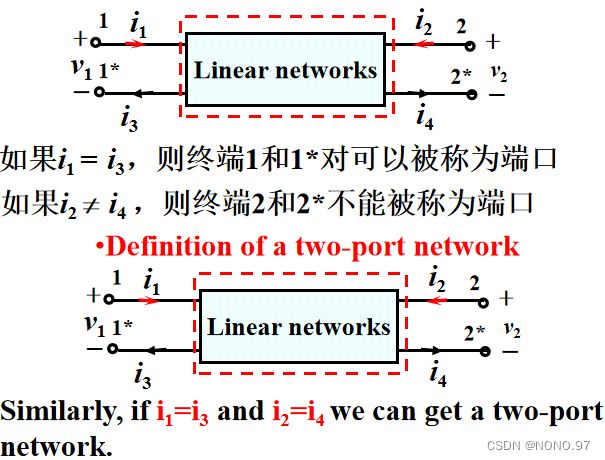
一.二端口网络的参数

二端口网络的参数可分解为 Y、Z、H 和 T 。
其意义：首先，这种网络在通信、控制系统、电力系统和电子方面很有用。其次，知道了双端口网络的参数，我们就可以把它当作嵌入到更大的网络中的“黑匣子”。

1.Y参数

Y参数：当一端短路时的导纳参数。

当 Y12 = Y21 时，该网络为互易二端口网络，激励无论加在哪侧，对侧产生的响应都一样，其四个参数中只有三个是独立的。
当 Y11 = Y22 时，该网络为对称二端口网络，两个端口外特性(己侧/对侧)完全一样，对称二端口只有两个参数是独立的。
获取该参数的方法：
方法一：（1）输出端短路（即V2 = 0），可求解出 Y11 和 Y21。
（2）输入端短路（即V1 = 0），可求解出 Y22 和 Y12。
方法二：利用 KCL 进行求解方程。

2.Z参数

**Z参数：**当一端开路时的阻抗参数。

获取该参数的方法：
方法一：（1）输出端开路（即I2 = 0），可求解出 Z11 和 Z21。
（2）输入端开路（即I1 = 0），可求解出 Z22 和 Z12。
方法二：利用 KVL 进行求解方程。

3.H参数（混合参数）

H参数混合参数的使用非常适合于晶体管电路，因为这些参数是最方便测量的对于晶体管来说是实验。
Z参数：当一端开路，另一端短路时的参数。

对于互易二端口网络： H12 = - H21；对于对称二端口网络：H11 H22 - H12 H21 = 1
获取该参数的方法：
方法一：（1）输出端短路（即V2 = 0），可求解出 H11 和 H21。
（2）输入端开路（即I1 = 0），可求解出 H22 和 H12。
方法二：利用 KVL、KCL 进行求解方程。

4.T参数（传输参数）

T参数：当同一端先开路，再短路时的参数。

对于互易二端口网络： AC - BD = 1；对于对称二端口网络：A = D
获取该参数的方法：
方法一：（1）输出端短路（即V2 = 0），可求解出 B 和 D。
（2）输出端开路（即I2 = 0），可求解出 A 和 C。
方法二：利用 KVL、KCL 进行求解方程。
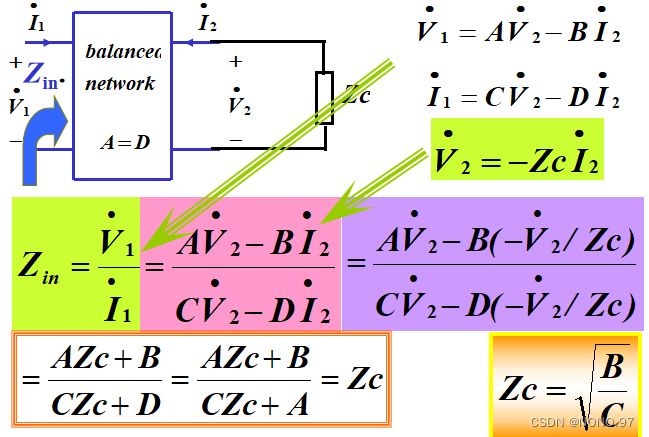
引申——特性阻抗 Zc：对于平衡(对称)二端口网络，我们可以选择一个负载阻抗Zc，即输入阻抗Zin。经过化简后可得Zc = √（B / C）

小结

双端口网络的Z和H参数并不总是存在。

二.二端口网络的连接方式

为了分析和设计的目的，可以将一个大型复杂网络划分为若干子网。这些子网被建模为双端口网络，相互连接形成原始网络。因此，双端口网络可以被视为可以相互连接以形成复杂网络的构建模块。互连可以是串联、并联或级联的。
串联：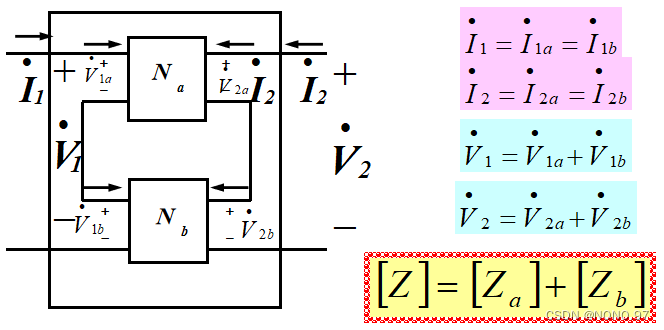
并联：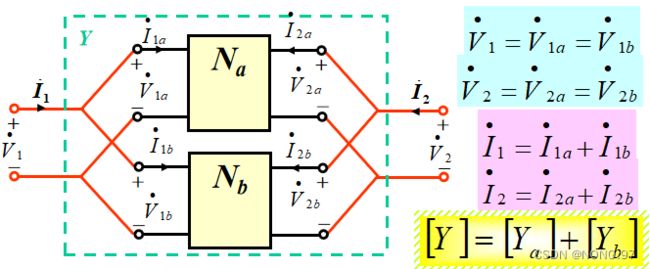
级联：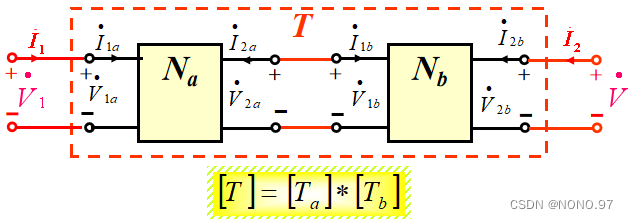

三.回转器和负阻抗变换器

1.回转器

**回转器:**具有将一个端口的电流“旋转”到另一个端口的电压的特性（感觉有点像受控源的意思）。由于电感本身体积庞大且难以调节，因此旋转器的上述特性可用于模拟晶体管和集成电路中所需的电感。**回转器的一个重要应用：**模拟电感器。

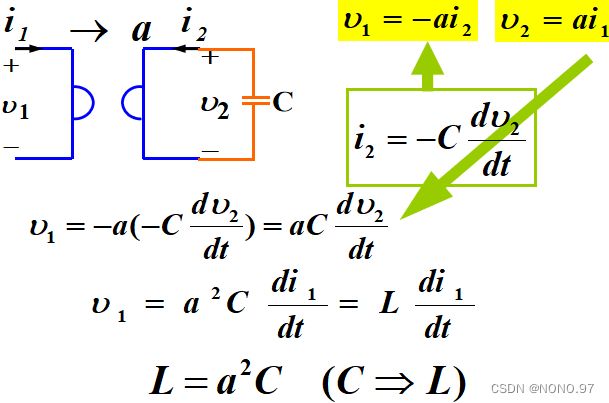
2.负阻抗变换器NIC

**NIC：**具有将普通阻抗变为负阻抗的性质。（主要利用i1 、i2 电流方向不一致）

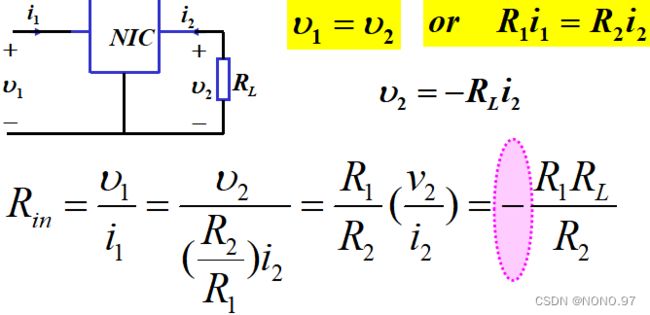
第十章——拉普拉斯变换法

这里的与复变函数类似，不具体讲述，仅展开结论。

一.拉普拉斯变换法的定义

（1）在电路中我们用U(s)和I(s)分别表示u(t)和i(t)的拉普拉斯变换。
（2）u(t)和i(t)是时间的函数，即时域变量 ,是实际存在的变量，而U(s)和I(s)则是一种抽象的变量。之所以把直观的时域变量变为抽象的复频率变量，是为了便于分析和计算电路问题，待得出结果后再反变换为相应的时域变量。

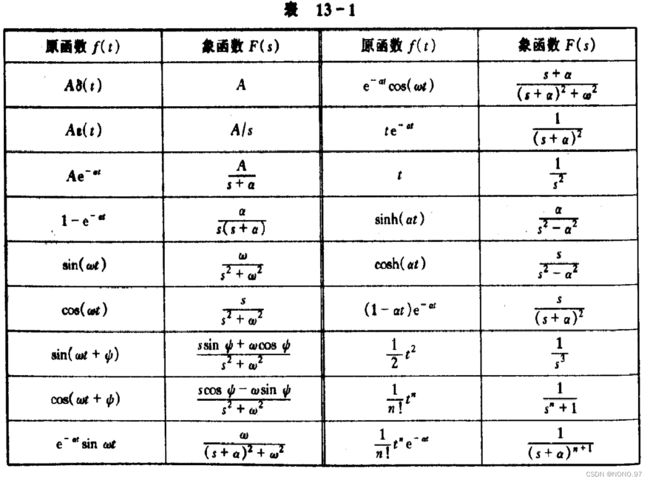
二.几个常见的拉普拉斯变换

1.单位阶跃函数

2.冲击函数

3.指数函数

4.斜坡函数

三.拉普拉斯变换的性质

1.线性性质

2.微分性质

3.积分性质

4.延迟性质

5.卷积

四.部分分式展开法

**从f(s)中求f(t)的方法:**可以通过列定义方程求解、查拉氏变换表、或是将复杂的F(s)分解成简单的F(s)的组合，然后找到表格。本段将重点讲述部分分式展开法来列写拉普拉斯变换。
对于任意形式的F(s)可化简为以下形式：

1.n > m时

（1）常规解法：通过化简求出其 D(s) 的各个单根，通过洛必达法则将分母求导，代入各个单根取得其系数，即可得到简易的F(s)，其可通过拉普拉斯变换求得f(t)。

（2）当根为共轭复根时，解法类似。

（3）当根为重根时，解法类似，不同的是对于重根所在的分子进行不同次幂的求导。

2.n <= m时

可将分数进行拆分，直至拆分式子的分数为 n’ > m’ 的形式，进而求解。

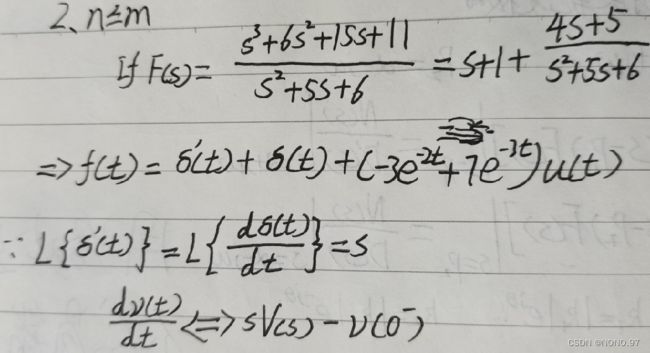
小结：

五.复频域中的电路定律与电路模型

1.电路定律

复频域中的 KCL、KVL 等仍适用。

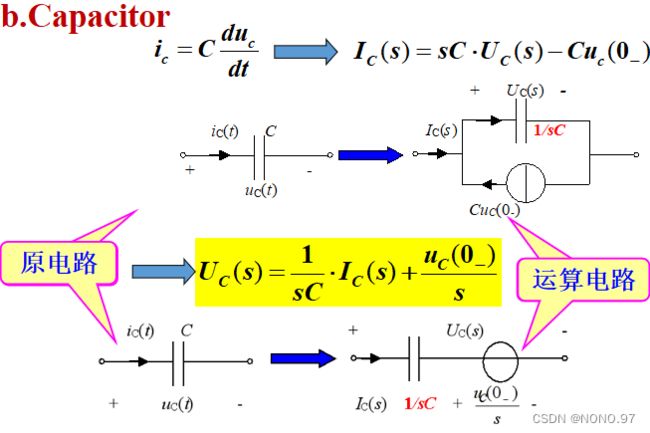
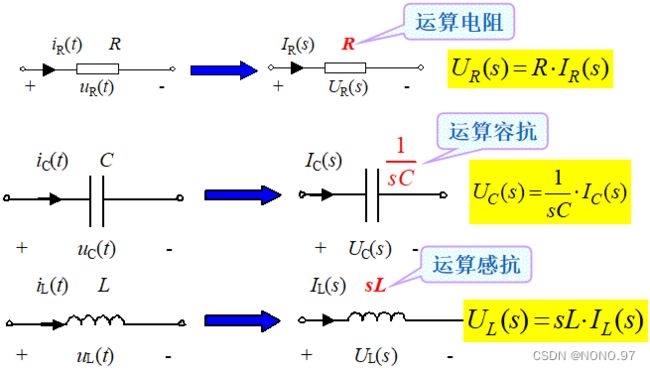
2.电路中各元件

（1）电阻

（2）电容
（3）电感

3.当动态元件初始储能为零时：

电阻不变、电感电容发生改变。

六.运算法

运算法与相量法的基本思想类似，相量法把正弦量变换为相量(复数)，从而把求解线性电路的正弦稳态问题归结为以相量为变量的线性代数方程。运算法把时间函数变换为对应的象函数，从而把动态电路问题归结为求解以象函数为变量的线性代数方程。
当电路的所有独立初始条件为零时，电路元件的运算形式与相量形式是类似的，加之 KCL 和 KVL 的运算形式与相量形式也是类似的，所以对于同一电路列出的零状态下的运算形式的方程和相量方程在形式上相似，但这两种方程具有不同的意义。在非零状态条件下，电路方程的运算形式中还应考虑附加电源的作用。但当电路中的非零独立初始条件考虑成附加电源之后，电路方程的运算形式仍与相量方程类似。
可见相量法中各种分析方法和定理在形式上完全可以移用于运算法。

1.运算步骤：

（1）由换路前电路计算uc(0-) , iL(0-) 。
（2）画运算电路模型。
（3）应用电路分析方法求象函数。
（4）反变换求原函数。

2.传递函数 H(s)

我们定义传递函数H(s)为当所有初始条件为零时，系统输出(或响应)的拉普拉斯变换Vo(s)与输入(或强迫函数)Vi(s)的拉普拉斯变换之比。

极点位置不同，响应性质不同。一个实际的线性电路，其网络函数的极点一定位于左半平面。

第十一章——网络拓扑学

图论是数学中重要的分支，电网络图论是图论在电路理论中的应用。主要通过电路的结构及其连接性质，对电路进行分析计算。

一.基本概念

1.基本概念

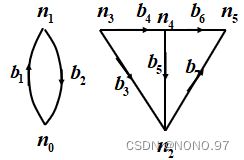
（1）节点：节点 ni 被定义为线段的端点或一个孤立的(孤立)点。
（2）支路：分支 bk 是一条线段，它的端点有两个节点 ni 和 nj 。
（3）图：图G是节点和分支的集合，其条件是分支仅在节点处相交。
（4）度：节点的度是关联到它的分支的数量。
（5）路径：长度为m的路径是一个序列(序列)，由m个不同的分支和m+1个不同的节点组成，除初始节点和终端节点为1次外，每个节点都为2次。
（6）回路：长度为m的环路是这样的路径，其初始节点和终端节点重合。
（7）连通图：如果图G中的任意两个节点之间至少有一条路径，则图G是连通的。
（8）**树：**连通图G的树T是G的连通子图，具有以下性质：T包含G的所有节点、T不包含任何回路。其中树支数bT=n-1。不是树形分支的G的分支称为连枝或和弦。
（9）基本回路：只含一条连支的回路称为单连支回路，它们的总和为一组独立回路。
**需注意：**树一经选定，基本回路唯一地确定下来。对于平面电路而言，其全部网孔是一组独立回路。
（10）**割集：**一个连通图的割集是一个最小分枝数量的集合，当删除时将图划分为两个独立的子图或部分，如果这些被删除的分支中有一个没有被删除，那么图仍然是连通的。
**连通图G中支路的集合，具有下述性质：**把Q中全部支路移去（保留节点） ，图分成二个分离部分。任意放回Q 中一条支路，仍构成连通图。
（11）基本割集：只含有一个树枝的割集。割集数＝n-1

2.注意：

（1）连支集合不能构成割集。
（2）属于同一割集的所有支路的电流应满足 KCL 。当一个割集的所有支路都连接在同一个结点上，则割集的 KCL 方程变为结点上的 KCL 方程 。
（3）对应一组线性独立的KCL方程的割集称为独立割集 ，基本割集是独立割集，但独立割集不一定是单树支割集。

3.图的矩阵表示

图的矩阵表示是指用矩阵描述图的拓扑性质，即KCL和KVL的矩阵形式。有三种矩阵形式：

二.关联矩阵和基尔霍夫定律

1.关联矩阵

用矩阵形式描述结点和支路的关联性质。n个结点b条支路的图用 n x b 的矩阵 Aa 描述 ：

2.关联矩阵与KCL、KVL

矩阵形式的 KCL: A ib = 0
矩阵形式的 KVL: 【u】 = 【A】^T【un】

三.回路矩阵和基尔霍夫定律

1.回路矩阵

独立回路与支路的关联性质可以用回路矩阵Ba描述。

2.基本回路矩阵Bf

独立回路对应一个树的单连枝回路得基本回路矩阵 [Bf]，其连支电流方向为回路电流方向、支路排列顺序为先连支后树支，回路顺序与连支顺序一致。

3.回路矩阵与KCL、KVL

矩阵形式的KCL： Bf^Til =i
矩阵形式的 KVL ：Bf u = 0

四.割集矩阵和基尔霍夫定律

1.割集矩阵

割集与支路的关联性质可以用割集矩阵Qa描述。

2.基本割集矩阵Bf

**划分依据：**割集方向为树支方向；支路排列顺序先树支后连支；割集顺序与树支次序一致。

3.割集矩阵与KCL、KVL

矩阵形式的KCL：[Qf ] [ i ] = 0
矩阵形式的 KVL ：[Qf ]^T [ut ] = [u]

五.各类型矩阵之间的相互关系

存在以下关系，不进行推导。

六.特勒根公式

特勒根公式所得出的结论不能被解释为能量守恒，它仅仅是一种数学关系，存在于同一拓扑结构的一个电路的支路电压和另一个电路的支路电流之间

公理1（功率守恒）

一个给定的集总网络的所有支路传递或吸收的功率之和为零。

公理2

vb、ib为一个状态的值，vb’、ib’为另一个状态的值，则有vb^T ib’ = 0、 vb’^T ib = 0。

第十二章——网络的矩阵方程

一.矩阵方程的回路法

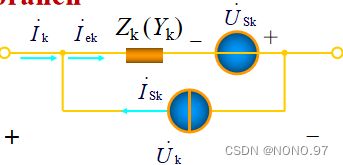
1.支路的特性

（1）独立电压、独立电流和支路电压、支路电流的方向相反（Usk 与 Isk 的方向与 ib 、 vb 相反）。
（2）方向与支路电压和支路电流有关（ib 与 vb 是关联的）。
（3）支路阻抗(或导纳) Zk (Yk) 可以是单个电阻、电容或电感，而不是它们的组合。

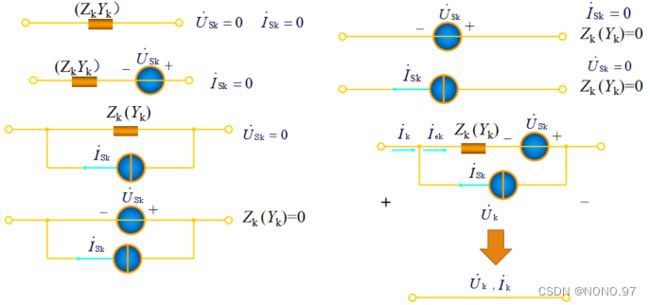
2.一些典型案例

3.支路阻抗矩阵

（1）电路中电感之间无耦合

（2）电路中电感之间有耦合


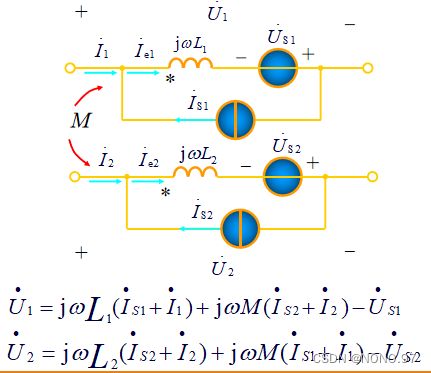
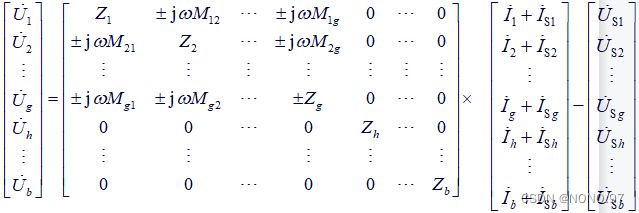
（3）电路中有受控电压源

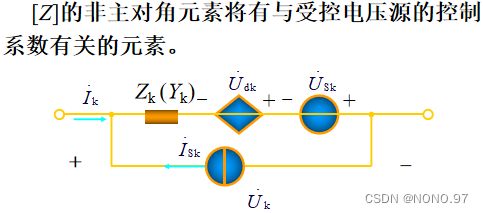
4.支路阻抗矩阵回路电流方程的矩阵形式

5.总结——步骤

（1）求出电路中的 [B]、[Z]、[Us]、[Is]。
（2）找到 [Zl]、[Ul]，并写出回路矩阵—— [Zl] [il] = [Uls]。
（3）求出 [il] 后由 KCL 解出 [Ub]、[Ib] —— [Ib] = [B]^T [il]

二.矩阵方程的节点法

该方法与回路法类似。

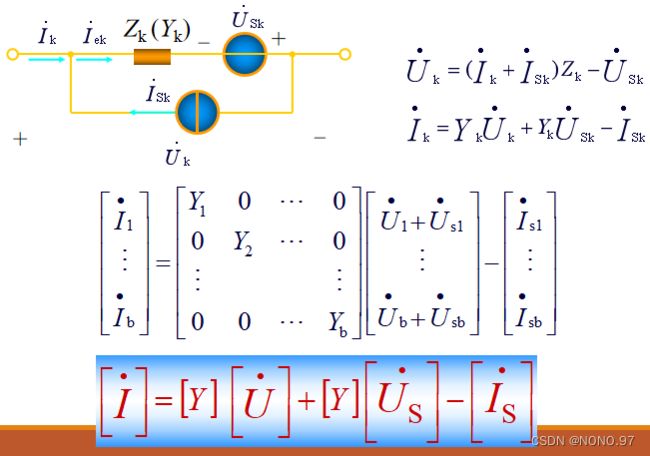
1.支路导纳矩阵形式

（1）电路中不含互感和受控源

（2）电路中电感之间有耦合

（3）电路中有受控源

2.结点电压方程的矩阵形式

3.总结——步骤

（1）把电路抽象
（2）写出关联矩阵 [A]
（3）写出导纳矩阵 [Y]、[Us]、[Is]。
（4）找到用矩阵乘法求得结点方程。

三.状态方程分析动态电路

1.状态变量

其为分析动态过程的独立变量。选定系统中一组最少数量的变量 X = [x1,x2,…xn]^T ，如果当 t = t0 时这组变量X(t0)和 t >= t0 后的输入 e(t) 为已知，就可以确定 t0 及 t0 以后任何时刻系统的响应 Y(t) 。称这一组最少数目的变量为状态变量。

2.状态方程

其为求解状态变量的微分方程。

**状态方程的特点：**一阶微分方程组、左端为状态变量的一阶导数、右端仅含状态变量和输入量。

3.输出方程

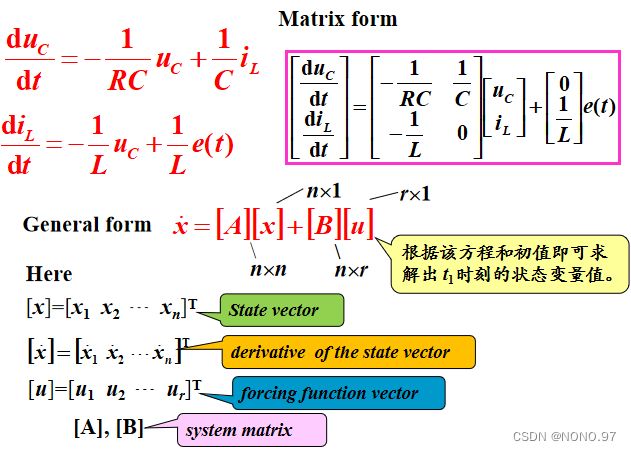
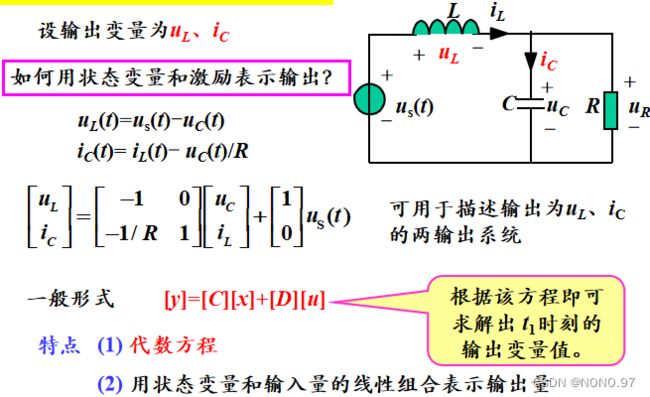
其为用状态变量表示输出的代数方程。

4.列写状态方程的方法

用电容电压和电感电流的线性组合来表示电容电流和电感电压。

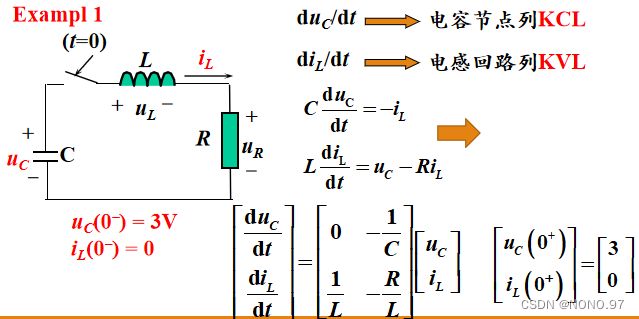
步骤：
（1）找出一个“树”。
（2）假定电压电流的变量。
给每个电容分配一个电压(带极性参考)，给每个电感分配一个电流(并带箭头);这些是状态函数。如果可能的话，根据源电压、源电流和状态变量，指出每个树枝上的电压和每根弦上的电流;否则，分配一个新的电压或电流变量到该电阻树分支或弦。
（3）列写电容C的方程（KCL）
（4）列写电感L的方程（KVL）
（5）列写电阻R的方程
（6）列写状态方程

第十三章——小信号分析法求解非线性电路

1.非线性的基本应用

**非线性特点：**无齐次性，无可加性，常应用于整流、稳压、放大、震荡、变频、开关电路。

2.小信号分析法

将变化的电源分为一个稳定的稳定的电源和一个时变的电源，通过找其静态工作点、动态电阻或电导，画出等效小信号电路，并计算出小信号电路的响应，通过小信号响应与静态工作点相叠加即可得到非线性电路的响应。
步骤：
（1）求解非线性电路的静态工作点。
（2）求解非线性电阻在该静态工作点处的动态电阻或电导。
（3）画小信号等效电路，求解其响应。
（4）将小信号响应与静态工作点相叠加合并。

总结

小小的总结：

以上就是我在电路原理中所学的内容，本文仅仅简单总结了电路原理的相关知识，大家如果想要深入了解电路原理的相关知识，不妨参考一下相关的专业书。
终于完成了，(✪ω✪)，继上一讲结束之后，花了近3天的时间才完成对第二讲的总结，由于时间有些仓促，可能有些地方存在着一些问题，希望大家多多包涵。接下来我将更新模电、数电、电力电子器件等相关知识总结。
注：里边的内容、见解有些小问题，希望各位大佬可以多多指教。

学习资料附件：

链接：https://pan.baidu.com/s/1rf_DbLVWvOvX1voSUkwsCw
提取码：j50e