第五十八章 线段树（一）

一、树状数组的缺陷

在前面两个章节中，我们利用树状数组去维护的是前缀和数组和差分数组。当我们去查询 区间和的时候，我们采用的方法是两个前缀和相减。也就是说，如果我们想求某个区间的性质就必须将其转化为两个前缀的性质相减。只有满足这个条件的时候，我们才能使用树状数组。但是有的性质并不满足这个条件，比如说我们想求一个区间最大值的时候，我们并不能将其转化为两个前缀的最大值相减。

所以说，当我们求某些特殊的区间性质的时候，树状数组就很难做到了。但是如果是求前缀的性质，树状数组还是很好用的。

那么为了解决高效求区间性质的问题，就需要用到今天所讲解的线段树。

二、线段树的作用

线段树能做到的恰恰就是树状数组不能做到的。线段树最重要的作用就是通过$O(log(n))$的时间复杂度去维护或查询某个区间的性质。

三、线段树的基本构成

1、节点定义

struct Node
{
	int l, r;//区间的左右端点
	int v;//该区间的性质
}；

2、线段树的结构

线段树是一个二叉树。假设一个节点代表的区间是$[l,r]$，然后我们将这个区间一分为2，左边的区间就是该节点的左子树，右边的区间就是该节点的右子树。
如下图所示：

（选自百度百科）

四、线段树的重要函数

1、构造线段树——bulid函数

void build(int u, int l, int r)
{
	tre[u] = {l, r};
	if(l == r)
		return;
	int mid = l + r >> 1;
	build(u << 1, l, mid);
	build(u << 1 | 1, mid + 1, r);
}

$u$指的是节点标号，$l$和$r$是该节点所代表的区间的左右端点。当我们的根节点标号是$1$的时候，我们的左右子节点分别是$(2\ast u)$和$(2\ast u+1)$，如果写成位运算的模式即：$(u<<1)$和$(u<<1|1)$。最小的区间即区间左端点等于区间右端点的时候，此时该区间所在的树中节点也恰好是我们的叶子节点。

2、查询区间——query函数

如上图所示，假设我们的线段树维护的是区间的最大值，我们现在的目的是求红色区域所构成的区间的最大值。

想要求红色区间最大值的话，我们只需要找到图中三段的绿色区间的最大值，然后三个区间比较一下即可。

现在我们的难点是如何找到这三个绿色区间。

不难发现，这三个区间都是被红色区间包含的，所以只要某个节点所代表的区间被包含在我们所求区间里，我们就返回这个区间的最值，然后再所有返回的最值中比较一个最大值作为答案。

int query(int u, int l, int r)
{
	if(tre[u].l >= l && tre[u].r <= r)
		return tre[u].v;
	int mid = tre[u].l + tre[u].r >> 1;
	int res = 0;
	if(l <= mid)
		res = query(u << 1, l, r);
	if(r > mid)
		res = max(res, query(u << 1 | 1, l, r));
	return res;
}

3、单点修改——modify函数

单点修改的操作比较麻烦，我们可以将单点修改的操作画成下面的图。

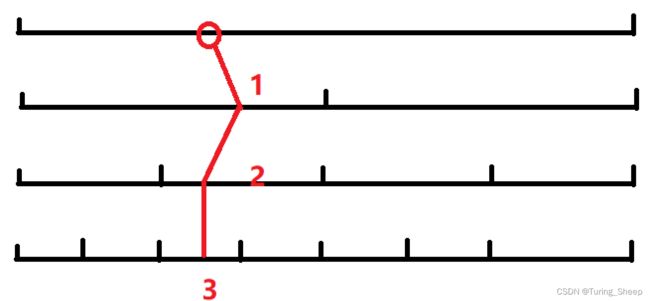
假设上面这个图的最后一层就是叶子节点。叶子节点所代表的区间就是一个点，所以我们单点修改一定对应着某个叶子节点，我们现在的目的就是去找到这个点。然后对这个点进行修改。

这里还有一个问题，这个单点被包含在若干区间内，当我们修改了这个单点后，所有包含这个点的区间也需要被更新。也就是说我们在回溯的时候，还要利用子节点去更新一下父节点。这个利用子节点更新父节点操作写成：$pushup$。

void pushup(int u)
{
	tre[u].v = max(tre[u << 1].v, tre[u << 1 | 1].v);
}

void modify(int u, int x, int v)
{
	if(tre[u].l == x && tre[u].r == x)
		tre[u].v = v;
	else
	{
		int mid = tre[u].l + tre[u].r >> 1;
		if(x <= mid)
			modify(u << 1, x, v);
		else
			modify(u << 1 | 1, x, v);
		
		pushup(u);
	}
}

五、例题

AcWing1275. 最大数

参考代码：

#include
#define endl '\n'
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 2e5 + 10;
struct Node
{
	int l, r;
	int v;
}tre[4 * N];
int m, p;


void build(int u, int l, int r)
{
	tre[u] = {l, r};
	if(l == r)
		return;
	int mid = l + r >> 1;
	build(u << 1, l, mid);
	build(u << 1 | 1, mid + 1, r);
}

int query(int u, int l, int r)
{
	if(tre[u].l >= l && tre[u].r <= r)
		return tre[u].v;
	int mid = tre[u].l + tre[u].r >> 1;
	int res = 0;
	if(l <= mid)
		res = query(u << 1, l, r);
	if(r > mid)
		res = max(res, query(u << 1 | 1, l, r));
	return res;
}

void pushup(int u)
{
	tre[u].v = max(tre[u << 1].v, tre[u << 1 | 1].v);
}

void modify(int u, int x, int v)
{
	if(tre[u].l == x && tre[u].r == x)
		tre[u].v = v;
	else
	{
		int mid = tre[u].l + tre[u].r >> 1;
		if(x <= mid)
			modify(u << 1, x, v);
		else
			modify(u << 1 | 1, x, v);
		
		pushup(u);
	}
}


void solve()
{
	 int n = 0, last = 0;
    scanf("%lld%lld", &m, &p);
    build(1, 1, m);

    int x;
    char op[2];
    while (m -- )
    {
        scanf("%s%lld", op, &x);
        if (*op == 'Q')
        {
            last = query(1, n - x + 1, n);
            printf("%lld\n", last);
        }
        else
        {
            modify(1, n + 1, ((ll)last + x) % p);
            n ++ ;
        }
    }

}

signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	solve();
}