（三）SVM项目-乳腺癌预测

今天继续练习SVM的使用，打算明天过一遍算法推导，这之前还是多做项目，熟悉使用方法。
数据来自UCI repository http://archive.ics.uci.edu/ml/datasets/breast+cancer+wisconsin+%28diagnostic%29

【导入并查看数据】

from sklearn import svm
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn import preprocessing
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix

path='D:/data_analysis/jupyter_notebook/machine_learning/dataset/breast-cancer.csv'
df=pd.read_csv(path)
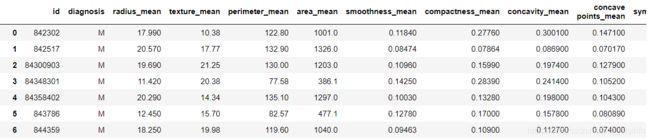
df

569 rows × 33 columns

df.info()

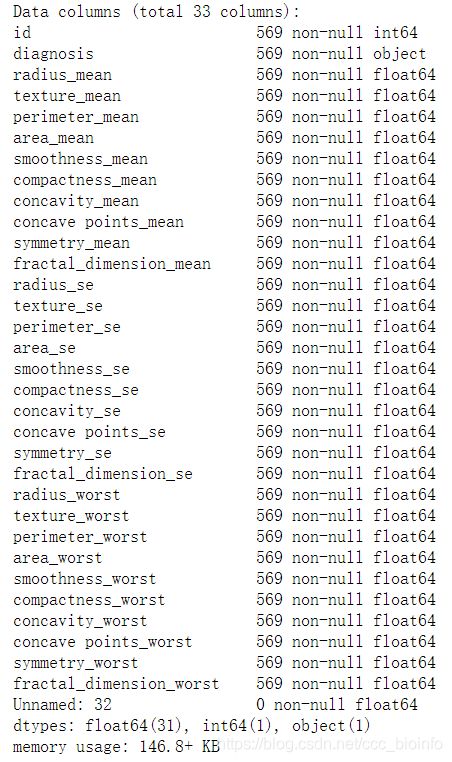
由图可知，一共32列，第一列是id，第二列是诊断信息（B-正常，M-患癌），其余30列是从乳腺肿块的细针抽吸（FNA）的数字化图像计算特征，它们描述了图像中存在的细胞核的特征，分为三类，为每个图像计算这些特征的平均值，标准误以及“最差”，mean，se，worst，谷歌翻译如下：

①半径（从中心到外围点的距离的平均值）
②纹理（灰度值的标准偏差）
③周长
④区
⑤平滑度（半径长度的局部变化）
⑥压实度（周长^ 2 /面积-1.0）
⑦凹度（轮廓凹部的严重程度）
⑧凹点（轮廓的凹入部分的数量）
⑨对称
⑩分形维数（“海岸线近似”-1）

【数据清洗】
由以上info()可以看到无缺失值，所以只需删除id列和转换diagnosis列。

#数据清洗
#删除id列
df.drop('id',axis=1,inplace=True)
#转换diagnosis列，B为正常，M为患病
df['diagnosis']=df['diagnosis'].map({'B':0,'M':1})

【特征选择】

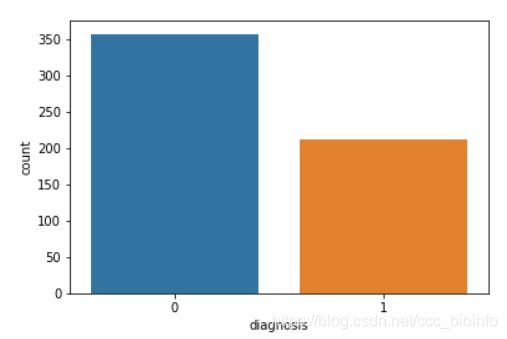
#将肿瘤的结果可视化
sns.countplot(df['diagnosis'],label='Count')

#用热力图展现feature-mean字段之间的相关性
corr=df[features_mean].corr()
plt.figure(figsize=(14,14))
#annot=True 显示每个方格的数据
sns.heatmap(corr,annot=True)

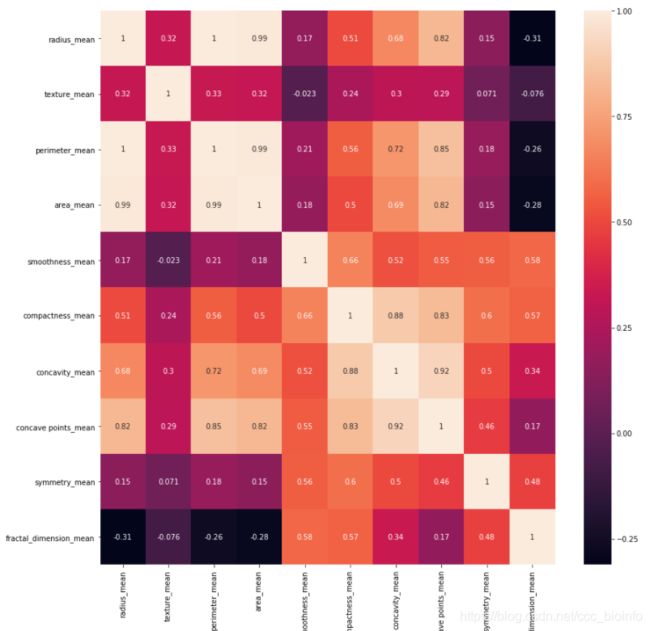
颜色越浅为相关性大的特征，如果相关性大则从中选取其中一个特征作为代表即可。
从上面的图中可以看出来:
radius_mean,parameter_mean,area_mean 相关性特别大，
compactness_mean,cavity_mean,concave points_mean相关性特别大，
所以选取其中一个作为代表即可，至于选择哪个特作为代表，结果不会有特别大的影响。

特征选择的目的是降唯，用少量的特征代表数据的特性，这样也可以增强模型的泛化能力，避免数据过拟合。

在本次特征选择中，我们选择忽略掉se，和worst 特征。
因为这些特征都是对于同一个数据的不同表达方式，
这样的话，我们就可以从30个特征当中选择10个特征，又根据上面的相关性数据，还剩下6个特征。

#因此特征选择如下：
features_remain=['radius_mean','texture_mean','smoothness_mean',
                   'compactness_mean','symmetry_mean','fractal_dimension_mean']

#抽取30%的数据作为测试集，其余为训练集
train,test=train_test_split(df,test_size=0.3)
train_x=train[features_remain]
train_y=train['diagnosis']
test_x=test[features_remain]
test_y=test['diagnosis']

#对数据进行z-score归一化
ss=preprocessing.StandardScaler()
train_x=ss.fit_transform(train_x)
test_x=ss.fit_transform(test_x)

【模型创建】

#模型创建
model=svm.SVC(random_state=0)
model.fit(train_x,train_y)
prediction=model.predict(test_x)
print(accuracy_score(prediction,test_y))

得到的准确率为：0.9473684210526315

再利用混淆矩阵计算

cm=confusion_matrix(test_y,prediction)
cm

array([[103, 5],
[ 4, 59]]

---

---

---

再尝试发现，kernel=’rbf‘（默认值）可以得到最高的准确率，即如上所示的94%，但还是不够高。
所以改变特征选择，这次试了全部的特征。

features_remain=[ 'radius_mean', 'texture_mean', 'perimeter_mean',
       'area_mean', 'smoothness_mean', 'compactness_mean', 'concavity_mean',
       'concave points_mean', 'symmetry_mean', 'fractal_dimension_mean',
       'radius_se', 'texture_se', 'perimeter_se', 'area_se', 'smoothness_se',
       'compactness_se', 'concavity_se', 'concave points_se', 'symmetry_se',
       'fractal_dimension_se', 'radius_worst', 'texture_worst',
       'perimeter_worst', 'area_worst', 'smoothness_worst',
       'compactness_worst', 'concavity_worst', 'concave points_worst',
       'symmetry_worst', 'fractal_dimension_worst']

得到的准确率为0.9766081871345029，有较大提高。
混淆矩阵结果为：
array([[104, 2],
[ 2, 63]]。

至此，此项目完成。
过程中的收获：
（1）特征选择：用curr（）来计算特征间的相关性，距离较近的可以选其一。
（2）计算准确率既可以用混淆矩阵，也可以用sklearn.metrics的accuracy_score。