leetcode hot 100 - 5. 最长回文子串

5. 最长回文子串

题目描述：

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

示例 2：

输入: "cbbd"
输出: "bb"

思路一：中心扩展法

参考：https://leetcode-cn.com/problems/palindromic-substrings/solution/liang-dao-hui-wen-zi-chuan-de-jie-fa-xiang-jie-zho/

选定中心点后，同时判断左右字符是否相等，如果相等，则构成了回文子串，再继续向左右扩张，判断是否能形成更长的回文子串。

首先每个字符都可以是中心点，其次所有相邻的两个字符也可以中心点，比如abba, 如果以单个字符中心点，那么abba这最长的回文子串就永远统计不到，但是如果以 bb 为中心点，则能统计到这个回文子串。

至于为什么三个相邻的字符，四个相邻的字符不是中心点，因为三个相邻的字符可以是单个中心点扩展一次得到，四个相邻的字符可以是两个相邻的字符扩展一次得到。所以中心点的个数为 2n-1, n 字符串长度。

 1 class Solution {
 2     public String longestPalindrome(String s) {
 3         // 中心扩展法
 4         if(s == null){
 5             return null;
 6         }
 7         int maxLength = 0;      // 当前回文子串的最大长度
 8         String maxPalindrome = "";
 9         int len = s.length();
10         for(int center = 0; center < 2 * len - 1; center++){
11             int left = center / 2;
12             int right = center / 2  + center % 2;
13             while(left >= 0 && right < len && s.charAt(left) == s.charAt(right)){
14                 if(right - left + 1 > maxLength){
15                     maxLength = right - left + 1;
16                     maxPalindrome = s.substring(left, right + 1);
17                 }
18                 left--;
19                 right++;
20             }
21         }
22         return maxPalindrome;
23     }
24 }

leetcode 执行用时：40 ms > 51.97%, 内存消耗：39.3 MB > 55.85%

复杂度分析：

时间复杂度：只有一个for循环，所以时间复杂度为O(n)

空间复杂度：O(1)

思路二：动态规划

参考：https://leetcode-cn.com/problems/palindromic-substrings/solution/shou-hua-tu-jie-dong-tai-gui-hua-si-lu-by-hyj8/

动态规划，二维数组，dp[i][j]是个布尔值，表示[i, j]之间的子串是否是回文串

区间只有一个字符肯定是回文串

区间只有两个字符，且两个字符相等，那也是回文串

如果[i,j]两个端点的字符相等且内部子串dp[i+1][j-1]也是回文串，那整个区间都是回文串

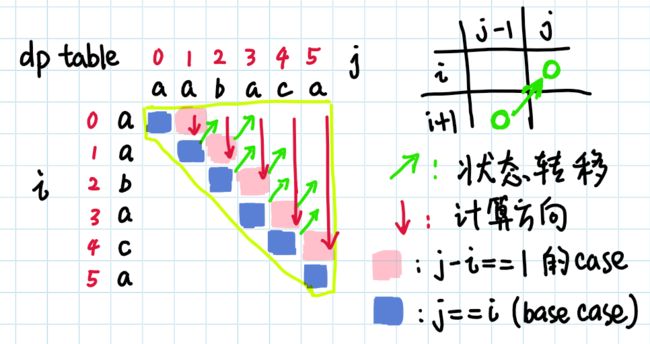
其实上面三种情况可以归纳为，如果区间两端字符相等，且区间长度小于等于2或者大于2但是内部是回文串，那么整个区间都是回文串，借用上面参考文章作者的一张图

 

因为转态转移方程中求dp[i][j]时用到了dp[i+1][j-1], 所以我们的外层循环应该循环j, 当前 j 把内层循环的的所有 i 都迭代一遍，这样dp[i][j]使用dp[i+1][j-1]就没有问题了

 1 class Solution {
 2     public String longestPalindrome(String s) {
 3         // 动态规划
 4         if(s == null){
 5             return null;
 6         }
 7         int maxLength = 0;      // 当前回文子串的最大长度
 8         String maxPalindrome = "";
 9         int len = s.length();
10         boolean[][] dp = new boolean[len][len]; // 保存[i, j]区间的子串是否为回文子串
11         for(int j = 0; j < len; j++){
12             for(int i = 0; i <= j; i++){
13                 if(s.charAt(i) == s.charAt(j) && (j - i <= 1 || dp[i+1][j-1])){
14                     dp[i][j] = true;
15                     if(maxLength < j - i + 1){
16                         maxLength = j - i + 1;
17                         maxPalindrome = s.substring(i, j+1);
18                     }
19                 }
20             }
21         }
22         return maxPalindrome;
23     }
24 }

leetcode 执行用时：257 ms > 11.41%, 内存消耗：45.1 MB > 5.76%, 比思路一慢了很多，多了空间，也多了时间

复杂度分析：

时间复杂度：两个for循环， 所以空间复杂度为O(n²)

空间复杂度：需要一个n* n的矩阵，所以空间复杂度为O(n²)

空间降维

 1 class Solution {
 2     public String longestPalindrome(String s) {
 3         // 动态规划
 4         if(s == null){
 5             return null;
 6         }
 7         int maxLength = 0;      // 当前回文子串的最大长度
 8         String maxPalindrome = "";
 9         int len = s.length();
10         boolean[] dp = new boolean[len]; // 保存[i, j]区间的子串是否为回文子串
11         for(int j = 0; j < len; j++){
12             for(int i = 0; i <= j; i++){
13                 if(s.charAt(i) == s.charAt(j) && (j - i <= 1 || dp[i+1])){
14                     dp[i] = true;
15                     if(maxLength < j - i + 1){
16                         maxLength = j - i + 1;
17                         maxPalindrome = s.substring(i, j+1);
18                     }
19                 }else{
20                     dp[i] = false;
21                 }
22             }
23         }
24         return maxPalindrome;
25     }
26 }

leetcode 执行用时：247 ms > 11.58%, 内存消耗：39.2 MB > 54.45%, 时间效率基本没变，但是空间效率提升了很多

复杂度分析：

时间复杂度：两个循环，遍历了 len * len /2个元素，所以时间复杂度为O(n ²)

空间复杂度：只需要一个长度为 n的矩阵，所以空间复杂度为O(n)