距离度量 —— 曼哈顿距离(Manhattan Distance)
Python学习系列文章: 目录
![]()
文章目录
- 一、概述
- 二、计算公式
- ① 二维平面上的曼哈顿距离
- ② 三维空间上的曼哈顿距离
- ③ n维空间上的曼哈顿距离
一、概述
曼哈顿街区熙熙攘攘,在高处向下望去,曼哈顿的建筑方方正正地排列在一条条街道上,仿佛一个个棋子排列在键盘上。

想要计算两个建筑之间的距离,我们不能横穿某个建筑,需要拐弯抹角,经过一个个十字路口,才能到达我们想要去的地方。

曼哈顿距离,也正是这个原理,不能像 绿线(/) 一样,横穿建筑,而是需要和其它三条线一样, 穿过大街小巷。
二、计算公式
① 二维平面上的曼哈顿距离
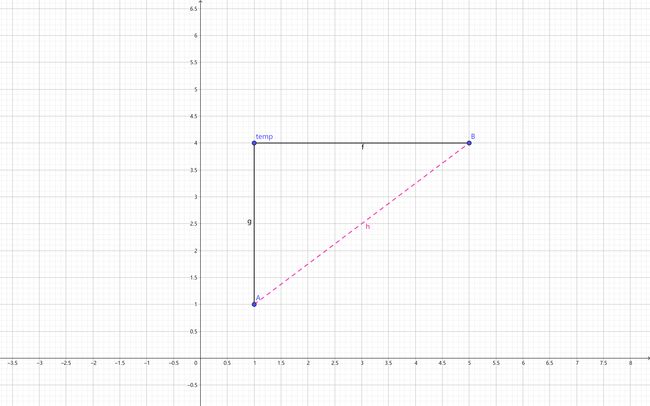
假设 二维平面 内有两点: a ( x 1 , y 1 ) a(x_{1},y_{1}) a(x1,y1) 与 b ( x 2 , y 2 ) b(x_{2},y_{2}) b(x2,y2)
则二维平面的曼哈顿距离公式为:
d 12 = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ d_{12}=|x_{1}-x_{2}|+|y_{1}-y_{2}| d12=∣x1−x2∣+∣y1−y2∣
例如上图的 A ( 1 , 1 ) A(1,1) A(1,1) 与 B ( 5 , 4 ) B(5,4) B(5,4),则 A B AB AB 两点的距离为:
d A B = ∣ 5 − 1 ∣ + ∣ 4 − 1 ∣ = 4 + 3 = 7 \begin{aligned} d_{AB} &=|5-1|+|4-1| \\ &=4+3\\ &=7 \end{aligned} dAB=∣5−1∣+∣4−1∣=4+3=7
② 三维空间上的曼哈顿距离
假设 三维空间 内有两点: a ( x 1 , y 1 , z 1 ) a(x_{1},y_{1},z_{1}) a(x1,y1,z1) 与 b ( x 2 , y 2 , z 2 ) b(x_{2},y_{2},z_{2}) b(x2,y2,z2)
则三维空间的距离公式为:
d 12 = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ + ∣ z 1 − z 2 ∣ d_{12}=|x_{1}-x_{2}|+|y_{1}-y_{2}|+|z_{1}-z_{2}| d12=∣x1−x2∣+∣y1−y2∣+∣z1−z2∣
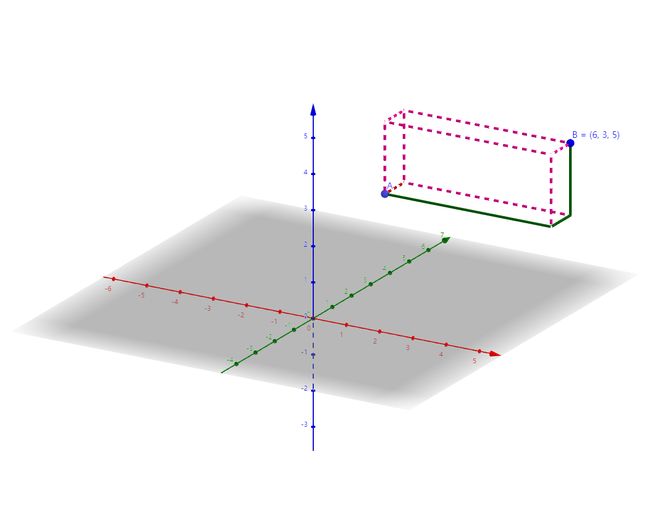
举个例子,比如上图的 A ( 1 , 2 , 3 ) A(1,2,3) A(1,2,3) 与 B ( 6 , 3 , 5 ) B(6,3,5) B(6,3,5) 两点,计算 A B AB AB 两点的曼哈顿距离为:
d A B = ∣ 6 − 1 ∣ + ∣ 3 − 2 ∣ + ∣ 5 − 3 ∣ = 5 + 1 + 2 = 8 \begin{aligned} d_{AB} &=|6-1|+|3-2|+|5-3| \\ &=5+1+2\\ &=8 \end{aligned} dAB=∣6−1∣+∣3−2∣+∣5−3∣=5+1+2=8
③ n维空间上的曼哈顿距离
假设 n维空间 内有两点: a ( x 11 , x 12 , . . . , x 1 n ) a(x_{11},x_{12},...,x_{1n}) a(x11,x12,...,x1n) 与 b ( x 21 , y 22 , . . . , z 2 n ) b(x_{21},y_{22},...,z_{2n}) b(x21,y22,...,z2n)
则n维空间的距离公式为:
d 12 = ∑ k = 1 n ∣ x 1 k − x 2 k ∣ d_{12}=\sum_{k=1}^n|x_{1k}-x_{2k}| d12=k=1∑n∣x1k−x2k∣
![]()