NEUQACM双周赛（五）

L1-1 计算摄氏温度（C++）

本题要求编写程序，计算华氏温度$100°F$对应的摄氏温度。计算公式：$C=5\times (F-32)/9$，式中：$C$表示摄氏温度，$F$表示华氏温度，输出数据要求为整型。

输入格式:

本题目没有输入。

输出格式:

按照下列格式输出

fahr = 100, celsius = 计算所得摄氏温度的整数值

解题思路：

签到$qwq$

#include 
using namespace std;

int main() {
	int f = 100;
	int c = 5 * (f - 32) / 9;
	cout << "fahr = 100, celsius = " << c << endl;
	return 0;
}

L1-2 查验身份证（C++，模拟）

一个合法的身份证号码由$17$位地区、日期编号和顺序编号加$1$位校验码组成。校验码的计算规则如下：

首先对前$17$位数字加权求和，权重分配为：$\{7,9,10,5,8,4,2,1,6,3,7,9,10,5,8,4,2\}$；然后将计算的和对$11$取模得到值Z；最后按照以下关系对应Z值与校验码M的值：

Z：0 1 2 3 4 5 6 7 8 9 10
M：1 0 X 9 8 7 6 5 4 3 2

现在给定一些身份证号码，请你验证校验码的有效性，并输出有问题的号码。

输入格式：

输入第一行给出正整数$N$（$\le 100$）是输入的身份证号码的个数。随后$N$行，每行给出$1$个$18$位身份证号码。

输出格式：

按照输入的顺序每行输出$1$个有问题的身份证号码。这里并不检验前$17$位是否合理，只检查前$17$位是否全为数字且最后$1$位校验码计算准确。如果所有号码都正常，则输出All passed。

输入样例1：

4
320124198808240056
12010X198901011234
110108196711301866
37070419881216001X

输出样例1：

12010X198901011234
110108196711301866
37070419881216001X

输入样例2：

2
320124198808240056
110108196711301862

输出样例2：

All passed

解题思路：

根据题目提供的流程用代码模拟就可以了：

首先读入一个字符串，对于一个合法的身份证号码，前十七位应该为数字，最后一位是检验和

我们的检验流程就是：对前十七位数字加权求和，然后与最后一位相比较

鉴于可能有人不知道什么是加权，这里简单说明一下

对于十进制整数$1324$来说，$1$的权重就是$1000$，$3$的权重就是$100$，依此类推

注意需要将检验和字符转换为其代表的数字

最后，AC代码如下

#include 
#include 
using namespace std;
const int mod_num = 11;
const int max_n = 100;

const int power[17] = { 7,9,10,5,8,4,2,1,6,3,7,9,10,5,8,4,2 };
const char check[12] = "10X98765432";

int main() {
	int n, sum = 0;
	cin >> n;
	for (int i = 0; i < n; i++) {
		string str;
		cin >> str;
		int z = 0;
		bool res = true;
		for (int i = 0; i < 17; i++) {
			if ('0' <= str[i] && str[i] <= '9')
				z += (str[i] - '0') * power[i];
			else {
				res = false;
				break;
			}
		}
		z %= mod_num;
		
		if (res) res = (check[z] == str[17]);		
		if (!res) {
			sum++;
			cout << str << endl;		
		}
	}
	
	if (!sum) cout << "All passed" << endl;
	return 0;
}

L1-3 帅到没朋友（C++，模拟）

当芸芸众生忙着在朋友圈中发照片的时候，总有一些人因为太帅而没有朋友。本题就要求你找出那些帅到没有朋友的人。

输入格式：

输入第一行给出一个正整数N（$\le 100$），是已知朋友圈的个数；随后N行，每行首先给出一个正整数K（$\le 1000$），为朋友圈中的人数，然后列出一个朋友圈内的所有人——为方便起见，每人对应一个ID号，为$5$位数字（从$00000$到$99999$），$ID$间以空格分隔；之后给出一个正整数M（$\le 10000$），为待查询的人数；随后一行中列出M个待查询的$ID$，以空格分隔。

注意：没有朋友的人可以是根本没安装“朋友圈”，也可以是只有自己一个人在朋友圈的人。虽然有个别自恋狂会自己把自己反复加进朋友圈，但题目保证所有K超过$1$的朋友圈里都至少有$2$个不同的人。

输出格式：

按输入的顺序输出那些帅到没朋友的人。$ID$间用$1$个空格分隔，行的首尾不得有多余空格。如果没有人太帅，则输出No one is handsome。

注意：同一个人可以被查询多次，但只输出一次。

输入样例1：

3
3 11111 22222 55555
2 33333 44444
4 55555 66666 99999 77777
8
55555 44444 10000 88888 22222 11111 23333 88888

输出样例1：

10000 88888 23333

输入样例2：

3
3 11111 22222 55555
2 33333 44444
4 55555 66666 99999 77777
4
55555 44444 22222 11111

输出样例2：

No one is handsome

解题思路：

前排提示：输出格式要求行尾不能有多余空格，注意特殊处理

首先来理解一下题意：

题目给出若干个朋友圈，每个朋友圈内有若干个人，一个人很帅，当且仅当他没有出现在任何朋友圈内，或者他出现的朋友圈只有他自己一个人

接下来用代码进行模拟

哪有什么算法啊（战术后仰）

对于题目的查询，我们只需要辨别出这个人到底帅不帅就行了

而根据题目的输入格式，显然维护不帅的人的集合相对容易一些

利用STL的set，我们将所有人数多于$1$的朋友圈内的人插入集合进行维护

最后由于要求按查询顺序输出，并且可能多次查询同一个人

所以我们需要维护一个答案数组

因为数据比较水，我们采用暴力方法去重，即把所有已经出现过的人放入另外一个set维护

如果没有出现过，我们将其推入一个vector容器中（不能用set，因为集合具有无序性）

AC代码如下

#include 
#include 
#include 
#include  
using namespace std;
const int max_n = 100;
const int max_k = 1000;
const int max_m = 10000;

set<string>s, ans;
vector<string>v;

int main() {
	int n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		int k;
		cin >> k;
		string str;
		if (k == 1) cin >> str;
		else {
			for (int j = 0; j < k; j++) {
				cin >> str;
				s.insert(str);	
			}
		}
	}
	
	int m;
	cin >> m;
	for (int i = 0; i < m; i++) {
		string str;
		cin >> str;
		int ret = s.count(str);
		if (!ret && !ans.count(str)) {
			ans.insert(str);
			v.push_back(str);
		} 
	}
	
	if (v.empty()) cout << "No one is handsome" << endl;
	else{
		string buffer = "";
		for (vector<string>::iterator iter = v.begin(); iter != v.end(); iter++) {
			if (buffer != "") {
				cout << buffer << ' ';
			}
			buffer = *iter;
		}
		cout << buffer << endl;
	}
	return 0;
}

L1-4 输出GPLT（C++，字符串）

给定一个长度不超过$10000$的、仅由英文字母构成的字符串。请将字符重新调整顺序，按GPLTGPLT....这样的顺序输出，并忽略其它字符。当然，四种字符（不区分大小写）的个数不一定是一样多的，若某种字符已经输出完，则余下的字符仍按GPLT的顺序打印，直到所有字符都被输出。

输入格式：

输入在一行中给出一个长度不超过$10000$的、仅由英文字母构成的非空字符串。

输出格式：

在一行中按题目要求输出排序后的字符串。题目保证输出非空。

输入样例：

pcTclnGloRgLrtLhgljkLhGFauPewSKgt

输出样例：

GPLTGPLTGLTGLGLL

解题思路：

遍历读入的字符串，统计其中GPTL字符的个数（注意不分大小写）

for (int i = 0; i < len; i++) {
	switch(str[i]) {
		case 'G':
		case 'g':
			sum[0]++;
			break;
		case 'P':
		case 'p':
			sum[1]++;
			break;
		case 'L': 
		case 'l':
			sum[2]++;
			break;
		case 'T':
		case 't':
			sum[3]++;
			break;
		default:
			break;
	}
}

然后遍历输出，直到没有字符为止

while (sum[0] || sum[1] || sum[2] || sum[3]) {
	for (int i = 0; i < 4; i++) {
		if (sum[i]) {
			sum[i]--;
			cout << cs[i];
		}
	}
}

AC代码如下

#include 
#include  
using namespace std;
const int max_len = 10000;

int sum[4];
char cs[5] = "GPLT";

int main() {
	string str;
	cin >> str;
	int len = str.size();
	for (int i = 0; i < len; i++) {
		switch(str[i]) {
			case 'G':
			case 'g':
				sum[0]++;
				break;
			case 'P':
			case 'p':
				sum[1]++;
				break;
			case 'L': 
			case 'l':
				sum[2]++;
				break;
			case 'T':
			case 't':
				sum[3]++;
				break;
			default:
				break;
		}
	}
	
	while (sum[0] || sum[1] || sum[2] || sum[3]) {
		for (int i = 0; i < 4; i++) {
			if (sum[i]) {
				sum[i]--;
				cout << cs[i];
			}
		}
	}
	return 0;
}

L1-5 判断素数（C++，数学）

本题的目标很简单，就是判断一个给定的正整数是否素数。

输入格式：

输入在第一行给出一个正整数N（$\le 10$），随后N行，每行给出一个小于$2^{31}$的需要判断的正整数。

输出格式：

对每个需要判断的正整数，如果它是素数，则在一行中输出Yes，否则输出No。

输入样例：

2
11
111

输出样例：

Yes
No

解题思路：

首先，我们尝试使用常见的素数判断方法

for (int i = 2; i * i <= num; i++) {
	if (num % i == 0) {
		ans = false;
		break;
	}
}

计算一下时间复杂度$O(10\ast \sqrt{2^{31}})\approx O(10^{5.5})$，是可行的

但是跑起来会$TLE$，为什么呢？

返回题干查看数据范围，发现最大输入是$2^{31}-1$

那么再看一看我们的循环停止条件i * i <= num，我们知道i * i是int类型

但是对于最大输入这个条件不可能为false，因为不可能存在int类型的数据比$2^{31}-1$大，爆精度了

这个$bug$好修，开long long

然后再次提交发现答案错误

$emmm$，再回到题干，发现输入为正整数，也就是说可以输入$1$

对于$1$，我们进行特殊判定即可

最后，AC代码如下

#include 
using namespace std;
const int max_n = 10;
const int max_num = 1 << 31 - 1;

int main() {
	int n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		long long num;
		cin >> num;
        
        if (num == 1) {
            cout << "No" << endl;
            continue;
        }
        
		bool ans = true;
		for (long long j = 2; j * j <= num; j++) {
			if (num % j == 0) {
				ans = false;
				break;
			}
		}
		if (ans) cout << "Yes" << endl;
		else cout << "No" << endl;
	}
	return 0;
}

这里在附加上几个更高效的素数判定方法

（1）比较玄学的判定方法

bool is_prime(int num) {
	if (num <= 3) return num > 1;
	if (num % 6 != 1 && num % 6 != 5) return false;

	for (int i = 5; i * i <= num; i += 6)
		if (num % i == 0 || num % (i + 2) == 0)
			return false;
	return true;
}

（2）费马小定理：

在$modp$意义下，如果$p$为质数并且$b$不是$p$的倍数

则有$b^{p-1}modp\equiv 1$

#include 
using namespace std;

long long quick_expo(long long a, long long b, long long mod_num) {
	/* 快速幂 */
	long long ret = 1;
	while (b != 1) {
		if (b & 1) ret = (ret * a) % mod_num;
		a = (a * a) % mod_num;
		b >>= 1;
	}
	return (ret * a) % mod_num;
}

int main() {
	int n;
	long long a = 2;
	cin >> n;
	for (int i = 0; i < n; i++) {
		long long num;
		cin >> num;
		if (num == 2) {
			cout << "Yes" << endl;
			continue;
		}
		if (num == 1) {
			cout << "No" << endl;
			continue;
		}
		if (a * quick_expo(a, num - 2, num) % num == 1) cout << "Yes" << endl;
		else cout << "No" << endl;
	}
	return 0;
}

L1-6 最佳情侣身高差（C++，模拟）

专家通过多组情侣研究数据发现，最佳的情侣身高差遵循着一个公式：（女方的身高）$\times 1.09=$（男方的身高）。如果符合，你俩的身高差不管是牵手、拥抱、接吻，都是最和谐的差度。

下面就请你写个程序，为任意一位用户计算他$/$她的情侣的最佳身高。

输入格式：

输入第一行给出正整数$N$（$\le 10$），为前来查询的用户数。随后$N$行，每行按照“性别 身高”的格式给出前来查询的用户的性别和身高，其中“性别”为“$F$”表示女性、“$M$”表示男性；“身高”为区间 $[1.0,3.0]$ 之间的实数。

输出格式：

对每一个查询，在一行中为该用户计算出其情侣的最佳身高，保留小数点后2位。

输入样例：

2
M 1.75
F 1.8

输出样例：

1.61
1.96

解题思路：

先根据字符判断性别，然后输出（采用iomanip控制输出精度）：

（1）$M:$输出为输入 / 1.09

（2）$F:$输出为输入 * 1.09

AC代码如下

#include 
#include 
using namespace std;
const int max_n = 10;

int main() {
	int n;
	char sex;
	double height;
	cin >> n;
	cout << setiosflags(ios::fixed) << setprecision(2);
	for (int i = 0; i < n; i++) {
		cin >> sex >> height;
		if (sex == 'F') {
			cout << height * 1.09 << endl;
		}
		else {
			cout << height / 1.09 << endl;
		}
	}
	return 0;
}

L1-7 连续因子（C++，数学）

一个正整数 $N$ 的因子中可能存在若干连续的数字。例如 $630$ 可以分解为 $3\times 5\times 6\times 7$，其中 $5$、$6$、$7$ 就是 $3$ 个连续的数字。给定任一正整数 $N$，要求编写程序求出最长连续因子的个数，并输出最小的连续因子序列。

输入格式：

输入在一行中给出一个正整数 $N$（$1<N<2^{31}$）。

输出格式：

首先在第 $1$ 行输出最长连续因子的个数；然后在第 $2$ 行中按 因子1*因子2*……*因子k 的格式输出最小的连续因子序列，其中因子按递增顺序输出，$1$ 不算在内。

输入样例：

630

输出样例：

3
5*6*7

解题思路：

想要找出最长的连续因子序列，自然要找出所有的连续因子序列

大致上的思路就是：

（1）先找到一个因子，以此作为起始

（2）接下来不断乘法操作，直到乘积不符合条件

（3）记录结尾数字，找到一个连续因子序列，回到步骤（1）

可行性证明：

如果一个$num$能够分解的最长连续因子序列为$n_1,n_2,...,n_m$，那么必然存在$k=\frac{num}{n_1\ast n_2\ast ...\ast n_m}$，使得$num=n_1\ast n_2\ast ...\ast n_m\ast k$

所以找到的连续因子序列符合题意

代码实现如下

for (i = 2; i * i <= num; i++) {
	if (num % i == 0) {//(1) search for next begin
		sum = 1;
		for (j = i; j * sum <= num; j++) {//(2) extend len
			sum *= j;
			if (num % sum == 0 && j - i + 1 > max_len) {//(3) update
				max_beg = i;
				max_len = j - i + 1;
			}
		}
	}
}

由于数据范围是$1$~$2^{31}$，直接枚举必然$TLE$

所以利用因子一定成对出现的性质，我们只枚举到$\sqrt{2^{31}}$为止

for (i = 2; i * i <= num; i++) {
	...
}

最后，AC代码如下

#include 
#include 
const long long max_num = 1 << 31 - 1;

int main() {
	long long num, sum, i, j, max_len = 0, max_beg = -1;;
	scanf("%lld", &num);

	for (i = 2; i * i <= num; i++) {
		if (num % i == 0) {//(1) search for next begin
			sum = 1;
			for (j = i; j * sum <= num; j++) {//(2) extend len
				sum *= j;
				if (num % sum == 0 && j - i + 1 > max_len) {//(3) update
					max_beg = i;
					max_len = j - i + 1;
				}
			}
		}
	}

	if (max_beg == -1) {
		max_beg = num;
		max_len = 1;
	}

	printf("%lld\n", max_len);
	long long max_end = max_beg + max_len;
	for (i = max_beg; i < max_end; i++) {
		if (i == max_beg) printf("%lld", i);
		else printf("*%lld", i);
	}
	printf("\n");
	return 0;
}

注意要开long long，否则循环部分会因为爆精度无法停止，导致$TLE$

或者输出部分会因为爆精度而导致结果错误

L1-8 出生年（C++，模拟）

以上是新浪微博中一奇葩贴：“我出生于$1988$年，直到$25$岁才遇到$4$个数字都不相同的年份。”也就是说，直到$2013$年才达到“$4$个数字都不相同”的要求。本题请你根据要求，自动填充“我出生于y年，直到x岁才遇到n个数字都不相同的年份”这句话。

输入格式：

输入在一行中给出出生年份y和目标年份中不同数字的个数n，其中y在$[1,3000]$之间，n可以是$2$、或$3$、或$4$。注意不足$4$位的年份要在前面补零，例如公元$1$年被认为是$0001$年，有$2$个不同的数字$0$和$1$。

输出格式：

根据输入，输出x和能达到要求的年份。数字间以$1$个空格分隔，行首尾不得有多余空格。年份要按$4$位输出。注意：所谓“n个数字都不相同”是指不同的数字正好是n个。如“$2013$”被视为满足“$4$位数字都不同”的条件，但不被视为满足$2$位或$3$位数字不同的条件。

输入样例1：

1988 4

输出样例1：

25 2013

输入样例2：

1 2

输出样例2：

0 0001

解题思路：

数据范围很小，直接枚举就可以

判定是否满足条件，这里采用维护一个bool数组的方法

每轮重新记录出现过的数字，然后对数组求和

AC代码如下

#include 
#include 
#include 
using namespace std;

char year[5] = "0000";
bool arr[10];

inline void tostring(int y) {
	/* 转为字符串 */
	int t, i = 3;
	while (y) {
		t = y % 10;
		y /= 10;

		year[i--] = char(t + '0');
	}
}

inline int accumulate(bool* beg, bool* end) {
	/* 求和 */
	int sum = 0;
	while (beg != end) {
		sum += *beg;
		beg++;
	}
	return sum;
}

int main() {
	int y, n;
	cin >> y >> n;
	tostring(y);
	int x = 0;
	while (true) {
		memset(arr, false, sizeof(bool) * 10);//初始化 
		for (int i = 0; i < 4; i++) {
			arr[year[i] - '0'] = true;
		}

		if (accumulate(arr, arr + 10) == n) {//结束 
			cout << x << ' ' << year << endl;
			break;
		}

		//下一轮 
		year[3]++;
		if (year[3] > '9') {
			year[2]++;
			year[3] = '0';
			if (year[2] > '9') {
				year[1]++;
				year[2] = '0';
				if (year[1] > '9') {
					year[0]++;
					year[1] = '0';
				}
			}
		}
		x++;
	}
	return 0;
}

L2-1 红色警报（C++，并查集）

战争中保持各个城市间的连通性非常重要。本题要求你编写一个报警程序，当失去一个城市导致国家被分裂为多个无法连通的区域时，就发出红色警报。注意：若该国本来就不完全连通，是分裂的$k$个区域，而失去一个城市并不改变其他城市之间的连通性，则不要发出警报。

输入格式：

输入在第一行给出两个整数N（$0<N\le 500$）和M（$\le 5000$），分别为城市个数（于是默认城市从$0$到N-1编号）和连接两城市的通路条数。随后M行，每行给出一条通路所连接的两个城市的编号，其间以$1$个空格分隔。在城市信息之后给出被攻占的信息，即一个正整数K和随后的K个被攻占的城市的编号。

注意：输入保证给出的被攻占的城市编号都是合法的且无重复，但并不保证给出的通路没有重复。

输出格式：

对每个被攻占的城市，如果它会改变整个国家的连通性，则输出Red Alert: City k is lost!，其中k是该城市的编号；否则只输出City k is lost.即可。如果该国失去了最后一个城市，则增加一行输出Game Over.。

输入样例：

5 4
0 1
1 3
3 0
0 4
5
1 2 0 4 3

输出样例：

City 1 is lost.
City 2 is lost.
Red Alert: City 0 is lost!
City 4 is lost.
City 3 is lost.
Game Over.

解题思路：

整张图具有若干子图，每个子图均是一个强连通分量

对于强连通分量，我们常常采用并查集维护

国家的连通性改变是指一个集合分裂为两个集合

也就是说，失去一个城市之后，如果强连通分量的数量减少（即一个区域被完全攻占），国家的连通性不会发生改变。

每失去一个城市，因为图发生变化，我们都必须重新生成集合，然后计算强连通分量的数目

以上是整体的思路，接下来实现代码

考虑到重新生成集合需要反复利用边的数据，所以将其存储在数组中

for (int i = 0; i < m; i++) {
	cin >> edges[i].u >> edges[i].v;
}

对于失去的城市，我们采用bool数组进行标记

cin >> k;
for (int i = 0; i < k; i++) {
	cin >> city;
	lose[i] = true;
	...
}

每失去一座城市，我们都需要重新统计强连通分量的数目，然后与失去前比较，判断如何输出

cin >> k;
for (int i = 0; i < k; i++) {
	cin >> city;
	lose[city] = true;
	cur = count_submap(n, m);//统计子图数量
	if (cur > last)//连通性改变
		cout << "Red Alert: City " << city << " is lost!" << endl;
	else//连通性不变
		cout << "City " << city << " is lost." << endl;
	last = cur;
}

最后就是本题的关键，count_submap函数的实现

首先我们需要重新生成集合

void init(int n, int m) {
    /* 重新生成集合 */
	for (int i = 0; i < n; i++) fa[i] = i;

	for (int i = 0; i < m; i++) {
		int u = edges[i].u, v = edges[i].v;
		if (!lose[u] && !lose[v] && !is_insame(u, v))
            //如果两个城市均未失去，并且尚未合并到一个集合中
            merge(u, v);
	}
}

然后统计集合，也就是强连通分量的数目

int sum = 0;
for (int i = 0; i < n; i++) {
	if (!lose[i] && i == fa[i]) sum++;
}

最后组合在一起

int count_submap(int n, int m) {
	/* 统计强连通分量数目 */
	init(n, m);

	int sum = 0;
	for (int i = 0; i < n; i++) {
		if (!lose[i] && i == fa[i]) sum++;
	}
	return sum;
}

代码实现结束，AC代码如下

#include 
using namespace std;
const int max_n = 500;
const int max_m = 5000;

int fa[max_n];
bool lose[max_n];
struct edge { int u, v; }edges[max_m];

int find(int x) {
	return x == fa[x] ? x : (fa[x] = find(fa[x]));
}

bool is_insame(int x, int y) {
	x = find(x); y = find(y);
	return x == y;
}

void merge(int x, int y) {
	x = find(x); y = find(y);
	fa[x] = y;
}

void init(int n, int m) {
	for (int i = 0; i < n; i++) fa[i] = i;

	for (int i = 0; i < m; i++) {
		int u = edges[i].u, v = edges[i].v;
		if (!lose[u] && !lose[v] && !is_insame(u, v)) merge(u, v);
	}
}

int count_submap(int n, int m) {
	init(n, m);

	int sum = 0;
	for (int i = 0; i < n; i++) {
		if (!lose[i] && i == fa[i]) sum++;
	}
	return sum;
}

int main() {
	int n, m;
	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		cin >> edges[i].u >> edges[i].v;
	}

	int k, city, cur, last = count_submap(n, m);
	cin >> k;
	for (int i = 0; i < k; i++) {
		cin >> city;
		lose[city] = true;
		cur = count_submap(n, m);
		if (cur > last) 
			cout << "Red Alert: City " << city << " is lost!" << endl;
		else 
			cout << "City " << city << " is lost." << endl;

		last = cur;
	}
	if (k == n) {
		cout << "Game Over." << endl;
	}
	return 0;
}

L2-2 秀恩爱分得快（C++，模拟）

古人云：秀恩爱，分得快。

互联网上每天都有大量人发布大量照片，我们通过分析这些照片，可以分析人与人之间的亲密度。如果一张照片上出现了 $K$ 个人，这些人两两间的亲密度就被定义为 $1/K$。任意两个人如果同时出现在若干张照片里，他们之间的亲密度就是所有这些同框照片对应的亲密度之和。下面给定一批照片，请你分析一对给定的情侣，看看他们分别有没有亲密度更高的异性朋友？

输入格式：

输入在第一行给出 $2$ 个正整数：$N$（不超过$1000$，为总人数——简单起见，我们把所有人从 $0$ 到 $N-1$ 编号。为了区分性别，我们用编号前的负号表示女性）和 $M$（不超过$1000$，为照片总数）。随后 $M$ 行，每行给出一张照片的信息，格式如下：

K P[1] ... P[K]

其中 $K$（$\le 500$）是该照片中出现的人数，$P[1]$ ~ $P[K]$ 就是这些人的编号。最后一行给出一对异性情侣的编号 $A$ 和 $B$。同行数字以空格分隔。题目保证每个人只有一个性别，并且不会在同一张照片里出现多次。

输出格式：

首先输出 A PA，其中 PA 是与 A 最亲密的异性。如果 PA 不唯一，则按他们编号的绝对值递增输出；然后类似地输出 B PB。但如果 A 和 B 正是彼此亲密度最高的一对，则只输出他们的编号，无论是否还有其他人并列。

输入样例 1：

10 4
4 -1 2 -3 4
4 2 -3 -5 -6
3 2 4 -5
3 -6 0 2
-3 2

输出样例 1：

-3 2
2 -5
2 -6

输入样例 2：

4 4
4 -1 2 -3 0
2 0 -3
2 2 -3
2 -1 2 
-3 2

输出样例 2：

-3 2

解题思路：

本题是一道非常折磨的模拟题

首先我们来模拟数据的输入

但凡索引不是以$0$开头，或者输入是性别和编号分开输入，我们就不需要把输入视为字符串

因为$-0$的存在，输入需要按字符串处理

关系是双向的，我们采用二维数组来模拟

由于亲密度计算公式是$1/K$，数组应该是double类型

然后我们来寻找最大亲密度

对于异性的判定，我们采用异或操作^

然后是由于double类型产生的一些问题

我们不能简单用num1 > num2来比较两个浮点数的大小关系，也不能用num1 == num2来判断两个浮点数是否相等

因为浮点数是近似的，会发生截断

要想判断num1 > num2，我们采用num1 - num2 > 1e-6

要想判断num1 == num2，我们采用fabs(num1 - num2) < 1e-6

最后是数据的输出

我们采用format + printf来格式化输出

但记得如果这对情侣互为最亲密的人，我们只需要输出他们的编号

如果不是的情况下，也不要忘记按编号绝对值升序输出并列的人

最后，AC代码如下

#include 
#include 
#include 
#include 
using namespace std;
const int max_n = 1000;
const int max_m = 1000;

double relation[max_n][max_n];
bool sex[max_n];
int input[max_n];

int str2int(string str) {
	int len = str.size();
	int b = 1, i = 0;
	if (str[0] == '-') {
		b = 0;
		i++;
	}

	int ret = 0;
	while (i < len) {
		ret = ret * 10 + (str[i] - '0');
		i++;
	}
	sex[ret] = b;
	return ret;
}

void str2char(string str, char* ch) {
	int len = str.size();
	for (int i = 0; i < len; i++) {
		ch[i] = str[i];
	}
	ch[len] = '\0';
}

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	int n, m, k;
	cin >> n >> m;
	string s;

	for (int i = 0; i < m; i++) {
		cin >> k;
		for (int j = 0; j < k; j++) {
			cin >> s;
			input[j] = str2int(s);
		}
		//统计亲密度
		for (int j = 0; j < k; j++) {
			for (int z = j + 1; z < k; z++) {
				relation[input[j]][input[z]] += 1.0 / k;
				relation[input[z]][input[j]] += 1.0 / k;
			}
		}
	}

	string p1, p2;
	int ip1, ip2;
	vector<pair<double, int>>ans1, ans2;//最大亲密度
	
	cin >> p1 >> p2;
	ip1 = str2int(p1); ip2 = str2int(p2);
	double t = relation[ip1][ip2];//情侣亲密度
	ans1.push_back({ t,ip2 }); ans2.push_back({ t,ip1 });
	
	//寻找最大亲密度
	for (int i = 0; i < n; i++) {
		if (i != ip2 && sex[i] ^ sex[ip1]) {
			if (relation[ip1][i] - ans1[0].first > 1e-6) {
				ans1.clear();
				ans1.push_back({ relation[ip1][i],i });
			}
			else if (fabs(ans1[0].first - relation[ip1][i]) < 1e-6) {
				ans1.push_back({ relation[ip1][i],i });
			}
		}
		if (i != ip1 && sex[i] ^ sex[ip2]) {
			if (relation[ip2][i] - ans2[0].first > 1e-6) {
				ans2.clear();
				ans2.push_back({ relation[ip2][i],i });
			}
			else if (fabs(ans2[0].first - relation[ip2][i]) < 1e-6) {
				ans2.push_back({ relation[ip2][i],i });
			}
		}
	}

	char format[1024];//输出格式
	string temp;
	
	if (sex[ip1]) temp = "%d -%d\n";
	else temp = "-%d %d\n";
	str2char(temp, format);

	if (ans1[0].second == ip2 && ans2[0].second == ip1) {
		printf(format, ip1, ip2);
		return 0;
	}
	
	{
		sort(ans1.begin(), ans1.end(), [](pair<double, int>p1, pair<double, int>p2) {
			return p1.second < p2.second;
			});
		int len = ans1.size();
		for (int i = 0; i < len; i++) {
			printf(format, ip1, ans1[i].second);
		}
	}

	if (sex[ip2]) temp = "%d -%d\n";
	else temp = "-%d %d\n";
	str2char(temp, format);
		
	{
		sort(ans2.begin(), ans2.end(), [](pair<double, int>p1, pair<double, int>p2) {
			return p1.second < p2.second;
			});
		int len = ans2.size();
		for (int i = 0; i < len; i++) {
			printf(format, ip2, ans2[i].second);
		}
	}
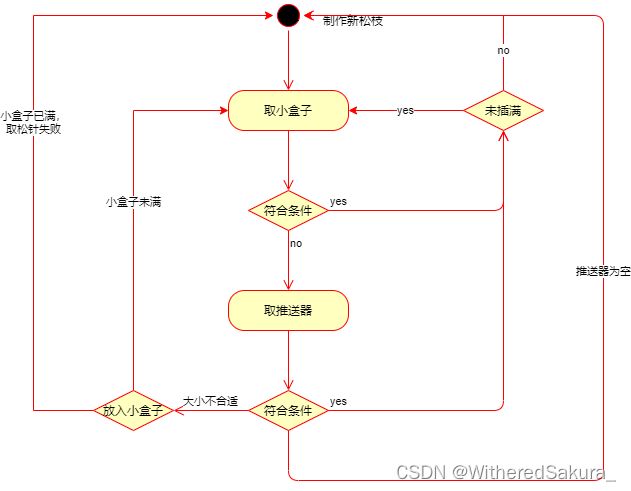
	return 0;
}

L2-3 插松枝（C++，模拟）

人造松枝加工场的工人需要将各种尺寸的塑料松针插到松枝干上，做成大大小小的松枝。他们的工作流程（并不）是这样的：

• 每人手边有一只小盒子，初始状态为空。
• 每人面前有用不完的松枝干和一个推送器，每次推送一片随机型号的松针片。
• 工人首先捡起一根空的松枝干，从小盒子里摸出最上面的一片松针 —— 如果小盒子是空的，就从推送器上取一片松针。将这片松针插到枝干的最下面。
• 工人在插后面的松针时，需要保证，每一步插到一根非空松枝干上的松针片，不能比前一步插上的松针片大。如果小盒子中最上面的松针满足要求，就取之插好；否则去推送器上取一片。如果推送器上拿到的仍然不满足要求，就把拿到的这片堆放到小盒子里，继续去推送器上取下一片。注意这里假设小盒子里的松针片是按放入的顺序堆叠起来的，工人每次只能取出最上面（即最后放入）的一片。
• 当下列三种情况之一发生时，工人会结束手里的松枝制作，开始做下一个：

（1）小盒子已经满了，但推送器上取到的松针仍然不满足要求。此时将手中的松枝放到成品篮里，推送器上取到的松针压回推送器，开始下一根松枝的制作。

（2）小盒子中最上面的松针不满足要求，但推送器上已经没有松针了。此时将手中的松枝放到成品篮里，开始下一根松枝的制作。

（3）手中的松枝干上已经插满了松针，将之放到成品篮里，开始下一根松枝的制作。

现在给定推送器上顺序传过来的 $N$ 片松针的大小，以及小盒子和松枝的容量，请你编写程序自动列出每根成品松枝的信息。

输入格式：

输入在第一行中给出 $3$ 个正整数：$N$（$\le 10^3$），为推送器上松针片的数量；$M$（$\le 20$）为小盒子能存放的松针片的最大数量；$K$（$\le 5$）为一根松枝干上能插的松针片的最大数量。

随后一行给出 $N$ 个不超过 $100$ 的正整数，为推送器上顺序推出的松针片的大小。

输出格式：

每支松枝成品的信息占一行，顺序给出自底向上每片松针的大小。数字间以 1 个空格分隔，行首尾不得有多余空格。

输入样例：

8 3 4
20 25 15 18 20 18 8 5

输出样例：

20 15
20 18 18 8
25 5

解题思路：

没有算法，全是模拟

解题关键就是清晰了解流程，所以我把它画成图放在这里

AC代码如下

#include 
#include 
#include 
#include 
using namespace std;
const int max_n = 1e3;
const int max_m = 20;
const int max_k = 5;
const int NaN = 0x3F3F3F3F;

queue<int>pusher;
stack<int>box;
vector<vector<int>>products;

int main() {
	int n, m, k;
	cin >> n >> m >> k;
	int s;
	for (int i = 0; i < n; i++) {
		cin >> s;
		pusher.push(s);
	}

	vector<int>temp;
	while (!(pusher.empty() && box.empty())) {
		temp.push_back(NaN);
		while (true) {
			if (temp.size() == k + 1) break;

			if (!box.empty() && box.top() <= temp[temp.size() - 1]) {
				int next = box.top(); box.pop();
				temp.push_back(next);
			}
			else if (!pusher.empty() && pusher.front() <= temp[temp.size() - 1]) {
				int next = pusher.front(); pusher.pop();
				temp.push_back(next);
			}
			else if (pusher.empty()) break;
			else {
				if (box.size() < m) {
					int next = pusher.front(); pusher.pop();
					box.push(next);
				}
				else break;
			}
		}
		products.push_back(temp);
		temp.clear();
	}

	for (int i = 0; i < products.size(); i++) {
		for (vector<int>::iterator it = products[i].begin(); it != products[i].end(); it++) {
			if (it == products[i].begin()) cout << *(++it);
			else cout << ' ' << *it;
		}
		cout << endl;
	}
	return 0;
}

L2-4 哲哲打游戏（C++，模拟）

哲哲是一位硬核游戏玩家。最近一款名叫《达诺达诺》的新游戏刚刚上市，哲哲自然要快速攻略游戏，守护硬核游戏玩家的一切！

为简化模型，我们不妨假设游戏有 $N$ 个剧情点，通过游戏里不同的操作或选择可以从某个剧情点去往另外一个剧情点。此外，游戏还设置了一些存档，在某个剧情点可以将玩家的游戏进度保存在一个档位上，读取存档后可以回到剧情点，重新进行操作或者选择，到达不同的剧情点。

为了追踪硬核游戏玩家哲哲的攻略进度，你打算写一个程序来完成这个工作。假设你已经知道了游戏的全部剧情点和流程，以及哲哲的游戏操作，请你输出哲哲的游戏进度。

输入格式：

输入第一行是两个正整数 $N$ 和 $M$ ($1\le N,M\le 10^5$)，表示总共有 $N$ 个剧情点，哲哲有 $M$ 个游戏操作。

接下来的 $N$ 行，每行对应一个剧情点的发展设定。第 $i$ 行的第一个数字是 $K_i$，表示剧情点 $i$ 通过一些操作或选择能去往下面 $K_i$ 个剧情点；接下来有 $K_i$ 个数字，第 $k$ 个数字表示做第 $k$ 个操作或选择可以去往的剧情点编号。

最后有 $M$ 行，每行第一个数字是 $0$、$1$ 或 $2$，分别表示：

• $0$ 表示哲哲做出了某个操作或选择，后面紧接着一个数字 $j$，表示哲哲在当前剧情点做出了第 $j$ 个选择。我们保证哲哲的选择永远是合法的。
• $1$ 表示哲哲进行了一次存档，后面紧接着是一个数字 $j$，表示存档放在了第 $j$ 个档位上。
• $2$ 表示哲哲进行了一次读取存档的操作，后面紧接着是一个数字 $j$，表示读取了放在第 $j$ 个位置的存档。

约定：所有操作或选择以及剧情点编号都从 $1$ 号开始。存档的档位不超过 $100$ 个，编号也从 $1$ 开始。游戏默认从 $1$ 号剧情点开始。总的选项数（即 $\sum K_i$）不超过 $10^6$。

输出格式：

对于每个 $1$（即存档）操作，在一行中输出存档的剧情点编号。

最后一行输出哲哲最后到达的剧情点编号。

输入样例：

10 11
3 2 3 4
1 6
3 4 7 5
1 3
1 9
2 3 5
3 1 8 5
1 9
2 8 10
0
1 1
0 3
0 1
1 2
0 2
0 2
2 2
0 3
0 1
1 1
0 2

输出样例：

1
3
9
10

样例解释：

简单给出样例中经过的剧情点顺序：

$1$ -> $4$ -> $3$ -> $7$ -> $8$ -> $3$ -> $5$ -> $9$ -> $10$。

档位 $1$ 开始存的是 $1$ 号剧情点；档位 $2$ 存的是 $3$ 号剧情点；档位 $1$ 后来又存了 $9$ 号剧情点。

解题思路：

无论是剧情点还是操作，处处透露着“我给出索引，你返回元素”的气息

那么我们当然是愉快的采用数据直接模拟了

但是由于存储剧情的时候直接开$10^5\ast 10^6$的二维数组毫无疑问会崩，而数据规模又给出了总数量不会超过$10^6$

于是我们采用vector动态数组存储

AC代码如下

#include 
#include 
using namespace std;
const int max_save = 100;
const int max_n = 1e5;
const int max_m = 1e5;
const int max_k = 1e6;

int save[max_save + 1];
vector<vector<int>>plots;

int main() {
	int n, m, k, to;
	cin >> n >> m;
	vector<int>init;
	plots.push_back(init);//初始化
	for (int i = 1; i <= n; i++) {
		cin >> k;
		vector<int>plot;
		plot.push_back(0);//初始化
		for (int j = 1; j <= k; j++) {
			cin >> to;
			plot.push_back(to);
		}
		plots.push_back(plot);
	}

	int choice, num, cur = 1;
	for (int i = 0; i < m; i++) {
		cin >> choice >> num;
		switch (choice) {
		case 0://前往剧情点
			cur = plots[cur][num];
			break;
		case 1://存档
			save[num] = cur;
			cout << cur << endl;
			break;
		case 2://读档
			cur = save[num];
			break;
		default:
			break;
		}
	}
	cout << cur << endl;
	return 0;
}