强化学习之入门笔记(一)
文章目录
- 强化学习
-
- 一、入门强化学习
-
- 基本元素
- 主要元素
- 核心元素
- 二、基础概念
-
- 1、马尔科夫链
- 2、马尔科夫“链”
- 3、强化学习中的Q值和V值
-
- 更复杂的未来
- Q和V的意义
- V值的定义
- Q值的定义
- V值和Q值关系
- 从Q到V
- 从V到Q
- 4、使用蒙地卡罗方法(Monte-Carlo)估算V值
-
- 先看故事
- 蒙地卡罗算法
-
- 原理
- 再进一步
- 蒙地卡罗MC的更新公式
-
- 平均香蕉
- 更进一步
- 蒙地卡罗的缺陷
- 5、使用时序差分TD估算状态V值
-
- 蒙地卡罗的限制
- 时序差分算法
- 时序差分(TD)和蒙地卡罗(MC)的比较
- 时序差分(TD)原理的直观理解
- 更新公式
- 参考
强化学习
一、入门强化学习
强化学习:智能体在与环境的互动中为了达成目标而进行的学习过程
举个超级玛丽游戏的例子,我们需要让智能体Agent,通过和环境Environment的互动中,进行学习,从而通关
这里提到了强化学习中非常基础的三个元素Agent,Environment和Goal
基本元素
1、Agent:这里智能体就是玛丽这个人物(或者是我们玩家),可以操作玛丽进行移动或者射击等行为Action
2、Environment:环境就是游戏引擎,这个环境中包括了各种要素,比如敌人,金币,台阶,砖块,花朵蘑菇等等,这个环境会实时改变,而这种改变是学习之前智能体不能完全预见的,这个环境的每一时刻,都可以用一个状态变量State来描述
3、Goal:目标就是玩家的目标,这里可以是用最快的速度通关,也可以是花费最少的生命代价通关,也可以是获得最多的金币通关。需要注意的是,这里的目标是最终的目标,而不是每一个时刻的目标,每一个时刻的目标可以称为Reward或者Return,和Goal完全不同,是两个概念,需要着重区分。当然Goal,即最终目标,也可以换算成每一个时刻的Reward做累积,但无论如何,这里的Goal是一个全过程、全局的量
我们在介绍以上三个基本元素时,又提到了以下三个主要的元素State,Action,Reward
主要元素
1、State: 状态。State是描述环境在某个时刻的变量,不同时刻的环境状态可能不同,请思考:下一个时刻的状态和什么有关?答案是:下一个时刻的状态和上一个时刻的状态有关,同时和上一个时刻的智能体动作Action有关。由于每一个时刻状态都是一个符合某种分布的随机变量,那么t 时刻的状态可以记作 S_t
2、Action:行动。Action是描述智能体和环境互动的要素。Action可以是有限种且离散的,比如超级玛丽中玩家的操作方式,上、下、左、右、大跳、小跳、射击一共七种。当然Action也可以是无限种且连续的,比如某些游戏中智能体的步幅、力度等。那么 t 时刻的智能体的行动实际上是一个符合某种分布的随机变量,可以记作 A_t
3、Reward: 奖励。奖励是智能体或者玩家当前时刻衡量对未来最终Goal的贡献,通俗来说,有点类似“小目标”。具体举例来说,玛丽拾取金币,Reward=1,玛丽通关,Reward=10000000,当然这种情况大概率发生在以通关为最终目标的学习过程中,需要注意的是,Reward是玩家根据行动后下一个时刻的状态来定义的,因此也可以说Reward是由状态State决定的。再举一个例子,围棋游戏中,某时刻智能体吃掉系统对手的棋子时,Reward可以为0,也可以为负,这是因为就整体战略上来说一时吃对面的子,未必导致最终会占领最大的地盘,存在弃小争大的可能,也就是说,在和环境的互动中,贪心策略往往不是最合理的,而reward往往可能具有延迟的性质。
将以上描述总结成一个过程,就是某时刻t ,Agent观察到Environment的状态 s_t ,从而采取行动Actiona_t ,而Environment针对Agent的行动,会更新状态为 s_{t+1},Agent获得奖励 r_t。这里之所以用小写字母是因为其并非随机变量,而是确定的观测值或者采样值了。这一过程用下图可以说明。
我们在描述智能体和环境的互动过程中时,又涉及了两个核心的问题:玩家如何行动?玩家如何评估当前状态的奖励?接下来需要介绍以下两个强化学习中核心的元素。
核心元素
1、**Policy:策略。**Policy可以被认为是一个函数,输入是状态 s 和行动a,输出是该行动在该状态下的实施概率。一般将该策略函数记作π。
π ( s , a ) → [ 0 , 1 ] π ( a ∣ s ) = P ( A = a ∣ S = s ) π(s,a)\rightarrow [0,1]\\ π(a|s)=P(A=a|S=s) π(s,a)→[0,1]π(a∣s)=P(A=a∣S=s)
举例来说,还是拿超级玛丽游戏为例,当前状态是游戏画面,该策略函数可以根据该画面计算不同的玩家行动的实施采样概率,比如左:0.2,上:0.7,右:0.1,即该场景下玩家采取的行动有20%可能是向左,有70%的可能是向上,有10%的可能是向右,如下图所示。
从原则上来说,对于固定的状态State,玩家采取的行动Action不应该是确定的,而应该是一个随机变量,玩家学习的应该是这个随机变量的更合理的一个分布。
所以,整个过程应该是,玩家观测到环境的状态 s_1,从而根据策略函数 π 采样一个行动 a_1 ,环境会更新状态为 s_2 ,此时玩家获得奖励 r_1,然后玩家根据观测到的环境状态 s_2,继续根据策略函数π 采样下一个行动 a_2,…依此进行,直到环境告诉玩家终止。如下图所示。
那么如何判断一个策略的好坏呢,我们就需要引出下一个核心元素,价值。
**2. Value:价值。**Value是衡量当前时刻直到结束时所有累计Reward的总和,由于Reward是依赖于State和Action的,所以Reward也是随机变量,而Value是累计的Reward,所以我们用记号 U 表示。
U t = R t + R t + 1 + R t + 2 + . . . + R n U_t=R_t+R_{t+1}+R_{t+2}+...+R_{n} Ut=Rt+Rt+1+Rt+2+...+Rn
但这没有考虑Reward的时间价值,明显现在的奖励比未来的奖励更重要,因此更合理的定义是:
U t = R t + γ R t + 1 + γ 2 R t + 2 + . . . + γ n − t R n γ :折旧率 U_t=R_t+\gamma R_{t+1}+{\gamma}^2 R_{t+2}+...+{\gamma}^{n-t} R_{n}\\ \gamma:折旧率 Ut=Rt+γRt+1+γ2Rt+2+...+γn−tRnγ:折旧率
因此价值越大,意味着未来获得的奖励累计总和会越多,玩家会更倾向于这种结果。
因此我们可以提出下一个很关键的函数:Value Function 价值函数。
当前的价值**依赖于当前直到未来结束所有的奖励,这些奖励又分别依赖于当前到未来结束的状态和行动**。
价值由当前直到未来结束所有的环境状态和玩家行动来决定
除了当前的状态和行动,未来的状态和行动也都是随机变量,实际上其分布也由当前的状态和行动决定,因此我们可以简单计算价值的期望!
即 E(U_t) 可以用 S_t 和 A_t来表示!这种关系就是行动价值函数 Action-Value Function!我们用 Q_{π} 表示:
Q π ( s t , a t ) = E ( U t ∣ S t = s t , A t = a t ) Q_{π}(s_t,a_t)=E(U_t|S_t=s_t,A_t=a_t) Qπ(st,at)=E(Ut∣St=st,At=at)
进一步的,我们固定状态,对所有行动求期望和,会得到状态价值函数 State-Value Function!我们用V_{π} 表示:
V π ( s t ) = E [ Q π ( s t , A ) ] V_{π}(s_t)=E[Q_{π}(s_t,A)] Vπ(st)=E[Qπ(st,A)]
总结来说,给定一个策略函数 π ,行动价值函数 Q_{π}(s,a) 可以衡量智能体在状态 s 下实施行动 a的好坏。而状态价值函数V_{π}(s) 可以衡量智能体在状态 s 的当下形势好坏。因此,衡量一个策略函数的好坏可以用以下指标:
E S [ V π ( S ) ] E_S[V_{π}(S)] ES[Vπ(S)]
提示一下,智能体既可以学习策略函数 π 直接来和环境互动学习,也可以 学习行动价值函数 Q_{π},选择使得价值最大的路径来和环境互动学习,这就是两种不同的强化学习方法了,分别叫做Policy-Based 和Value-Based方法。
上面的是不是没有看懂,没关系,我当时也没有搞懂,请继续往下看
二、基础概念
1、马尔科夫链
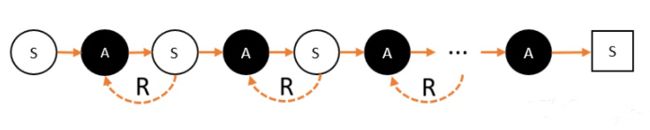
我们先来看马尔科夫链。马尔科夫链长这样子:
马可洛夫链描述的是智能体和环境进行互动的过程。简单说:智能体在一个状态(用S代表)下,选择了某个动作(用A代表),进入了另外一个状态,并获得奖励(用R代表)的过程
S(state)状态,在图中用白色圈圈表示
状态就是智能体观察到的当前环境的部分或者全部特征
举个例子:无人驾驶汽车来到十字路口。和人类一样,它需要先“观察”这个路口的情况,再决定一下步的"动作"
无人驾驶汽车通过摄像头,可以观察到交通标志、交通信号灯等情况;通过雷达,可以探测到与其他汽车、行人的距离;通过导航系统,了解前方的路段是否通畅等等。这些被观察到的环境特征,就是无人驾驶汽车的状态特征, 状态空间就是智能体能够观察到的特征数量
需要特别注意的是:环境的特征可能有许多,但只有智能体能够观察到的特征才算是状态,所以我们也用Observation表示状态
强调被观察的原因:
- 提醒我们要给智能体最有用的特征。因为在实际工作中,输入特征往往是很“贵”的,无人驾驶汽车的摄像头,雷达通常都是很昂贵的。而无用的特征,例如是否有乘客在唱歌之类的,输入到自动驾驶系统,这无疑加重了学习的负担。所以,我们必须非常慎重地选择状态特征。
- 提醒我们要注意观察的角度。假设我们学有所成,希望做一个智能体学习如何打德州扑克。你就会突然发现,这个状态很微妙。因为对于每位玩家,都只看到自己的牌和公关牌,所以观察到的状态都是不一样的。
A(action)动作(用黑色圈圈表示)
动作其实不用解释,就是智能体做出的具体行为。例如扫地机器人会移动,吸尘,甚至喷水。无人驾驶汽车能够移动,加速,刹车,转弯等
动作空间就是该智能体能够做出的动作数量
举个例子:智能体身处十字路口。那么我们的方向就有4个。也就是说,我们能做的动作,就是4个。我们称我们能做的动作的集合,称为动作空间
R(reward)奖励
当我们在某个状态下,完成动作。环境就会给我们反馈,告诉我们这个动作的效果如何。这种效果的数值表达,就是奖励。
其实这里的reward翻译为“反馈”可能更合适一点。因为反馈并不是完全正面的,也有负面。
当reward是正数时,表示鼓励当前的行为;如果reward是负数,表示惩罚这种行为;当然,reward也可以是0。
奖励在强化学习中,起到了很关键的作用,我们会以奖励作为引导,让智能体学习做能获得最多奖励的动作
例如:我需要训练机器人打乒乓球。机器人每次赢球,都可以加分;输球,就减分。这分数就表现了机器人的动作好坏。如果机器人希望获得更多的分数,就需要想办法赢球。
又例如:无人驾驶汽车如果成功到达目标地点,那么可以获得奖励;但如果闯红灯,那么就会被扣除大量的奖励作为惩罚。如果无人驾驶汽车希望获得更多的分数,那么就必须在遵守交通规则的情况下,成功到达目标地点。
奖励的设定是主观的,也就是说我们为了智能体更好地学习工作,自己定的
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rZTf6j4b-1679663118417)(pic/04马克洛夫链.png)]
- 智能体在环境中,观察到状态(S);
- 状态(S)被输入到智能体,智能体经过计算,选择动作(A);
- 动作(A)使智能体进入另外一个状态(S),并返回奖励(R)给智能体;
- 智能体根据返回,调整自己的策略;重复以上步骤,一步一步地创造马尔科夫链
强化学习跟教孩子是一个道理: 孩子做了好事,必须给奖励;孩子做错事了,必须惩罚
2、马尔科夫“链”
所以,我们马上遇到第一个坑:马尔科夫链,其实应该叫马尔科夫树
马尔科夫链之所以是我们现在看到的一条链条,是因为我们站在现在,往后看,所以是一条确定的路径;但如果我们往前看,就并不是一条路径,而是充满了各种“不确定性”
这就像我们从家里到公司上班,中间有若干种上班的方式。现在你从家里出门,走过了两个路口,到了公交车站。 这时候往后看,从家到公交车站这一路,只能有一条路径。虽然你可以走其他路到公交车站,但这是你走过的路,已经确定下来了,所以路径只有一条;但如果往前看,从公交车坐车到公司,还有很多种方式到达,向前展开的是各种不确定性
理解这一点很重要,这是理解强化学习理论的基础。为了更好理解,我们举个例子:
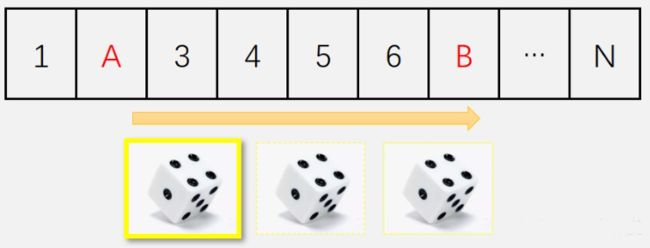
假设现在我们来玩这样一个游戏。这个游戏是简化版的大富翁,我们只考虑我们当前所处位置,也就是状态。智能体移动的时候,它可以选择投掷1-3个骰子,根据骰子点数的总和向前移动:
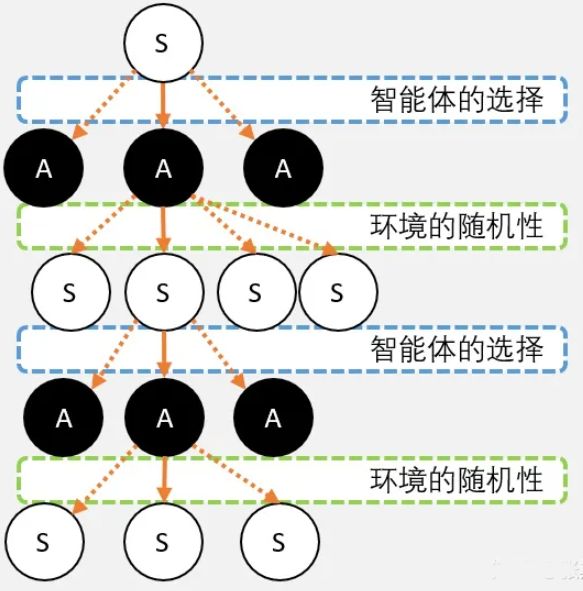
现在,智能体从格子A掷骰子,并移动到格子B。其实经历了两次不确定性:
- 第一次,是“选择”的过程。智能体主动选择骰子的个数。掷骰子的个数不同,到达格子B的概率也不同。所以“选择”会影响到下一个状态。这种不同动作之间的选择,我们称为智能体的策略。策略我们一般用Pi表示。我们的任务就是找到一个策略,能够获得最多的奖励。
- 第二次的不确定性,是环境的随机性,这是智能体无法控制的。在这个例子里就是骰子的随机性。注意,并不是所有环境都有随机性,有些环境是很确定的(例如把以上所有骰子每一面都涂成1点),但马尔科夫链允许我们有不确定性的存在。
从上面的例子我们知道,这种不确定性来自两个方面:智能体的行动选择(策略);环境的不确定性。
就比如在路口,闯红灯和等绿灯是我的选择,但是不同选择后面的环境随机性给出的概率是不一样的。虽然我们不能控制环境的随机性,但我们能够控制我们的选择,让我们避免高风险低回报的情况出现
马尔科夫链是用来描述智能体和环境互动的过程
马尔科夫链包含三要素:state、action、reward
- state:只有智能体能够观察到的才是state
- action:智能体的动作
- reward:引导智能体工作学习的主观的值
强化学习的核心思想:如果你不希望孩子有某种行为,那么当这种行为出现的时候就进行惩罚。如果你希望孩子坚持某种行为,那么就进行奖励
3、强化学习中的Q值和V值
马尔科夫告诉我们:当智能体从一个状态S,选择动作A,会进入另外一个状态S‘;同时,也会给智能体奖励R。奖励既有正,也有负。正代表我们鼓励智能体在这个状态下继续这么做;负代表我们并不希望智能体这么做
但更多的时候,我们并不能单纯通过R来衡量一个动作的好坏。来看下面一个例子:
假设,10天之后进行期末考试,我们今天有两个选择: 1. 放弃吧,我们玩游戏!我们每天可以获得+1心情值; 2. 决心努力一搏,我们开始学习吧!每天我们-2心情值。
从这10天看,我们肯定是选择【1.玩游戏】。因为10天后,我们虽然考试没过,但至少收获10天的快乐。
但事实上,我们再看远一点:
- 因为挂科,接受老师怒吼攻击!心情值马上减5;
- 父母因为我考得好成绩,给了更多的零用钱。心情值加200点。
所以,假设我们能预知未来,我们一定会选择【2.去复习】
因此,我们必须用长远的眼光来看待问题,我们要把未来的奖励也计算到当前的状态下,再进行决策
更复杂的未来
但在实际情况中,比我们刚才想想要复杂得多。
我们之前说过,未来是充满不确定性的,不确定性既包含在我们的策略,也包含在环境之中。
也就是说,即使我现在努力学习,我也不能100%保证我我一定考得好成绩。即使有好成绩,父母也不一定会给我更多零用钱。但即使挂科了,老师也不一定大发雷霆。
嗯,好吧。那看上去还是应该及时行乐,选择打游戏!
嗯,学渣永远是学渣(就比如本人),而你的学霸朋友(如果有的话),会先让你算一下:
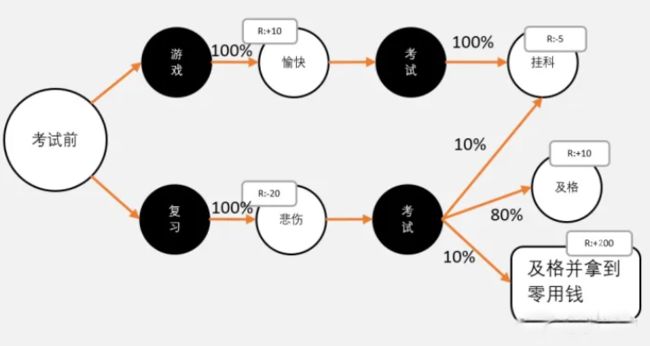
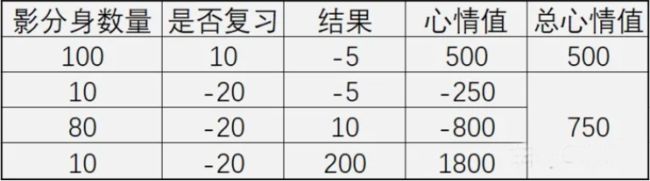
我们把当前状况再理一下: 1. 10天后考试,玩游戏1天,心情+1;复习1天,心情-2。10天后,玩游戏心情+10,复习心情-20。 2. 不复习,100%挂科,被老师怒吼:-5点心情 3. 复习,10%挂科,同样被老师怒吼:-5点心情;80%不挂科,努力终于有回报:+10点心情;10%不挂科,且得到父母的零用钱 心情暴击+200点。
学霸深情地对学渣说:我知道你对概率和期望不太熟悉,那么我们现在就用影分身大法吧
假设,有100个你自己,所有你都在玩游戏,并且所有的你都挂科了。 如果选择不复习。那么100个你一共可以获得多少奖励?
学渣:这我会! - 10天都在玩,那么玩游戏心情就+10,100个我就是1000点心情! - 必定会挂科了-5,100个分身就是-500点。所以最终+500点心情,那么就加500点心情!果然还是打游戏比较划算。
学霸: 你别兴奋呀,那如果复习呢? 学渣: - 10个分身挂科,这些分身复习了,-20心情;复习了还挂科,-5心情;一共-250心情值。 - 80个分身不挂科,这些分身复习了,-20心情;但不挂科,+10,最终还是只有-10点心情,80个我最终-800。 - 还有10个分身不挂科,而且获得父母的零用钱,因为复习-20心情,最终+1800点。
哇!比去玩的还多!我必须马上学习!
看完上面的故事,学霸可能会觉得麻烦。那不就是概率求期望么,真的要这么麻烦吗?
但在实际运用中,大多时候我们并不知道真实概率是多少。以上的概率都是我们自己估算,没有经过验证的。
在强化学习中,我们为了获得概率,我们将会不断地让我们智能体重复,或者让多个智能体进行试验以获得数据。
Q和V的意义
所以我们在做决策的时候,需要把眼光放远点,把未来的价值换到当前,才能做出选择
为了方便,我们希望我们可以有一种方法衡量我们做出每种选择价值。这样,我们只需要看一下标记,以后的事情我也不用理了,我们选择哪个动作价值更大,就选那个动作就可以了
也就是说,我们让复习和游戏都有一个标记,这个标记描述了这个动作的价值:- 游戏 +500 - 复习 +750
当然,我们也可以把这个标记标在状态上
评估动作的价值,我们称为Q值:它代表了智能体选择这个动作后,一直到最终状态奖励总和的期望
评估状态的价值,我们称为V值:它代表了智能体在这个状态下,一直到最终状态的奖励总和的期望
价值越高,表示从当前状态到最终状态能获得的平均奖励将会越高
应为智能体的目标是获取尽可能多的奖励,所以智能体在当前状态,只需要选择价值高的动作就可以了
V值的定义
上面的定义理解起来好难,我们用“影分身”大法,理解起来就容易多了
假设现在需要求某状态S的V值,那么我们可以这样:
- 我们从S点出发,并影分身出若干个自己;
- 每个分身按照当前的策略 选择行为;
- 每个分身一直走到最终状态,并计算一路上获得的所有奖励总和;
- 我们计算每个影分身获得的平均值,这个平均值就是我们要求的V值。
用大白话总结就是:从某个状态,按照策略 ,走到最终状态很多很多次;最终获得奖励总和的平均值,就是V值
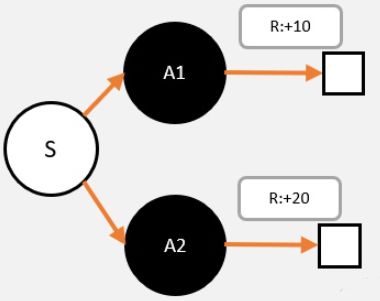
【敲黑板】 1. 从V值的计算,我们可以知道,V值代表了这个状态的今后能获得奖励的期望。 2. V值跟我们选择的策略有很大的关系。 我们看这样一个简化的例子,从S出发,只有两种选择,A1,A2;从A1,A2只有一条路径到最终状态,获得总奖励分别为10和20
现在我们假设策略 采用平均策略[A1:50%,A2:50%],直接求期望,那么我们可以求得V值为15
现在我们改变策略[A1:60%,A2:40%],那么我们可以求得V值为14,变少了
所以大家看到,V值是会根据不同的策略有所变化的
Q值的定义
Q值和V值的概念是一致的,都是衡量在马尔科夫树上某一个节点的价值。只不过V值衡量的是状态节点的价值,而Q值衡量的是动作节点的价值
和V值一样,我们也可以用影分身来理解Q值。
现在我们需要计算,某个状态S0下的一个动作A的Q值: 1. 我们就可以从A这个节点出发,使用影分身之术; 2. 每个影分身走到最终状态,并记录所获得的奖励; 3. 求取所有影分身获得奖励的平均值,这个平均值就是我们需要求的Q值
用大白话总结就是:从某个状态选取动作A,走到最终状态很多很多次;最终获得奖励总和的平均值,就是Q值
【敲黑板】 与V值不同,Q值和策略并没有直接相关,而与环境的状态转移概率相关,而环境的状态转移概率是不变的
V值和Q值关系
V值和Q值都是马尔科夫树上的节点
V值和Q值的评价方式是一样的: - 从当前节点出发 - 一直走到最终节点 - 所有的奖励的期望值
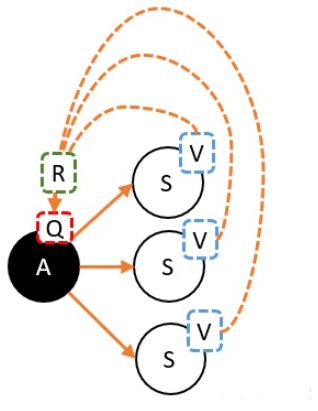
从Q到V
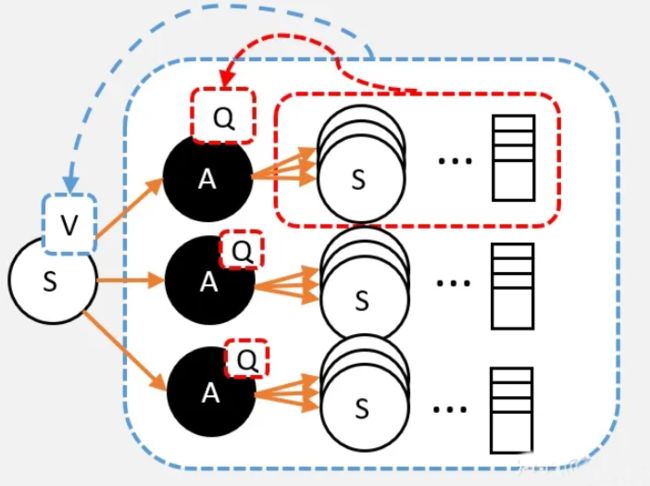
从定义出发,我们要求的V值,就是从状态S出发,到最终获取的所获得的奖励总和的期望值。也就是蓝色框部分
S状态下有若干个动作,每个动作的Q值,就是从这个动作之后所获得的奖励总和的期望值。也就是红色框部分
假设我们已经计算出每个动作的Q值,那么在计算V值的时候就不需要一直走到最终状态了,只需要走到动作节点,看一下每个动作节点的Q值,根据策略 ,计算Q的期望就是V值了
更正式的公式如下:
v π ( s ) = ∑ a ∈ A π ( a ∣ s ) q π ( s , a ) v π ( s ) : V 值 π ( a ∣ s ) :策略 q π ( s , a ) : Q 值 v_{\pi}(s)=\sum_{a \in A}\pi (a|s)q_{\pi}(s,a)\\ v_{\pi}(s):V值\\ \pi (a|s):策略\\ q_{\pi}(s,a):Q值 vπ(s)=a∈A∑π(a∣s)qπ(s,a)vπ(s):V值π(a∣s):策略qπ(s,a):Q值
大白话就是:一个状态的V值,就是这个状态下的所有动作的Q值,在策略 下的期望
从V到Q
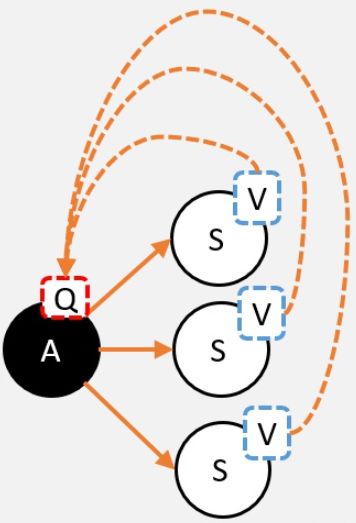
道理还是一样,就是用Q就是V的期望!而且这里不需要关注策略,这里是环境的状态转移概率决定的
对,但还差点东西
当我们选择A,并转移到新的状态时,就能获得奖励,我们必须把这个奖励也算上!
更正式的公式如下:
q π ( s , a ) = R s a + γ ∑ s ′ P s s ′ a v π ( s ′ ) q π ( s , a ) : Q 值 R s a :奖励 γ :折扣率 P s s ′ a :状态转移率 v π ( s ′ ) : V 值 q_{\pi}(s,a)=R_{s}^{a}+\gamma \sum_{s'}P_{ss'}^{a}v_{\pi}(s')\\ q_{\pi}(s,a):Q值\\ R_{s}^{a}:奖励\\ \gamma:折扣率\\ P_{ss'}^{a}:状态转移率\\ v_{\pi}(s'):V值\\ qπ(s,a)=Rsa+γs′∑Pss′avπ(s′)qπ(s,a):Q值Rsa:奖励γ:折扣率Pss′a:状态转移率vπ(s′):V值
折扣率 在强化学习中,有某些参数是人为主观制定。这些参数并不能推导,但在实际应用中却能解决问题,所以我们称这些参数为超参数,而折扣率就是一个超参数。我们计算Q值,目的就是把未来很多步奖励,折算到当前节点。但未来n步的奖励的10点奖励,与当前的10点奖励是否完全等价呢?未必。所以我们人为地给未来的奖励一定的折扣,例如:0.9,0.8,然后在计算到当前的Q值。
现在我们知道如何从V到Q,从Q到V了。但实际应用中,我们更多会从V到V。
但其实从V到V也是很简单的。把公式代进去就可以了。
v π ( s ) = ∑ a ∈ A π ( a ∣ s ) ( R s a + γ ∑ s ′ ∈ S P s s ′ a v π ( s ′ ) ) v_{\pi}(s)=\sum_{a \in A}\pi(a|s)(R_{s}^a+\gamma\sum_{s' \in S}P_{ss'}^a v_{\pi}(s')) vπ(s)=a∈A∑π(a∣s)(Rsa+γs′∈S∑Pss′avπ(s′))
- 比起记住公式,其实我们更应该注意Q值和V值的意义:就是假设从这个节点开始,走许多许多次,最终获取的奖励的期望
- V就是子节点的Q的期望!但要注意V值和策略相关
- Q就是子节点的V的期望!但要注意,记得把R计算在内
大家有没有发现,在这一节中,计算某一个节点的Q值和V值,需要许多次试验,取其中的平均值。但实际上,我们不但需要求一个节点的值,而是求所有节点的值。如果我们每一个节点都用同样的方法,消耗必然会很大。所以人们发明了许多方式去计算Q值和V值,基于价值计算的算法就是围绕Q和V展开的
4、使用蒙地卡罗方法(Monte-Carlo)估算V值
蒙地卡罗是著名的赌城,少数机智赌徒为了赢钱,活生生被逼成了数学家,因此在这里出现了很多有关概率的理论
先看故事
话说,齐天大圣孙悟空,护送唐三藏到西方取经。路过一神秘洞穴,突然被怪物的法宝葫芦吸了进去。
葫芦里面原来是另外一个次元的世界,大圣转了两圈,怎么都出不去。气的大圣破口大骂,可是又破坏不了这葫芦。正在踌躇之际,前面来了一个人。
说道:大圣呀,我是来自西域的蒙地卡罗,我被困在这里很久啦。
这个迷宫呀,不但要我们找到出口,而且要我们找出从任何一个位置离出口最近的路呀。
但大圣请放心,只要大圣助我一臂之力,我定可以解决这个问题。
大圣,你如此如此,这般这般便可。
大圣听道,连忙点头称是。
于是大圣从身上拔下一条汗毛,轻轻一吹,变成了小猴。于是大圣开始吩咐小猴:
1、你从这里出去之后,就随便逛,走的时候要记住走的路径 和 每一步获得的奖励。 2、如果你到了最终出口,那就沿原路往回走,在每个经过的路口,留下一张字条: 字条上写上你获得的奖励 加上 你上一个路口的标记的路口的价值。这个价值你可以乘以一个折扣,嗯,就乘以0.9吧。 3、你就这样一直沿路回来可以了。
于是小猴一蹦一跳就出去了,过了一会,回来了。
这时候大圣正在吃香蕉,看到小猴回来,扔了一根香蕉给小猴,说: 你继续出去吧,和上次一样就好啦。
小猴不解道:那如果遇到我上次见到的路口,我是应该怎么做呢?
大圣想了一下说:你不用管,你把这一次的数给记下就可以了。大圣又给了小猴一根香蕉。让小猴继续跑。
小猴就是这样,一直跑一直跑,跑了许多次,蒙地卡罗的赌徒跟大圣说:大圣爷,我看差不多了,你去让小猴子,把所有的数都给平均一下,就是我们要求的V值了。
蒙地卡罗算法
看完上面的故事,应该对蒙地卡罗算法有大概的认识。现在我们来具体看看蒙地卡罗算法。
- 我们把智能体放到环境的任意状态;
- 从这个状态开始按照策略进行选择动作,并进入新的状态;
- 重复步骤2,直到最终状态;
- 我们从最终状态开始向前回溯:计算每个状态的G值;
- 重复1-4多次,然后平均每个状态的G值,这就是我们需要求的V值。
原理
其实从直觉上,我们很容易理解。
我们分成两部分,首先我们要理解每一次我们算的G值的意义。
- 第一步,我们根据策略往前走,一直走到最后,期间我们什么都不用算,还需要记录每一个状态转移,我们获得多少奖励r即可
- 第二步,我们从终点往前走,一遍走一遍计算G值。G值等于上一个状态的G值(记作G’),乘以一定的折扣(gamma),再加上r
所以G值的意义在于,在这一次游戏中,某个状态到最终状态的奖励总和(理解时可以忽略折扣值)
当我们进行多次试验后,我们有可能会经过某个状态多次,通过回溯,也会有多个G值。 重复我们刚才说的,每一个G值,就是每次到最终状态获得的奖励总和。而V值时候某个状态下,我们通过影分身到达最终状态,所有影分身获得的奖励的平均值。
所以大家看到,其实当我们之前理解清楚V值和Q值的意义,我们理解蒙地卡罗其实很轻松的
再进一步
- G的意义:在某个路径上,状态S到最终状态的总收获
- V和G的关系:V是G的期望
到这里要注意一点:V和策略是相关的,那么在这里怎么体现呢?
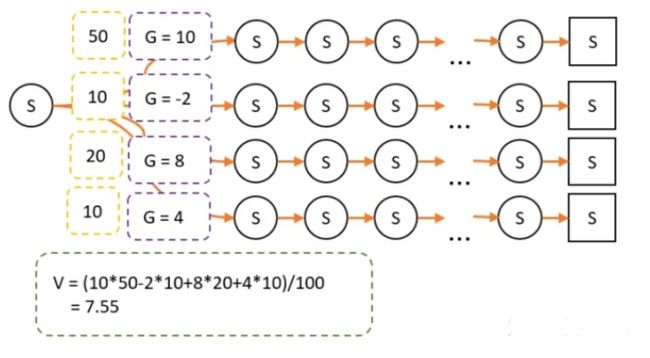
我们仍以上图为例子,以策略A进行游戏。其中有100次经过S点,经过S点后有4条路径到达最终状态,计算G值和每条路径次数分别如下:
策略A采用平均策略,这时候 V = 5
现在我们采用策略B,由于策略改变,经过某条路径的概率就会产生变化。因此最终试验经过的次数就不一样了
最终计算的 V = 7.55
蒙地卡罗MC的更新公式
蒙地卡罗的V,其实就是多次G的平均值
样计算其实相当麻烦,因为每一个状态都需要建立一个空间,记录每个轨迹下的G值。
那有没有一种方法,可以用更少的空间计算V值呢?当然有
平均香蕉
有两条长度分别为A,B的香蕉(并假设:A>B)。 如果我要知道他们平均有多长。我只需要把A切成和B长;然后把多出来的那一节,再切一半,接到B就可以了。这时候,我们称那条加长了的B香蕉为平均香蕉。
如果这时候有第三条C呢?其实原理也一样,比较一下C和平均香蕉,然后把差切出来。但这个时候因为我们有3条香蕉要平均,所以我们要分3份,再接到平均香蕉上。再来一根香蕉也一样。
V是G的平均值,但我们可以用增量更新的方式: 现在我们只需要记录之前的平均值V,新加进来的G,和次数N。我们把V和G的差,除以N,然后再加到原来的平均值V上,就能计算到新的V值。
V n e w = ( V o l d − G ) ∗ ( 1 / N ) + V o l d V o l d :原来的 V 值,也就是平均香蕉 G :这一次回溯后,计算出来的 G 值,也就是新加进来的香蕉 N : 这个状态被经过多少次了 V n e w :新计算出来的 V 值,也就是平均香蕉 V_{new} = (V_{old} - G) * (1 / N) + V_{old}\\ V_{old}:原来的V值,也就是平均香蕉\\ G:这一次回溯后,计算出来的G值,也就是新加进来的香蕉\\ N: 这个状态被经过多少次了\\ V_{new}:新计算出来的V值,也就是平均香蕉 Vnew=(Vold−G)∗(1/N)+VoldVold:原来的V值,也就是平均香蕉G:这一次回溯后,计算出来的G值,也就是新加进来的香蕉N:这个状态被经过多少次了Vnew:新计算出来的V值,也就是平均香蕉
更进一步
但其实这样计算还是比较麻烦,我们甚至可以不用记录N,把(1/N)设置成为一个固定的数,例如0.1、0.2(还记得超参数吗?)。我们把这个值称为学习率
这就相当于,我们新来的香蕉G和平均香蕉V的差的十分之一,会被加到平均香蕉上!也就是说,每一次G都会引导V增加一些或者减少一些,而这个V值慢慢就会接近真正的V值。
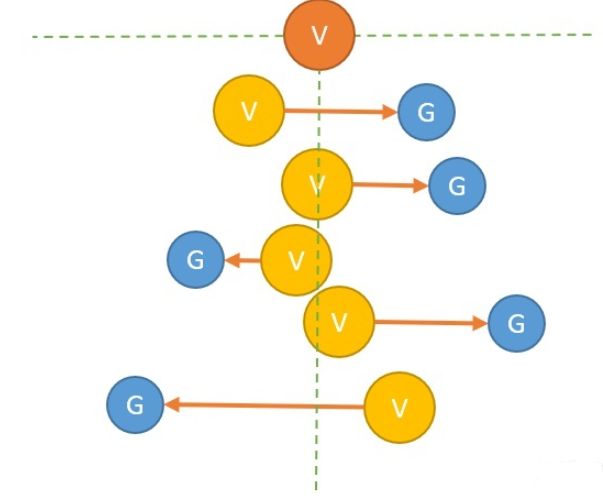
但这数值不就是不对了吗?但为什么可以这样做呢? 这是因为V值是一个"客观存在"的值,我们可以用任何其他方式去求它。而G值是围绕V值的值,G每次出现会都往自己身边拉一下。 就像很多个G在拔河,有的G比V大,有的比G小,有的G力气大,有的G力气小。但没问题,当有足够多的G在的时候,他们一起拉,V就会接近于那个客观存在的V值。
图中:我们假设橙色的V是客观存在的那个V值,G值会一次又一次把现在的V值(黄色)往左右拉,当次数足够多的时候。V值就和真实的V值很接近了。
所以,我们把这里的G,也称为V的更新目标
而学习率就可以理解为,每次V向目标靠近的幅度;学习率越大,表示向G靠近的幅度越大,反之则越小。但是不是越大越好呢?
因此,我们可以用两种角度理解MC的更新公式:
第一种,我们用“平均香蕉”来理解
第二种,我们用“G的拔河”来理解
蒙地卡罗的缺陷
但蒙地卡罗有一个比较大的缺点,就是每一次游戏,都需要先从头走到尾,再进行回溯更新。如果最终状态很难达到,那小猴子可能每一次都要转很久很久才能更新一次G值。
而使用时序差分(TD)算法可以解决蒙地卡罗算法的缺陷
5、使用时序差分TD估算状态V值
蒙地卡罗的限制
虽然蒙地卡罗算法能够在不知道环境信息的时候,以采样的方式估算V值。但这种方法也是有一定的限制:
- 蒙地卡罗算法相对动态规划,会有点不那么准。因为蒙地卡罗每一次的路径都是不一样的
- 如果环境的状态空间非常大,或者最终状态只有非常小的概率达到。那么蒙地卡罗算法将会很难处理
时序差分算法
原文再续,书接上一回。
话说,孙大圣和来自蒙地卡罗的小蒙,一起解决了第一个问题。而让人想不到的是,还有第二关,而且这关的迷宫更大了。
没办法,大圣只能按照之前的方法去计算V值。
但这迷宫实在太大了,小猴子根本找不到出口。终于,疲惫后的猴子实在太累了。走到一半,就回头更新了。
然而,这怎么瞒得过孙大圣的火眼金睛,大圣正想发怒。小蒙却阻止道:等等,让我想想。
几分钟后,小蒙惊喜道:大圣爷,想不到呀,这小猴乱打乱撞,却让我发现了新的算法。
大圣狐疑道:真的?!
小蒙:真的,我们姑且把这个算法叫做时序差分算法吧。
大圣:那你说来听听,如果没道理,哼,吃老孙一棒。
小蒙:是的是的
于是小蒙便把这个时序差分算法说出来,为了方便,以后我们就叫TD算法: 1. 小猴子每走1步,看一下这个路口的V值,还有获得的奖励r; 2. 回到原来的路口,把刚刚看到的V值和奖励r进行运算,估算出V值
于是小猴子便用这种方式,很快地计算出各个路口的V值
时序差分(TD)和蒙地卡罗(MC)的比较
TD算法对蒙地卡罗(MC)进行了改进:
- 和蒙地卡罗(MC)不同:TD算法只需要走N步,就可以开始回溯更新
- 和蒙地卡罗(MC)一样:小猴需要先走N步,每经过一个状态,把奖励记录下来,然后开始回溯
- 那么,状态的V值怎么算呢?其实和蒙地卡罗一样,我们就假设N步之后,就到达了最终状态了。
- 假设“最终状态”上我们之前没有走过,所以这个状态上的纸是空白的,这个时候我们就当这个状态为0;
- 假设“最终状态”上我们已经走过了,这个状态的V值,就是当前值。然后我们开始回溯。
时序差分(TD)原理的直观理解
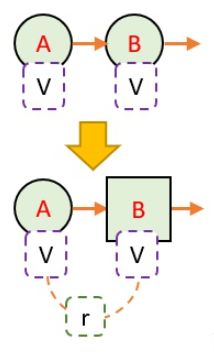
我们可以把TD看成是这样一种情况:我们从A状态,经过1步,到B状态。我们什么都不管就当B状态是最终状态了
但B状态本身就带有一定的价值,也就是V值。其意义就是从B状态到最终状态的总价值期望
我们假设B状态的V值是对的,那么,通过回溯计算,我们就能知道A状态的更新目标了
这就有点像从山顶像知道要下山的路有多长。 MC能直接走一趟,看一下到底有多远。 TD则轻巧一点,先走一段路看一下,看一下有没有路牌指示到山脚还有多远。如果有,那么就把刚刚走的那段路加上路牌指示到山脚的距离相加即可。 但又同学可能会问,在一开始,我们根本没有路牌呀,所以也不知道到底到山脚有多远。 没错,这是对的。但当我们走很多次的时候,路牌系统就能慢慢建立起来。 例如第一次,只有到了山脚,我才知道山脚前一站离山脚的的真实距离。于是我更新了山脚前一站的路牌。第二次,我在山脚前一站路就能看到路牌,所以我就可以更新山脚前一站的路牌了…一直到山顶,就这样一直建立整座山的路牌系统。
更新公式
刚刚我们对TD有个直观的理解:TD并不是走完整段路径,而是半路就截断,用半路的路牌,更新当前的路牌
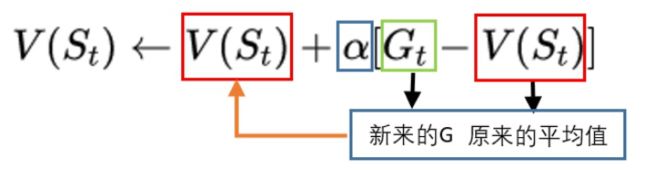
我们只需把MC的更新目标,改为TD的更新目标即可
在MC中,G是更新目标;而在TD中,我们只不过把更新目标从G,改成了R + gamma * V
王树森有一段解释TD算法的话,大意是“用更可靠的估计取代现有估计”,V(St)是现有估计,r+V(St+1)是更可靠估计,因为其中多了真实值r,所以不断用更可靠估计取代现有估计,就能慢慢接近真实值
参考
1、原创 | 一文读懂强化学习:https://mp.weixin.qq.com/s?__biz=MzI1MjQ2OTQ3Ng==&mid=2247585916&idx=1&sn=331a4424bd68f51b90590137bd6a8732&chksm=e9e099f7de9710e167ef756aef82511fe009bf03dd7862819f39cfb519ab65dca0e057f1defc&scene=27
2、怎样正确理解马尔科夫链:https://zhuanlan.zhihu.com/p/109217883
3、如何理解强化学习中的Q值和V值:https://zhuanlan.zhihu.com/p/109498587
4、如何用蒙地卡罗方法(Monte-Carlo)估算V值:
https://zhuanlan.zhihu.com/p/109755443
5、蒙地卡罗MC的更新公式怎么来的:https://zhuanlan.zhihu.com/p/110118392
6、如何用时序差分TD估算状态V值:https://zhuanlan.zhihu.com/p/110132710