时间序列预测方法总结
时间序列预测方法总结
- 数据准备
- 方法1:朴素法
- 方法2:简单平均法
- 方法3:移动平均法
- 方法4:简单指数平滑法
-
- 平面预测
- 优化
- 方法5:霍尔特(Holt)线性趋势法
- 方法6:Holt-Winters季节性预测模型
-
- 加法分量形式
- 方法7:自回归移动平均模型(ARIMA)
https://www.biaodianfu.com/python-time-series-forecasting-methods.html
数据准备
数据集(JetRail高铁的乘客数量)下载
假设要解决一个时序问题:根据过往两年的数据(2012 年 8 月至 2014 年 8月),需要用这些数据预测接下来7个月的乘客数量。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
df = pd.read_csv("train.csv")
df.head()
| ID | Datetime | Count | |
|---|---|---|---|
| 0 | 0 | 25-08-2012 00:00 | 8 |
| 1 | 1 | 25-08-2012 01:00 | 2 |
| 2 | 2 | 25-08-2012 02:00 | 6 |
| 3 | 3 | 25-08-2012 03:00 | 2 |
| 4 | 4 | 25-08-2012 04:00 | 2 |
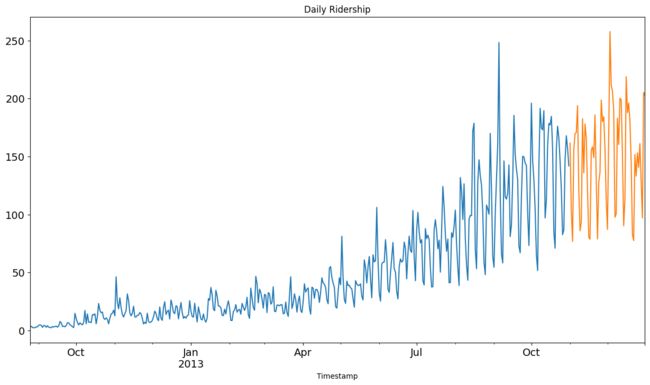
依照上面的代码,我们获得了 2012-2014 年两年每个小时的乘客数量。为了解释每种方法的不同之处,以每天为单位构造和聚合了一个数据集。
从 2012 年 8 月- 2013 年 12 月的数据中构造一个数据集。
创建 train and test 文件用于建模。前 14 个月( 2012 年 8 月- 2013 年 10 月)用作训练数据,后两个月(2013 年 11 月 – 2013 年 12 月)用作测试数据。
以每天为单位聚合数据集。
import matplotlib.pyplot as plt
import pandas as pd
# Subsetting the dataset
# Index 11856 marks the end of year 2013
df = pd.read_csv("train.csv", nrows=11856)
# Creating train and test set
# Index 10392 marks the end of October 2013
train = df[0:10392]
test = df[10392:]
# Aggregating the dataset at daily level
df["Timestamp"] = pd.to_datetime(df["Datetime"], format="%d-%m-%Y %H:%M")
df.index = df["Timestamp"]
df = df.resample("D").mean()
train["Timestamp"] = pd.to_datetime(train["Datetime"], format="%d-%m-%Y %H:%M")
train.index = train["Timestamp"]
train = train.resample("D").mean()
test["Timestamp"] = pd.to_datetime(test["Datetime"], format="%d-%m-%Y %H:%M")
test.index = test["Timestamp"]
test = test.resample("D").mean()
# Plotting data
train.Count.plot(figsize=(15, 8), title="Daily Ridership", fontsize=14)
test.Count.plot(figsize=(15, 8), title="Daily Ridership", fontsize=14)
plt.show()
C:\Users\suny\AppData\Local\Temp\ipykernel_15144\275037429.py:16: FutureWarning: The default value of numeric_only in DataFrameGroupBy.mean is deprecated. In a future version, numeric_only will default to False. Either specify numeric_only or select only columns which should be valid for the function.
df = df.resample("D").mean()
C:\Users\suny\AppData\Local\Temp\ipykernel_15144\275037429.py:20: FutureWarning: The default value of numeric_only in DataFrameGroupBy.mean is deprecated. In a future version, numeric_only will default to False. Either specify numeric_only or select only columns which should be valid for the function.
train = train.resample("D").mean()
C:\Users\suny\AppData\Local\Temp\ipykernel_15144\275037429.py:24: FutureWarning: The default value of numeric_only in DataFrameGroupBy.mean is deprecated. In a future version, numeric_only will default to False. Either specify numeric_only or select only columns which should be valid for the function.
test = test.resample("D").mean()
我们将数据可视化(训练数据和测试数据一起),从而得知在一段时间内数据是如何变化的。
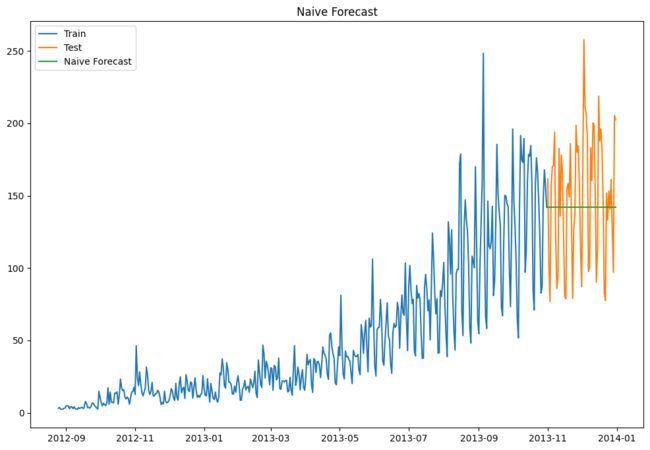
方法1:朴素法
如果数据集在一段时间内都很稳定,我们想预测第二天的价格,可以取前面一天的价格,预测第二天的值。这种假设第一个预测点和上一个观察点相等的预测方法就叫朴素法。
y ^ t + 1 = y t \hat{y}_{t+1}=y_t y^t+1=yt
dd = np.asarray(train["Count"])
y_hat = test.copy()
y_hat["naive"] = dd[len(dd) - 1]
print(y_hat)
plt.figure(figsize=(12, 8))
plt.plot(train.index, train["Count"], label="Train")
plt.plot(test.index, test["Count"], label="Test")
plt.plot(y_hat.index, y_hat["naive"], label="Naive Forecast")
plt.legend(loc="best")
plt.title("Naive Forecast")
plt.show()
ID Count naive
Timestamp
2013-11-01 10403.5 161.583333 142.0
2013-11-02 10427.5 103.083333 142.0
2013-11-03 10451.5 76.833333 142.0
2013-11-04 10475.5 156.416667 142.0
2013-11-05 10499.5 169.750000 142.0
... ... ... ...
2013-12-27 11747.5 161.166667 142.0
2013-12-28 11771.5 128.500000 142.0
2013-12-29 11795.5 97.083333 142.0
2013-12-30 11819.5 205.333333 142.0
2013-12-31 11843.5 202.500000 142.0
[61 rows x 3 columns]
朴素法并不适合变化很大的数据集,最适合稳定性很高的数据集。我们计算下均方根误差,检查模型在测试数据集上的准确率:
from math import sqrt
from sklearn.metrics import mean_squared_error
rms = sqrt(mean_squared_error(test["Count"], y_hat["naive"]))
print("最终均方根误差RMS为:", rms)
最终均方根误差RMS为: 43.91640614391676
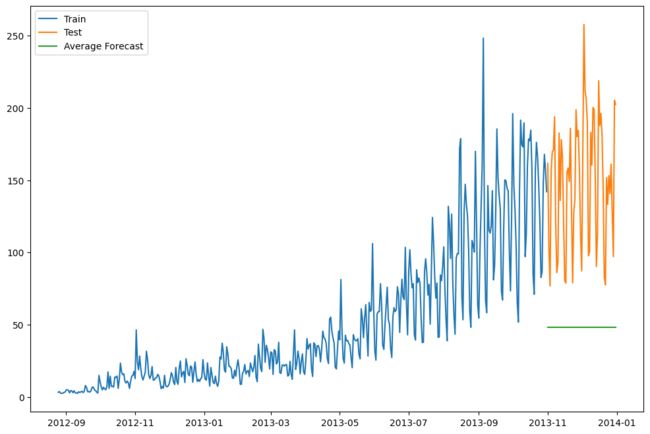
方法2:简单平均法
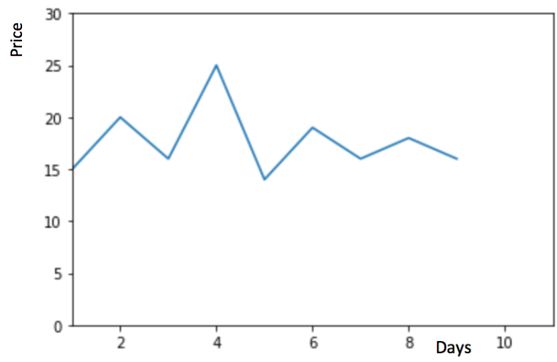
我们假设y轴表示某个物品的价格,x轴表示时间(天)。
物品价格会随机上涨和下跌,平均价格会保持一致。我们经常会遇到一些数据集,虽然在一定时期内出现小幅变动,但每个时间段的平均值确实保持不变。这种情况下,我们可以预测出第二天的价格大致和过去天数的价格平均值一致。这种将预期值等同于之前所有观测点的平均值的预测方法就叫简单平均法。
y ^ t + 1 = 1 x ∑ i = 1 t y i \hat{y}_{t+1}=\frac{1}{x}\sum_{i=1}^{t}{y_i} y^t+1=x1i=1∑tyi
y_hat_avg = test.copy()
y_hat_avg["avg_forecast"] = train["Count"].mean()
plt.figure(figsize=(12, 8))
plt.plot(train["Count"], label="Train")
plt.plot(test["Count"], label="Test")
plt.plot(y_hat_avg["avg_forecast"], label="Average Forecast")
plt.legend(loc="best")
plt.show()
用之前全部已知的值计算出它们的平均值,将它作为要预测的下一个值。当然这不会很准确,但这种预测方法在某些情况下效果是最好的。
该方法的均方根差为:109.88526527082863
from math import sqrt
from sklearn.metrics import mean_squared_error
rms = sqrt(mean_squared_error(test["Count"], y_hat_avg["avg_forecast"]))
print(rms)
109.88526527082863
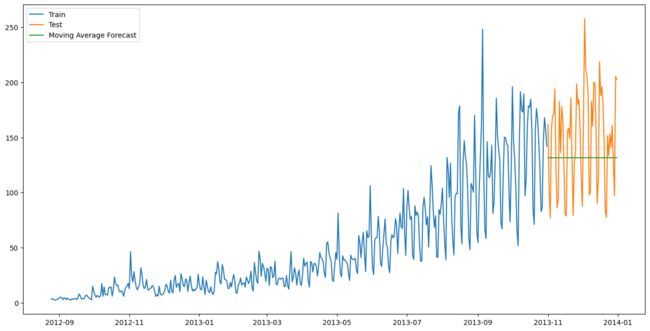
方法3:移动平均法
假设y轴表示某个物品的价格,x轴表示时间(天)。
物品价格在一段时间内大幅上涨,但后来又趋于平稳。我们也经常会遇到这种数据集,比如价格或销售额某段时间大幅上升或下降。如果我们这时用之前的简单平均法,就得使用所有先前数据的平均值,但在这里使用之前的所有数据是说不通的,因为用开始阶段的价格值会大幅影响接下来日期的预测值。因此,我们只取最近几个时期的价格平均值。很明显这里的逻辑是只有最近的值最要紧。这种用某些窗口期计算平均值的预测方法就叫移动平均法。
计算移动平均值涉及到一个有时被称为“滑动窗口”的大小值p。使用简单的移动平均模型,我们可以根据之前数值的固定有限数p的平均值预测某个时序中的下一个值。这样,对于所有的 i > p i>p i>p:
y ^ t + 1 = 1 p ( y t + y t − 1 + y t − 2 + ⋯ + y t − p + 1 ) \hat{y}_t+1=\frac{1}{p}(y_{t}+y_{t−1}+y_{t−2}+ \dots +y_{t−p+1}) y^t+1=p1(yt+yt−1+yt−2+⋯+yt−p+1)
移动平均法实际上很有效,特别是当你为时序选择了正确的p值时。(以下程序选择了60天作为窗口大小)
y_hat_avg = test.copy()
y_hat_avg["moving_avg_forecast"] = train["Count"].rolling(60).mean().iloc[-1]
plt.figure(figsize=(16, 8))
plt.plot(train["Count"], label="Train")
plt.plot(test["Count"], label="Test")
plt.plot(y_hat_avg["moving_avg_forecast"], label="Moving Average Forecast")
plt.legend(loc="best")
plt.show()
from math import sqrt
from sklearn.metrics import mean_squared_error
rms = sqrt(mean_squared_error(test["Count"], y_hat_avg["moving_avg_forecast"]))
print("此方法计算出来的均方根差为:", rms)
此方法计算出来的均方根差为: 46.72840725106963
可以看到,对于这个数据集,朴素法比简单平均法和移动平均法的表现要好。此外,我们还可以试试简单指数平滑法,它比移动平均法的一个进步之处就是相当于对移动平均法进行了加权。在上文移动平均法可以看到,我们对“p”中的观察值赋予了同样的权重。但是我们可能遇到一些情况,比如“p”中每个观察值会以不同的方式影响预测结果。将过去观察值赋予不同权重的方法就叫做加权移动平均法。加权移动平均法其实还是一种移动平均法,只是“滑动窗口期”内的值被赋予不同的权重,通常来讲,最近时间点的值发挥的作用更大了。
y ^ l = 1 m ( w 1 ∗ y i − 1 + w 2 ∗ y i − 2 + w 3 ∗ y i − 3 + ⋯ + w m ∗ y i − m ) \hat{y}_{l}=\frac{1}{m}(w_1∗y_{i−1}+w_2∗y_{i−2}+w_3∗y_{i−3}+ \dots +w_m∗y_{i−m}) y^l=m1(w1∗yi−1+w2∗yi−2+w3∗yi−3+⋯+wm∗yi−m)
这种方法并非选择一个窗口期的值,而是需要一列权重值(相加后为1)。例如,如果我们选择[0.40, 0.25, 0.20, 0.15]作为权值,我们会为最近的4个时间点分别赋给40%,25%,20%和15%的权重。
方法4:简单指数平滑法
我们注意到简单平均法和加权移动平均法在选取时间点的思路上存在较大的差异。我们就需要在这两种方法之间取一个折中的方法,在将所有数据考虑在内的同时也能给数据赋予不同非权重。例如,相比更早时期内的观测值,它会给近期的观测值赋予更大的权重。按照这种原则工作的方法就叫做简单指数平滑法。它通过加权平均值计算出预测值,其中权重随着观测值从早期到晚期的变化呈指数级下降,最小的权重和最早的观测值相关:
y ^ t + 1 ∣ t = α y t + α ( 1 − α ) y t − 1 + α ( 1 − α ) 2 y t − 2 + … \hat{y}_{t+1|t}=\alpha y_t+\alpha(1−\alpha)y_{t−1}+\alpha(1−\alpha)^2y_{t−2}+\dots y^t+1∣t=αyt+α(1−α)yt−1+α(1−α)2yt−2+…
其中 0 ≤ α ≤ 1 0\le \alpha\le1 0≤α≤1是平滑参数。对时间点t+1的单步预测值是时序 y 1 , … , y t y_1,\dots,y_t y1,…,yt的所有观测值的加权平均数。
权重下降的速率由参数 α \alpha α控制,预测值 y ^ t + 1 \hat{y}_{t+1} y^t+1是 α y t \alpha y_t αyt与 ( 1 − α ) y ^ t (1−\alpha) \hat{y}_{t} (1−α)y^t的和。(第一项后面提个公因式 1 − α 1-\alpha 1−α)
因此,它可以写为:
y ^ t + 1 ∣ t = α y t + ( 1 − α ) y ^ t ∣ t − 1 \hat{y}_{t+1|t}=\alpha y_t+(1-\alpha)\hat{y}_{t|t-1} y^t+1∣t=αyt+(1−α)y^t∣t−1
所以本质上,我们是用两个权重 α \alpha α和 1 − α 1-\alpha 1−α得到一个加权移动平均值。我们可以看到 y ^ t ∣ t − 1 \hat{y}_{t|t-1} y^t∣t−1和 1 − α 1-\alpha 1−α相乘,让表达式呈递进形式,这也是该方法被称为“指数”的原因。时间t+1处的预测值为最近观测值 y t y_t yt和最近预测值 y t ∣ t − 1 y_{t|t-1} yt∣t−1之间的加权平均值。
平面预测
简单的指数平滑具有一个“平坦”的预测函数:
y ^ t + h ∣ t = y ^ t + 1 ∣ t \hat{y}_{t+h|t}=\hat{y}_{t+1|t} y^t+h∣t=y^t+1∣t
也就是说,所有预测值都相同,等于最后一个级别分量。请记住,只有时间序列没有趋势或季节性分量时,这些预测才适用。
优化
每个指数平滑方法在应用时都需要选择平滑参数和初始值。特别是对于简单的指数平滑,我们需要选择 α \alpha α 和 l 0 l_0 l0 的值。只要我们知道这些值,所有的预测值都可以从数据中计算出来。对于其他的方法,通常有多个平滑参数和多个初始分量要选择。
在某些情况下,平滑参数可以进行主观选择—预测者根据以前的经验设定平滑参数的值。然而,一种更可靠和客观的获得未知参数值的方法是从观测数据中估计它们。
任何指数平滑方法的未知参数和初始值也可以通过最小化SSE来进行估计。
from statsmodels.tsa.api import SimpleExpSmoothing
y_hat_avg = test.copy()
fit = SimpleExpSmoothing(np.asarray(train["Count"])).fit(
smoothing_level=0.6, optimized=False
)
y_hat_avg["SES"] = fit.forecast(len(test))
print(y_hat_avg)
plt.figure(figsize=(16, 8))
plt.plot(train["Count"], label="Train")
plt.plot(test["Count"], label="Test")
plt.plot(y_hat_avg["SES"], label="SES")
plt.legend(loc="best")
plt.show()
ID Count SES
Timestamp
2013-11-01 10403.5 161.583333 147.107374
2013-11-02 10427.5 103.083333 147.107374
2013-11-03 10451.5 76.833333 147.107374
2013-11-04 10475.5 156.416667 147.107374
2013-11-05 10499.5 169.750000 147.107374
... ... ... ...
2013-12-27 11747.5 161.166667 147.107374
2013-12-28 11771.5 128.500000 147.107374
2013-12-29 11795.5 97.083333 147.107374
2013-12-30 11819.5 205.333333 147.107374
2013-12-31 11843.5 202.500000 147.107374
[61 rows x 3 columns]
from math import sqrt
from sklearn.metrics import mean_squared_error
rms = sqrt(mean_squared_error(test["Count"], y_hat_avg["SES"]))
print("上述方法计算出来的均方根差为:", rms)
上述方法计算出来的均方根差为: 43.357625225228155
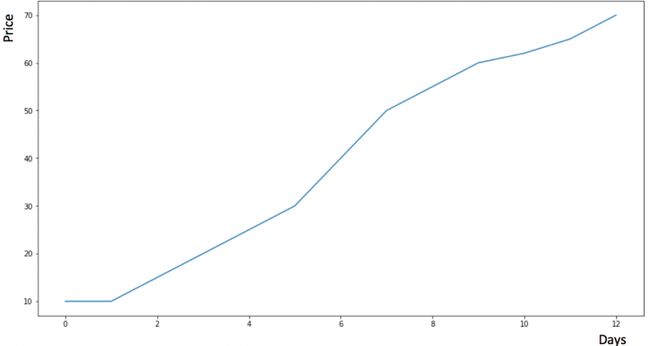
方法5:霍尔特(Holt)线性趋势法
假设y轴表示某个物品的价格,x轴表示时间(天)。
如果物品的价格是不断上涨的(见上图),我们上面的方法并没有考虑这种趋势,即我们在一段时间内观察到的价格的总体模式。在上图例子中,我们可以看到物品的价格呈上涨趋势。虽然上面这些方法都可以应用于这种趋势,但我们仍需要一种方法可以在无需假设的情况下,准确预测出价格趋势。这种考虑到数据集变化趋势的方法就叫做霍尔特线性趋势法。
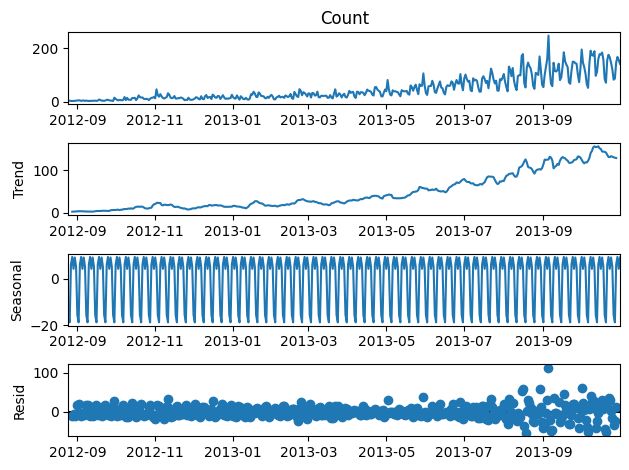
每个时序数据集可以分解为相应的几个部分:趋势(Trend),季节性(Seasonal)和残差(Residual)。任何呈现某种趋势的数据集都可以用霍尔特线性趋势法用于预测。
import statsmodels.api as sm
sm.tsa.seasonal_decompose(train["Count"]).plot()
result = sm.tsa.stattools.adfuller(train["Count"])
print(result)
plt.show()
(0.30658561505474313, 0.9776446211118099, 16, 416, {'1%': -3.4461675720270404, '5%': -2.8685128587855955, '10%': -2.5704843086630915}, 3389.3168092754736)
我们从图中可以看出,该数据集呈上升趋势。因此我们可以用霍尔特线性趋势法预测未来价格。该算法包含三个方程:一个水平方程,一个趋势方程,一个方程将二者相加以得到预测值 y ^ \hat{y} y^:
F o r e c a s t : y ^ t + h ∣ t = l t + h b t Forecast:\hat{y}_{t+h|t}=l_t+hb_t Forecast:y^t+h∣t=lt+hbt
L e v e l : l t = α y t + ( 1 − α ) ( l t − 1 + b t − 1 ) Level: l_t=\alpha y_t+(1-\alpha)(l_{t-1}+b_{t-1}) Level:lt=αyt+(1−α)(lt−1+bt−1)
T r e n d : b t = β ∗ ( l t − l t − 1 ) + ( 1 − β ∗ ) b t − 1 Trend :b_t=\beta^{*}(l_t-l_{t-1})+(1-\beta^{*})b_{t-1} Trend:bt=β∗(lt−lt−1)+(1−β∗)bt−1
初始化 l 0 l_0 l0和 b 0 b_0 b0
其中 l t l_t lt 表示在t时刻该时间序列的水平的估计值, b t b_t bt表示该时间序列在t时刻的趋势(斜率)的估计, α \alpha α是水平 0 ≤ α ≤ 1 0\le \alpha \le 1 0≤α≤1的平滑参数, β ∗ \beta^* β∗是趋势 0 ≤ β ∗ ≤ 1 0\le \beta^* \le 1 0≤β∗≤1的平滑参数。
与简单的指数平滑一样,这里的水平方程表明 l t l_t lt是观测值 y t y_t yt和t时刻的向前一步训练预测值的加权平均值,这里由 l t − 1 + b t − 1 l_{t-1}+b_{t-1} lt−1+bt−1给出。趋势方程表明, b t b_t bt是基于 l t − l t − 1 l_t-l_{t-1} lt−lt−1和前一个趋势的估计值 b t − 1 b_{t-1} bt−1在 t时刻的估计值的加权平均值。
这里的预测函数不再平坦,而是有趋势的。向前h步预测值等于上一次估计的水平值加上前一个估计的趋势值的 h倍。因此,预测值是一个关于h的线性函数。
我们将这两个方程相加,得出一个预测函数。我们也可以将两者相乘而不是相加得到一个乘法预测方程。当趋势呈线性增加和下降时,我们用相加得到的方程;当趋势呈指数级增加或下降时,我们用相乘得到的方程。实践操作显示,用相乘得到的方程,预测结果会更稳定,但用相加得到的方程,更容易理解。
from statsmodels.tsa.api import Holt
y_hat_avg = test.copy()
fit = Holt(np.asarray(train["Count"])).fit(smoothing_level=0.3, smoothing_slope=0.1)
y_hat_avg["Holt_linear"] = fit.forecast(len(test))
plt.figure(figsize=(16, 8))
plt.plot(train["Count"], label="Train")
plt.plot(test["Count"], label="Test")
plt.plot(y_hat_avg["Holt_linear"], label="Holt_linear")
plt.legend(loc="best")
plt.show()
C:\Users\suny\AppData\Local\Temp\ipykernel_15144\3213697839.py:5: FutureWarning: the 'smoothing_slope'' keyword is deprecated, use 'smoothing_trend' instead.
fit = Holt(np.asarray(train['Count'])).fit(smoothing_level=0.3, smoothing_slope=0.1)
from math import sqrt
from sklearn.metrics import mean_squared_error
rms = sqrt(mean_squared_error(test["Count"], y_hat_avg["Holt_linear"]))
print(rms)
43.056259611507286
这种方法能够准确地显示出趋势,因此比前面的几种模型效果更好。如果调整一下参数,结果会更好。
方法6:Holt-Winters季节性预测模型
在应用这种算法前,我们先介绍一个新术语。假如有家酒店坐落在半山腰上,夏季的时候生意很好,顾客很多,但每年其余时间顾客很少。因此,每年夏季的收入会远高于其它季节,而且每年都是这样,那么这种重复现象叫做“季节性”(Seasonality)。如果数据集在一定时间段内的固定区间内呈现相似的模式,那么该数据集就具有季节性。
之前讨论的模型在预测时并没有考虑到数据集的季节性,因此我们需要一种能考虑这种因素的方法。应用到这种情况下的算法就叫做Holt-Winters季节性预测模型,它是一种三次指数平滑预测,其背后的理念就是除了水平和趋势外,还将指数平滑应用到季节分量上。
Holt-Winters季节性预测模型由预测函数和三次平滑函数——一个是水平函数 l t l_t lt,一个是趋势函数 b t b_t bt,一个是季节分量 s t s_t st,以及平滑参数 α \alpha α, β ∗ \beta^* β∗和 γ \gamma γ。
加法分量形式
y ^ t + h ∣ t = l t + h b t + s t − m + h m + \hat{y}_{t+h|t}=l_t+hb_t+s_{t-m+h_m^+} y^t+h∣t=lt+hbt+st−m+hm+
l t = α ( y t − s t − m ) + ( 1 − α ) ( l ( t − 1 ) + b t 1 ) l_t=\alpha(y_t-s_{t-m})+(1-\alpha)(l_(t-1)+b_{t_1}) lt=α(yt−st−m)+(1−α)(l(t−1)+bt1)
b t = β ∗ ( l t − l t − 1 ) + ( 1 − β ∗ ) ( b t − 1 ) b_t=\beta^*(l_t-l_{t-1})+(1-\beta^*)(b_{t-1}) bt=β∗(lt−lt−1)+(1−β∗)(bt−1)
s t = γ ( y t − l t − 1 − b t − 1 ) + ( 1 − γ ) s t − m s_t=\gamma(y_t-l_{t-1}-b_{t-1})+(1-\gamma)s_{t-m} st=γ(yt−lt−1−bt−1)+(1−γ)st−m
初始化 α 、 β 、 γ \alpha、\beta、\gamma α、β、γ和 l 0 、 b 0 、 s 0 … s m l_0、b_0、s_0 \dots s_m l0、b0、s0…sm
m来表示季节频率,即一年中包含的季节数。平函数为季节性调整的观测值和时间点t处非季节预测之间的加权平均值。趋势函数和霍尔特线性方法中的含义相同。季节函数为当前季节指数和去年同一季节的季节性指数之间的加权平均值。
在本算法,我们同样可以用相加和相乘的方法。当季节性变化大致相同时,优先选择相加方法,而当季节变化的幅度与各时间段的水平成正比时,优先选择相乘的方法。
from statsmodels.tsa.api import ExponentialSmoothing
y_hat_avg = test.copy()
fit1 = ExponentialSmoothing(
np.asarray(train["Count"]),
seasonal_periods=7,
trend="add",
seasonal="add",
).fit()
y_hat_avg["Holt_Winter"] = fit1.forecast(len(test))
plt.figure(figsize=(16, 8))
plt.plot(train["Count"], label="Train")
plt.plot(test["Count"], label="Test")
plt.plot(y_hat_avg["Holt_Winter"], label="Holt_Winter")
plt.legend(loc="best")
plt.show()
from math import sqrt
from sklearn.metrics import mean_squared_error
rms = sqrt(mean_squared_error(test["Count"], y_hat_avg["Holt_Winter"]))
print(rms)
25.264160714051183
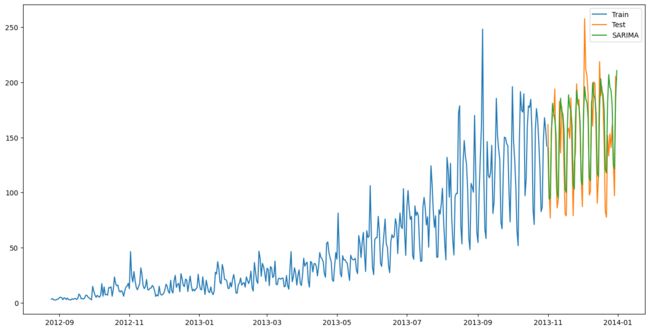
方法7:自回归移动平均模型(ARIMA)
具体参看arima文档
另一个场景的时序模型是自回归移动平均模型(ARIMA)。指数平滑模型都是基于数据中的趋势和季节性的描述,而自回归移动平均模型的目标是描述数据中彼此之间的关系。ARIMA的一个优化版就是季节性ARIMA。它像Holt-Winters季节性预测模型一样,也把数据集的季节性考虑在内。
import statsmodels.api as sm
y_hat_avg = test.copy()
fit1 = sm.tsa.statespace.SARIMAX(train.Count, order=(2, 1, 4), seasonal_order=(0, 1, 1, 7)).fit()
y_hat_avg['SARIMA'] = fit1.predict(start="2013-11-1", end="2013-12-31", dynamic=True)
plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['SARIMA'], label='SARIMA')
plt.legend(loc='best')
plt.show()
D:\soft\tool\Anaconda3\envs\py38\lib\site-packages\statsmodels\base\model.py:604: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
warnings.warn("Maximum Likelihood optimization failed to "
from sklearn.metrics import mean_squared_error
from math import sqrt
rms = sqrt(mean_squared_error(test['Count'], y_hat_avg['SARIMA']))
print(rms)
26.069547371326845