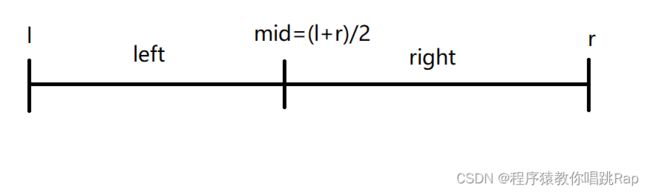【算法基础】基础算法之排序
PREFACE
欢迎各位→点赞 + 收藏⭐ + 评论
系列专栏: 算法
种一棵树最好是十年前其次是现在
目录
1.快排
步骤
思路方法
题目1:快速排序
参考代码
题目2:第k个数
参考代码
快排的注意点
1.快排模板
2.快排总结
2.归并排序
步骤
思路方法
题目:归并排序
参考代码
归并模板
1.快排
-
步骤
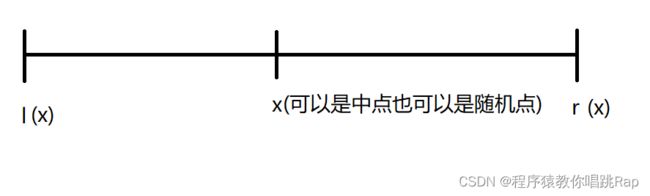
1.确定分界点:分界点一般取左端点,右端点,中点或者随机点
2.调整区间:比如说分界点为x,把小于x分在左边区间,把大于x分在右边区间
3.递归处理左右两段
-
思路方法
法一:
1.开两个数组:a[ ], b[ ].2.扫描整个区间从最左端到最右端,如果比x小就放到a数组里面,比x大就放到b数组里面
3.之后再把a数组和b数组合并成一个数组
法二:
1.定义两个指针i,j
2.把i放在left处,j放在right处
3.如果i所在的位置小于x,此时i++,若大于x,i停下来,j所在的位置大于x,此时j--,若小于x,j停下来。最后再把i,j交换一下,接着如此循环下去
4.循环结束条件为i与j相遇或者错位为止
显然法二相较于法一更优,下面根据例题来进行法二的代码实现:
-
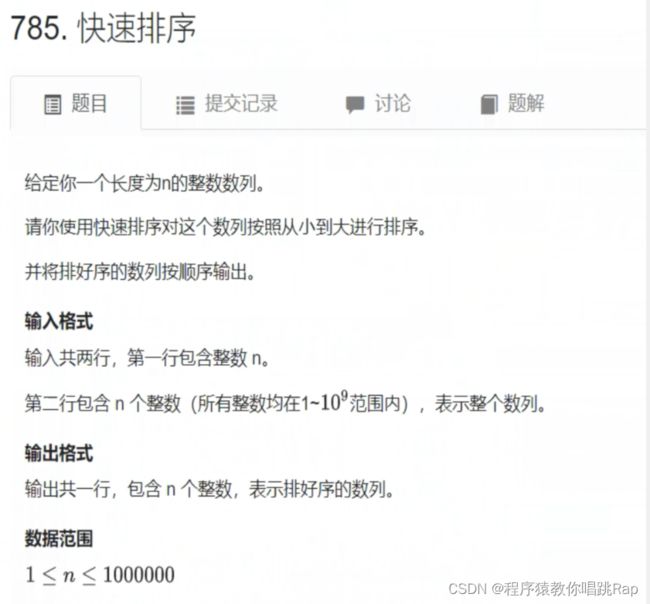
题目1:快速排序
-
参考代码
#include
using namespace std;
const int N = 1e6 + 10;
int n;
int q[N];
void quick_sort(int q[], int l, int r)
{
if (l >= r)
{
return;
}
int x = q[l], i = l - 1, j = r + 1;
while (i < j)
{
do
{
i++;
} while (q[i] < x);
do
{
j--;
} while (q[j] > x);
if (i < j)
swap(q[i], q[j]);
}
quick_sort(q, l, j);
quick_sort(q, j + 1, r);
//用这种模板时,x不能取右边界
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i++)
{
scanf("%d", &q[i]);
}
quick_sort(q, 0, n - 1);
for (int i = 0; i < n; i++)
{
printf("%d ", q[i]);
}
return 0;
} 快排题目代码人工动态展示过程:
RPReplay_Final1674209649(1)
-
题目2:第k个数
参考代码
#include
using namespace std;
const int N = 1e6 + 10;
int n,k;
int q[N];
void quick_sort(int q[], int l, int r)
{
if (l >= r)
{
return;//边界
}
int x = q[l+r>>1], i = l - 1, j = r + 1;
while (i < j)
{
do
{
i++;
} while (q[i] < x);
do
{
j--;
} while (q[j] > x);
if (i < j)
swap(q[i], q[j]);
}
quick_sort(q, l, j);
quick_sort(q, j + 1, r);
}
int main()
{
scanf("%d %d", &n,&k);
for (int i = 0; i < n; i++)
{
scanf("%d", &q[i]);
}
quick_sort(q, 0, n - 1);
for (int i = 0; i < n; i++)
{
if (i + 1 == k)
printf("%d\n", q[i]);
}
return 0;
} 快排的注意点
1.快排模板
void quick_sort(int q[], int l, int r) { //递归的终止情况 if(l >= r) return; //第一步:分成子问题 int i = l - 1, j = r + 1, x = q[l + r >> 1]; while(i < j) { do i++; while(q[i] < x); do j--; while(q[j] > x); if(i < j) swap(q[i], q[j]); } //第二步:递归处理子问题 quick_sort(q, l, j), quick_sort(q, j + 1, r); //第三步:子问题合并.快排这一步不需要操作,但归并排序的核心在这一步骤 }2.快排总结
2.归并排序
-
步骤
2.递归排序left,right
3.归并(合二为一)
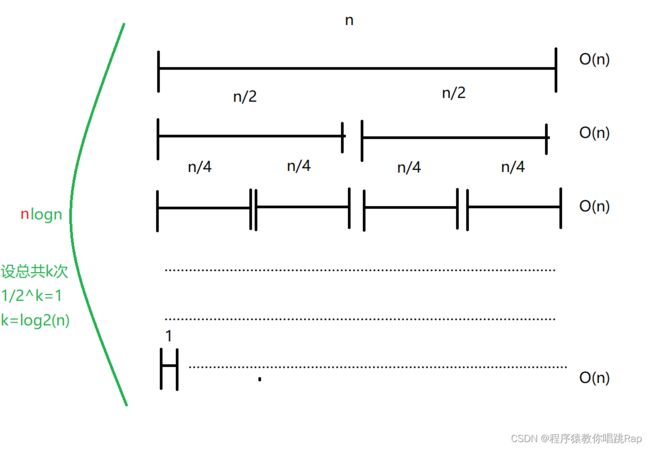
关于归并排序的时间复杂度
-
思路方法
1.有数组 q, 左端点 l, 右端点 r
2.确定划分边界 mid=(left+right)/2
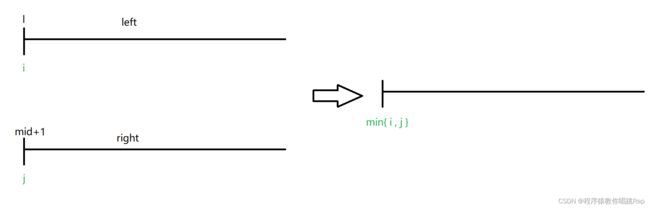
3.递归处理子问题 q[l..mid], q[mid+1..r]
4.合并子问题
- 主体并:至少有一个小数组添合加到新数组中
收尾:可能存在的剩下的一个小数组的尾部直接添加到新数组中
复制回来:新数组覆盖原数组
-
题目1:归并排序
-
参考代码
#include
using namespace std;
const int N = 1e6 + 10;
int n;
int q[N], tmp[N];
void merge_sort(int q[], int l, int r)
{
if (l >= r)
{
return;
}
int mid = (l + r) >> 1;
merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
{
if (q[i] <= q[j])
{
tmp[k++] = q[i++];
}
else
{
tmp[k++] = q[j++];
}
}
while (i <= mid)
{
tmp[k++] = q[i++];
}
while (j <= r)
{
tmp[k++] = q[j++];
}
for (i = l, j = 0; i <= r; i++, j++)
{
q[i] = tmp[j];
}
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i++)
{
scanf("%d", &q[i]);
}
merge_sort(q, 0, n - 1);
for (int i = 0; i < n; i++)
{
printf("%d ", q[i]);
}
return 0;
} -
题目2:逆序对的数量
-
参考代码
#include
using namespace std;
typedef long long LL;
const int N=1e6+10;
int n;
int q[N],tmp[N];
LL merge_sort(int l,int r)
{
if(l>=r) return 0;
int mid=l+r>>1;
LL res=merge_sort(l,mid)+merge_sort(mid+1,r);
//归并的过程
int k=0,i=l,j=mid+1;
while(i<=mid&&j<=r)
{
if(q[i]<=q[j])
tmp[k++]=q[i++];
else
{
tmp[k++]=q[j++];
res+=mid-i+1;
}
}
//扫尾
while(i<=mid) tmp[k++]=q[i++];
while(j<=r) tmp[k++]=q[j++];
//物归原主
for(int i=l,j=0;i<=r;i++,j++)
{
q[i]=tmp[j];
}
return res;
}
int main()
{
cin>>n;
for(int i=0;i>q[i];
cout< -
归并模板
归并属于分治算法,有三个步骤:
void merge_sort(int q[], int l, int r) { //递归的终止情况 if(l >= r) return; //第一步:分成子问题 int mid = l + r >> 1; //第二步:递归处理子问题 merge_sort(q, l, mid ), merge_sort(q, mid + 1, r); //第三步:合并子问题 int k = 0, i = l, j = mid + 1, tmp[r - l + 1]; while(i <= mid && j <= r) if(q[i] <= q[j]) tmp[k++] = q[i++]; else tmp[k++] = q[j++]; while(i <= mid) tmp[k++] = q[i++]; while(j <= r) tmp[k++] = q[j++]; for(k = 0, i = l; i <= r; k++, i++) q[i] = tmp[k]; }