LeetCode算法小抄-- N 叉树 和 洗牌算法

⚠申明： 未经许可，禁止以任何形式转载，若要引用，请标注链接地址。 全文共计3605字，阅读大概需要3分钟
更多学习内容， 欢迎关注【文末】我的个人微信公众号：不懂开发的程序猿
个人网站：https://jerry-jy.co/

N 叉树

341. 扁平化嵌套列表迭代器

给你一个嵌套的整数列表 nestedList 。每个元素要么是一个整数，要么是一个列表；该列表的元素也可能是整数或者是其他列表。请你实现一个迭代器将其扁平化，使之能够遍历这个列表中的所有整数。

实现扁平迭代器类 NestedIterator ：

• NestedIterator(List nestedList) 用嵌套列表 nestedList 初始化迭代器。
• int next() 返回嵌套列表的下一个整数。
• boolean hasNext() 如果仍然存在待迭代的整数，返回 true ；否则，返回 false 。

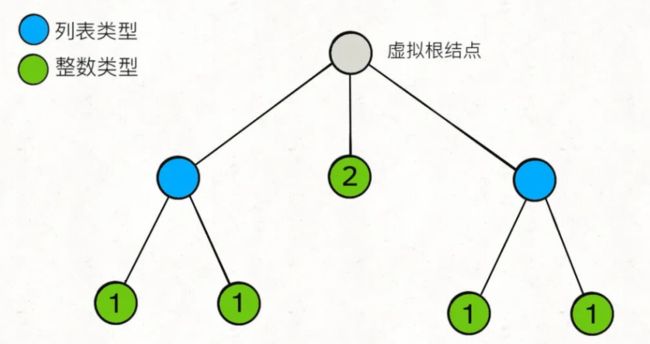
比如说输入是[[1,1],2,[1,1]]，其实就是如下树状结构

把一个NestedInteger扁平化对吧？这就等价于遍历一棵 N 叉树的所有「叶子节点」？

/**
 * // This is the interface that allows for creating nested lists.
 * // You should not implement it, or speculate about its implementation
 * public interface NestedInteger {
 *
 *     // @return true if this NestedInteger holds a single integer, rather than a nested list.
 *     public boolean isInteger();
 *
 *     // @return the single integer that this NestedInteger holds, if it holds a single integer
 *     // Return null if this NestedInteger holds a nested list
 *     public Integer getInteger();
 *
 *     // @return the nested list that this NestedInteger holds, if it holds a nested list
 *     // Return empty list if this NestedInteger holds a single integer
 *     public List getList();
 * }
 */
public class NestedIterator implements Iterator<Integer> {

    private LinkedList<NestedInteger> list; 
    
    public NestedIterator(List<NestedInteger> nestedList) {
        // 不直接用 nestedList 的引用，是因为不能确定它的底层实现
        // 必须保证是 LinkedList，否则下面的 addFirst 会很低效
        list = new LinkedList<>(nestedList);
    }

    @Override
    public Integer next() {
        // hasNext 方法保证了第一个元素一定是整数类型
        return list.remove(0).getInteger();
    }

    @Override
    public boolean hasNext() {
        // 循环拆分列表元素，直到列表第一个元素是整数类型
        while (!list.isEmpty() && !list.get(0).isInteger()) {
            // 当列表开头第一个元素是列表类型时，进入循环
            List<NestedInteger> first = list.remove(0).getList();
            // 将第一个列表打平并按顺序添加到开头
            for (int i = first.size() - 1; i >= 0; i--) {
                list.addFirst(first.get(i));
            }
        }
        return !list.isEmpty();        
    }
}

/**
 * Your NestedIterator object will be instantiated and called as such:
 * NestedIterator i = new NestedIterator(nestedList);
 * while (i.hasNext()) v[f()] = i.next();
 */

洗牌算法

又被称为「随机乱置算法」

怎么能证明你的算法是「真的乱」呢？

1. 什么叫做「真的乱」？

2. 设计怎样的算法来打乱数组才能做到「真的乱」？

此类算法都是靠随机选取元素交换来获取随机性，直接看伪代码，该算法有 4 种形式，都是正确的：

// 得到一个在闭区间 [min, max] 内的随机整数
int randInt(int min, int max);

// 第一种写法
void shuffle(int[] arr) {
    int n = arr.length();
    /******** 区别只有这两行 ********/
    for (int i = 0 ; i < n; i++) {
        // 从 i 到最后随机选一个元素
        int rand = randInt(i, n - 1);
        /*************************/
        swap(arr[i], arr[rand]);
    }
}

// 第二种写法
    for (int i = 0 ; i < n - 1; i++)
        int rand = randInt(i, n - 1);

// 第三种写法
    for (int i = n - 1 ; i >= 0; i--)
        int rand = randInt(0, i);

// 第四种写法
    for (int i = n - 1 ; i > 0; i--)
        int rand = randInt(0, i);

洗牌算法正确性的准则：产生的结果必须有 n! 种可能，否则就是错误的。

蒙特卡罗方法验证正确性

洗牌算法，或者说随机乱置算法的正确性衡量标准是：对于每种可能的结果出现的概率必须相等，也就是说要足够随机。

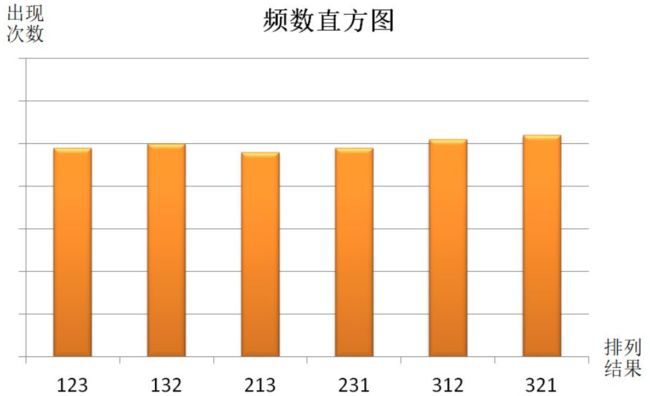
第一种思路，我们把数组 arr 的所有排列组合都列举出来，做成一个直方图（假设 arr = {1,2,3}）

每次进行洗牌算法后，就把得到的打乱结果对应的频数加一，重复进行 100 万次，如果每种结果出现的总次数差不多，那就说明每种结果出现的概率应该是相等的。

伪代码

void shuffle(int[] arr);

// 蒙特卡罗
int N = 1000000;
HashMap count; // 作为直方图
for (i = 0; i < N; i++) {
    int[] arr = {1,2,3};
    shuffle(arr);
    // 此时 arr 已被打乱
    count[arr] += 1；
}
for (int feq : count.values()) 
    print(feq / N + " "); // 频率

arr 的全部排列有 n! 种（n 为 arr 的长度），如果 n 比较大，空间复杂度恒很高

第二种思路，可以这样想，arr 数组中全都是 0，只有一个 1。我们对 arr 进行 100 万次打乱，记录每个索引位置出现 1 的次数，如果每个索引出现 1 的次数差不多，也可以说明每种打乱结果的概率是相等的

void shuffle(int[] arr);

// 蒙特卡罗方法
int N = 1000000;    
int[] arr = {1,0,0,0,0};
int[] count = new int[arr.length];
for (int i = 0; i < N; i++) {
    shuffle(arr); // 打乱 arr
    for (int j = 0; j < arr.length; j++) 
        if (arr[j] == 1) {
            count[j]++;
            break;
        }
}
for (int feq : count) 
    print(feq / N + " "); // 频率

这种思路也是可行的，而且避免了阶乘级的空间复杂度，但是多了嵌套 for 循环，时间复杂度高一点

–end–