Matlab群体智能优化算法之鹈鹕优化算法(POA)
Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications
参考文献:Trojovský P, Dehghani M. Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications[J]. Sensors, 2022, 22(3): 855.
注:仅记录学习,如有侵权,联系删除。
The behavior and strategy of pelicans when hunting is an intelligent process that has made these birds skilled hunters. The main inspiration in the design of the proposed POAis originated from the modeling of the mentioned strategy.
1、初始化
X代表整个鹈鹕种群,每个 X i X_{i} Xi都是都是给定问题的一个候选解。
F代表适应度函数值。
X = [ X 1 ⋮ X i ⋮ X N ] N × m = [ x 1 , 1 ⋯ x 1 , j ⋯ x 1 , m ⋮ ⋱ ⋮ ⋮ x i , 1 ⋯ x i , j ⋯ x i , m ⋮ ⋮ ⋱ ⋮ x N , 1 ⋯ x N , j ⋯ x N , m ] N × m X=\left[\begin{array}{c} X_{1} \\ \vdots \\ X_{i} \\ \vdots \\ X_{N} \end{array}\right]_{N \times m}=\left[\begin{array}{ccccc} x_{1,1} & \cdots & x_{1, j} & \cdots & x_{1, m} \\ \vdots & \ddots & \vdots & & \vdots \\ x_{i, 1} & \cdots & x_{i, j} & \cdots & x_{i, m} \\ \vdots & & \vdots & \ddots & \vdots \\ x_{N, 1} & \cdots & x_{N, j} & \cdots & x_{N, m} \end{array}\right]_{N \times m} X=⎣⎢⎢⎢⎢⎢⎢⎡X1⋮Xi⋮XN⎦⎥⎥⎥⎥⎥⎥⎤N×m=⎣⎢⎢⎢⎢⎢⎢⎡x1,1⋮xi,1⋮xN,1⋯⋱⋯⋯x1,j⋮xi,j⋮xN,j⋯⋯⋱⋯x1,m⋮xi,m⋮xN,m⎦⎥⎥⎥⎥⎥⎥⎤N×m
F = [ F 1 ⋮ F i ⋮ F N ] N × 1 = [ F ( X 1 ) ⋮ F ( X i ) ⋮ F ( X N ) ] N × 1 F=\left[\begin{array}{c} F_{1} \\ \vdots \\ F_{i} \\ \vdots \\ F_{N} \end{array}\right]_{N \times 1}=\left[\begin{array}{c} F\left(X_{1}\right) \\ \vdots \\ F\left(X_{i}\right) \\ \vdots \\ F\left(X_{N}\right) \end{array}\right]_{N \times 1} F=⎣⎢⎢⎢⎢⎢⎢⎡F1⋮Fi⋮FN⎦⎥⎥⎥⎥⎥⎥⎤N×1=⎣⎢⎢⎢⎢⎢⎢⎡F(X1)⋮F(Xi)⋮F(XN)⎦⎥⎥⎥⎥⎥⎥⎤N×1
x i , j = l j + rand ⋅ ( u j − l j ) , i = 1 , 2 , … , N , j = 1 , 2 , … , m x_{i, j}=l_{j}+\text { rand } \cdot\left(u_{j}-l_{j}\right), i=1,2, \ldots, N, j=1,2, \ldots, m xi,j=lj+ rand ⋅(uj−lj),i=1,2,…,N,j=1,2,…,m
式中: x i , j x_{i, j} xi,j代表第i个鹈鹕的第j个变量的值;N是种群大小;m是维度;rand代表[0,1]之间的随机数; l j l_{ j} lj代表下限; u j u_{ j} uj代表上限。
2、位置更新方式
 2.1 探索阶段
2.1 探索阶段
x i , j P 1 = { x i , j + rand ⋅ ( p j − I ⋅ x i , j ) , F p < F i x i , j + rand ⋅ ( x i , j − p j ) , else x_{i, j}^{P_{1}}= \begin{cases}x_{i, j}+\text { rand } \cdot\left(p_{j}-I \cdot x_{i, j}\right), & F_{p}
式中: p j p_{j} pj是第j个维度上的猎物位置, F p F_{p} Fp是其目标函数值; I I I是随机数字,可以取1或2,当 I I I=2时,可以增加每个个体的位移,使得其进入搜索空间的新区域。
探索结束后,判断新位置的目标函数值和猎物的目标函数值谁大谁小,谁小取谁,更新方式如下:
X i = { X i P 1 , F i P 1 < F i X i , else X_{i}=\left\{\begin{array}{cc} X_{i}^{P_{1}}, & F_{i}^{P_{1}}
2.2 开发阶段
x i , j P 2 = x i , j + R ⋅ ( 1 − t T ) ⋅ ( 2 ⋅ rand − 1 ) ⋅ x i , j x_{i, j}^{P_{2}}=x_{i, j}+R \cdot\left(1-\frac{t}{T}\right) \cdot(2 \cdot \text { rand }-1) \cdot x_{i, j} xi,jP2=xi,j+R⋅(1−Tt)⋅(2⋅ rand −1)⋅xi,j
式中:R=0.2,常数; t t t是当前迭代次数; T T T是最大迭代次数。
X i = { X i P 2 , F i P 2 < F i X i , else X_{i}=\left\{\begin{array}{cc} X_{i}^{P_{2}}, & F_{i}^{P_{2}}
3、重复步骤
在所有个体经过第一和第二阶段更新后,基于种群的新状态和目标函数的值,到目前位置的最佳候选方案将被更新。算法进入下一次迭代,基于上述位置更新方式的4个公式重复执行,直到完全结束。结束的方式可以被设置好的误差要求截断或者终止于迭代次数。最后,最佳候选方案即为给定问题的准最优解。
4、复杂度
O ( N + T − ( 1 + m ) − ( 1 + 2 − N ) ) O(N+T-(1+m)-(1+2-N)) O(N+T−(1+m)−(1+2−N))
5、流程图
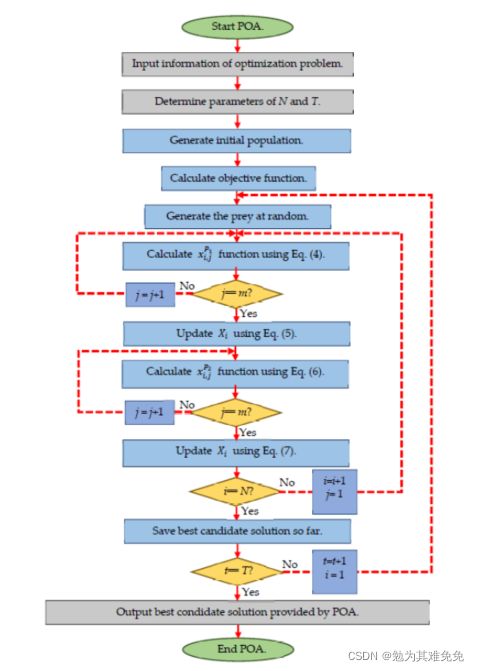
6、伪代码

7、测试函数

8、结果图
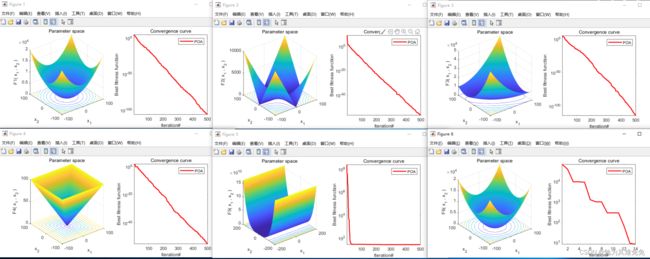
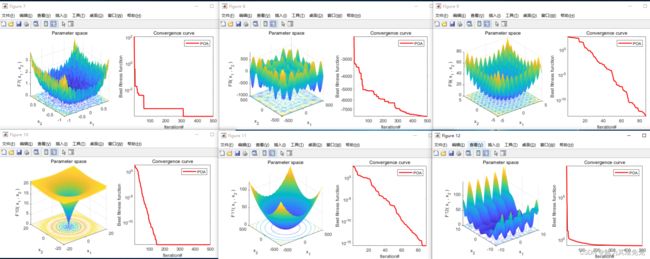
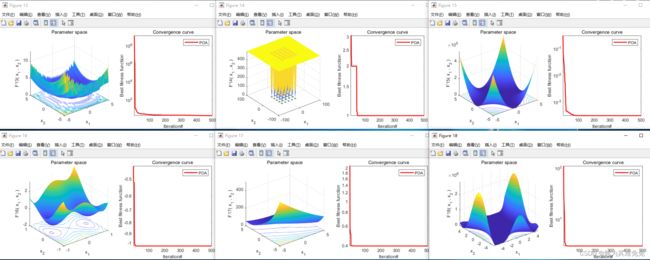
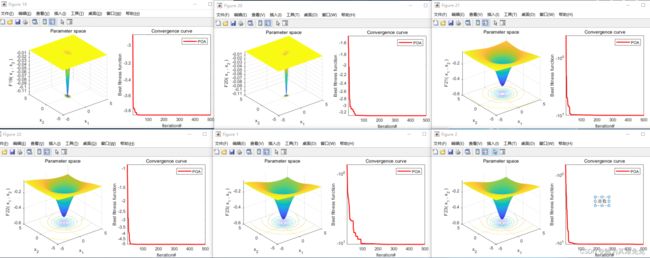
注:暂时没有和其他算法对比。原文和MPA、TSA、WOA、GWO、TLBO、GSA、PSO、GA进行了对比。后续根据个人需求选择算法进行对比吧。