排序-时间复杂度

技巧：先处理 内层 一次排序，在处理外面

直接插入排序

升序
最坏(遇到降序)：O(N^2) 等差数列 1+2+3+…+(n-1) = (n^2-n)/2
最好(有序) O(N)

希尔排序

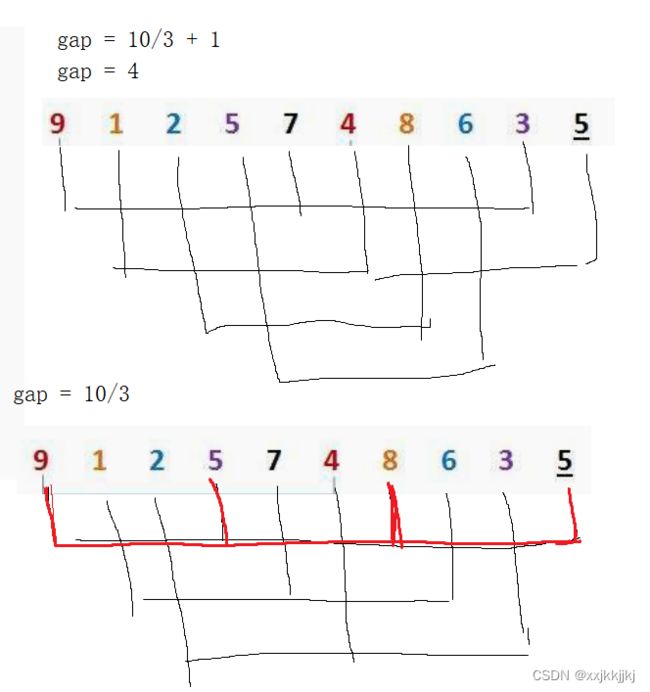
gap 任何数字/2都是=1
gap/3 +1 保证gap最后是1

gap是多少 就分了多少组,每组数据可能少一点，但是肯定能分成gap组，前提是gapn是不够分成gap组，比如gap=4,n=3分不成

时间复杂度分析

外层while(gap>1)----LogN
里面gap 很大 可以算出精确的2n 认为是N
gap=1 n 认为是N
gap变小过程中 ，N的变化

这里面就无法算出精确的了
结论：N^1.3

//N^1.3
void ShellSort(int* a, int n)
{
	//gap>1 预排序
	//gap == 1 直接插入排序
	int gap = n;
	while (gap > 1)
	{
		//gap /= 2;
		gap = gap / 3 + 1;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;//tmp>a[end] 结束
				}
			}
			a[end + gap] = tmp;
		}
		//PrintArray(a, n);
	}

}

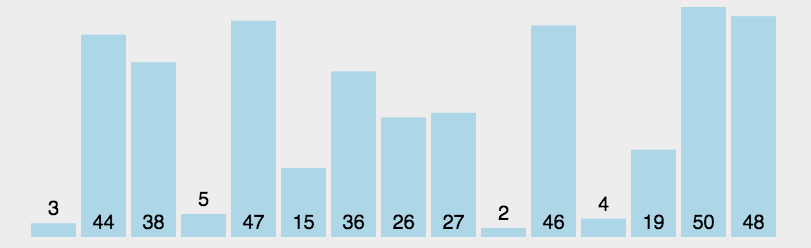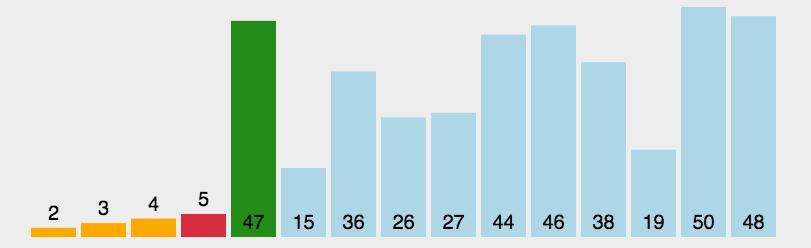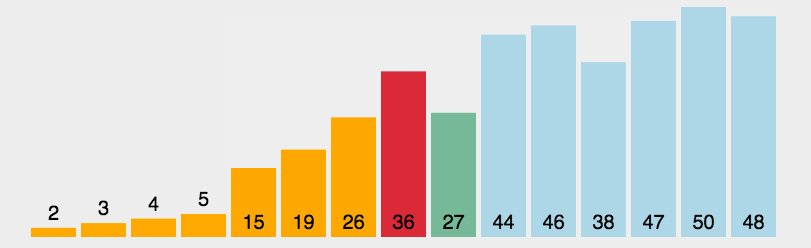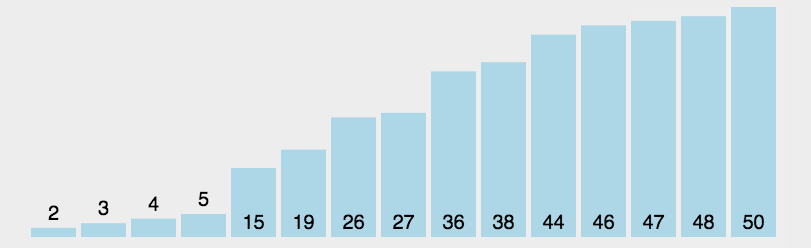
选择排序

最烂的排序

最坏：N^2 N N-2 N-4 … 等差数列
最好：N^2
N-2还是优化后的，遍历一遍可以选出最大最小
不优化每次选出最小，选出一个

//最坏：N^2  N N-2 N-4 ...等差数列
//最好：N^2
void SelectSort(int* a, int n)
{
	int left = 0, right = n - 1;
	while (left < right)
	{
		int min = left, max = left;
		for (int i = left + 1; i <= right; i++)
		{
			if (a[i] < a[min])
			{
				min = i;
			}
			if (a[i] > a[max])
			{
				max = i;
			}
		}
		Swap(&a[left], &a[min]);
		if (left == max)
		{
			max = min;
		}
		Swap(&a[right], &a[max]);

		left++;
		right--;
	}
	
}

堆排序

O(NlogN)

交换排序

交换排序（冒泡，快排） 是把数据进行交换，也就是Swap() 就像不能直接站到同学的脑袋上去

冒泡排序

如果不加flag优化 时间复杂度 O(N^2) 等差数列 N-1 N-2…1
优化 最好O(N) 最坏O(N^2)

void BubbleSort(int* a, int n)
{
	for (int j = 1; j <= n - 1; j++)
	{
		bool ExChange = false;
		for (int i = 0; i < n - j; i++)
		{
			if (a[i + 1] < a[i])
			{
				Swap(&a[i + 1], &a[i]);
				ExChange = true;
			}
		}
		if (ExChange == 0)
		{
			break;
		}
	}
	
}

快速排序-递归

快排的递归是一种先序

1. hoare版本
   

快速排序单趟干了两件事

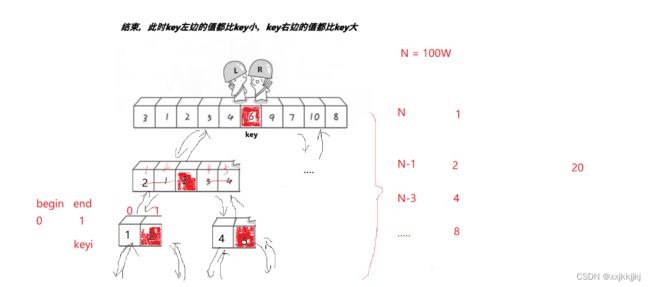
选出一个关键值/基准值key,把他放到正确的位置(最终排好序要蹲的位置)
左边的都比key小，右边的都比key大

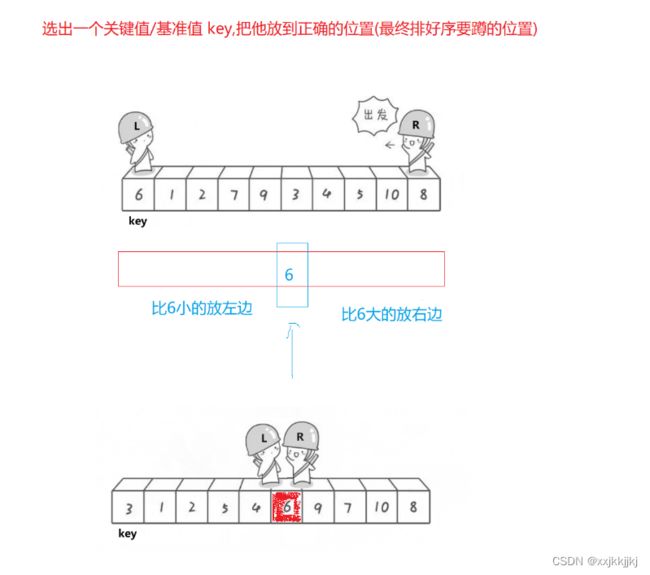
key一般选最左或者最右
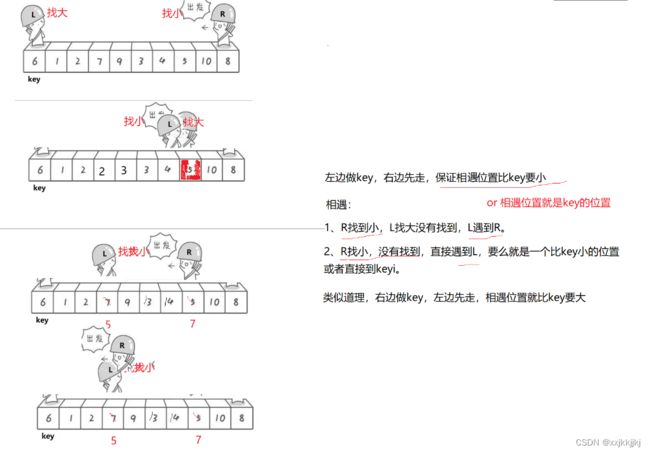
左边做Key 右边先走找小 左边后走找大，LR都找到就交换，直到LR相遇位置就是key应该排在的位置，把key和LR相遇位置交换，完成单趟排

为什么要右边先走找小，左边再走找大呢？
结论就是这样才能保证他们相遇时位置的值比Key小，或者就是key的位置

关键是发生交换后把小的换到左边
我们分类处理

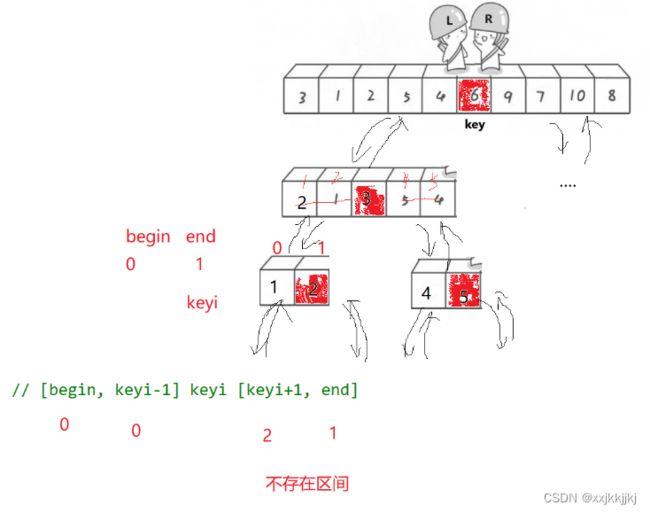
LR相遇后找到keyi应该排在的位置，根据keyi下标分出2个区间，继续递归下去,如果够均匀就是满二叉树了，思想也是二叉树前序递归的思想
[begin, keyi - 1] keyi [keyi+1, end]

递归返回条件是选出keyi 分出的区间只有一个值或不存在的区间

时间复杂度

如果能均分 就是满二叉树 高度次logN*单趟每次如图所示
二叉树最后一层占了总二叉树一半的节点数
假设N=100W就有20层
排到最后一层时，之前一半数量的节点都排好了，相当于最后一层 单趟N-50w 还是100W的量级

每层N-1 N-3 …减到最后一层N-50W 还是N的量级 所以说减不了多少，一共logN层 每层认为还是N
那就是O(NlogN)

数据有序时间复杂度反而最坏

最坏的情况 有序 反而变坏了 时间复杂度 N^2 等差数列
此时空间复杂度 是 O(N) 开辟了N个栈帧，平时空间复杂度是高度次O(logN)的栈帧（空间复用）

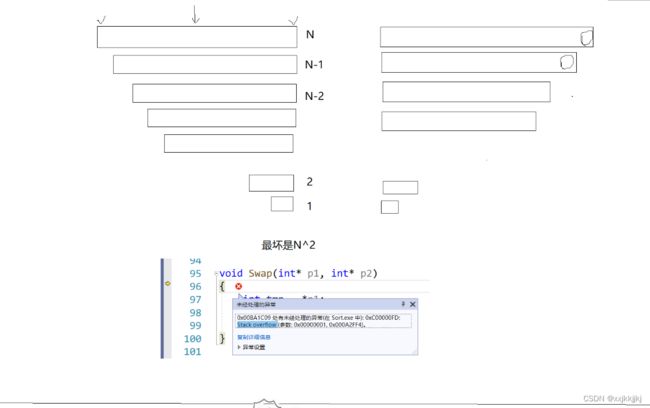
左边做key 123… 右边找不到比key小 R一直往左走
右边做key 7 6 5 … 1 左边找大 右边找小 R一直往左走

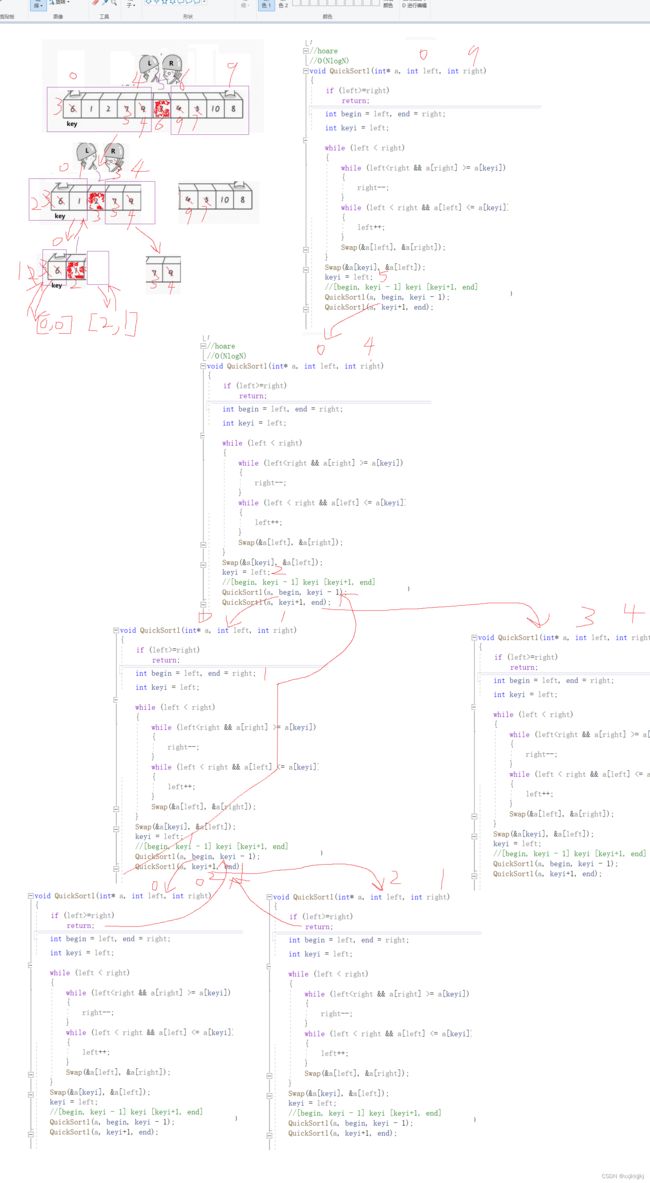
//hoare
//O(NlogN)
void QuickSort1(int* a, int left, int right)
{
	if (left>=right)
		return;

	int begin = left, end = right;

	//随机选key 
	//int randi = left + (rand() % (right - left));
	//Swap(&a[left], &a[randi]);

	//三目取中
	int midi = GetMidNumi(a, left, right);
	if(midi != left)
		Swap(&a[midi], &a[left]);

	int keyi = left;

	while (left < right)
	{
		while (left<right && a[right] >= a[keyi])
		{
			right--;
		}
		while (left < right && a[left] <= a[keyi])
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[keyi], &a[left]);
	keyi = left;
	//[begin, keyi - 1] keyi [keyi+1, end]
	QuickSort1(a, begin, keyi - 1);
	QuickSort1(a, keyi+1, end);
}

这就是hoare大佬研究出来的方法，其他方法都是这个大思想，单趟排出来的结果可能不一样，但是还是这个思想，选出key，左分小，右分大

2. 挖坑法

挖坑法和hoare 选出来的数有区别 ，但还是左边比key小，右边比key大

主要变化是单趟，搞了一个临时变量，和坑位，右边找到小R就变成新坑位，左边开始找大找到了也变成新坑位，直到相遇之后把临时变量Key放进去，区间被分成[begin, hole - 1] hole [hole+1, end]

//挖坑法
void QuickSort2(int* a, int left, int right)
{
	if (left >= right)
		return;

	int begin = left, end = right;

	//三目取中
	int midi = GetMidNumi(a, left, right);
	if (midi != left)
		Swap(&a[midi], &a[left]);

	int key = a[left];
	int hole = left;

	while (left < right)
	{
		// 右边找小
		while (left < right && a[right] >= key)
		{
			right--;
		}
		a[hole] = a[right];
		hole = right;

		// 左边找大
		while (left < right && a[left] <= key)
		{
			left++;
		}
		a[hole] = a[left];
		hole = left;
	}
	a[hole] = key;

	
	//[begin, hole - 1] hole [hole+1, end]
	QuickSort2(a, begin, hole - 1);
	QuickSort2(a, hole + 1, end);
}

3. 前后指针版本（最好）最简洁，好理解

单趟排出来和Hoare单趟也不太一样，但还是那个大思想
把比key大的值往右翻，比key小的值，翻到左边

//前后指针法
int PartSort3(int* a, int left, int right)
{
	//三目取中
	int midi = GetMidNumi(a, left, right);
	if (midi != left)
		Swap(&a[midi], &a[left]);

	int keyi = left;

	int prev = left;
	int cur = left + 1;
	while (cur <= right)//cur < right 外面是n-1 可能最后一个没比较
	{
		if (a[cur] < a[keyi] && ++prev != cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		++cur;
	}
	Swap(&a[keyi], &a[prev]);
	keyi = prev;

	return keyi;

}

快排优化

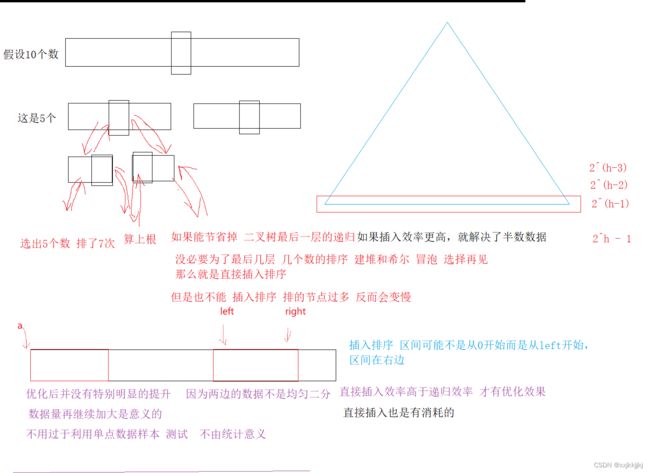
1. 小区间优化
   目的解决最后一层的递归次数过多，比如说下面左区间5个数排好递归了7次

要注意的就是插入排序的开始是a+left，还有闭区间要+1-[right-left+1]
会有一些提升，但是不明显，但是数据量加大后还是有一定作用的
我的理解是 虽然优化了后几层递归次数，但前面还是NlogN的时间复杂度，大概是半数数据

void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	//小区间优化--直接使用插入排序-优化后几层递归
	if (right - left + 1 > 10)
	{
		int keyi = PartSort3(a, left, right);
		QuickSort(a, left, keyi - 1);
		QuickSort(a, keyi + 1, right);
	}
	else
	{
		InsertSort(a+left, right - left + 1);
	}
	
}

解决有序数据的快排变慢

如果有序1，2，3，4…，左边选key或者右边选Key导致不能均分，使得快排效率变慢
2. 随机选key

	//随机选key 
	int randi = left + (rand() % (right - left));
	Swap(&a[left], &a[randi]);

范围是[left,right-1]这里面随机抽出一个来做key，注意到区间不是right，我试了下，如果选right在有序的情况下，一样烂

这种仍然能选到有序比如123…还是能选到1，但是数据量大了，纪律很小

3. 三目取中(更科学)
   [left,right]直接选出mid和left和right之中中间值，这样即使有序也可以均分了

int GetMidNumi(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[left] > a[mid])
	{
		if (a[right] > a[left])
		{
			return left;
		}
		else
		{
			if (a[mid] < a[right])
			{
				return right;
			}
			else
			{
				return mid;
			}
		}
	}
	else//a[left] < a[mid]
	{
		if (a[right] > a[mid])
		{
			return mid;
		}
		else
		{
			if (a[left] > a[right])
			{
				return left;
			}
			else
			{
				return right;
			}
		}
	}
}