水平集方法 level set method
The level set method was developed in the 1980s by the American mathematicians Stanley Osher and James Sethian. It has become popular in many disciplines, such as image processing, computer graphics, computational geometry, optimization, and computational fluid dynamics.
The level set method (sometimes abbreviated as LSM) is a numerical technique for tracking interfaces and shapes. The advantage of the level set method is that one can perform numerical computations involving curves and surfaces on a fixed Cartesian grid without having to parameterize these objects (this is called the Eulerian approach).Also, the level set method makes it very easy to follow shapes that change topology, for example when a shape splits in two, develops holes, or the reverse of these operations. All these make the level set method a great tool for modeling time-varying objects, like inflation of an airbag, or a drop of oil floating in water. 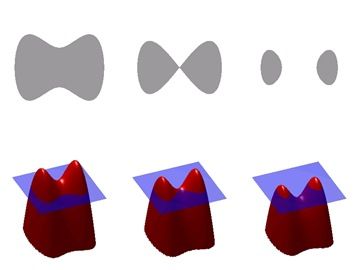
A very simple, yet powerful way to understand the level set method is by first studying the accompanying illustration before proceeding towards a more technical definition, which then becomes quite accessible. The figure on the right illustrates several important ideas about the level set method. In the upper-left corner we see a shape; that is, a bounded region with a well-behaved boundary. Below it, the red surface is the graph of a level set function ψ determining this shape, and the flat blue region represents the x − y plane. The boundary of the shape is then the zero level set of ψ, while the shape itself is the set of points in the plane for which ψ is positive (interior of the shape) or zero (at the boundary).
In the top row we see the shape changing its topology by splitting in two. It would be quite hard to describe this transformation numerically by parameterizing the boundary of the shape and following its evolution. One would need an algorithm able to detect the moment the shape splits in two, and then construct parameterizations for the two newly obtained curves. On the other hand, if we look at the bottom row, we see that the level set function merely got translated downward. We see that it is much easier to work with a shape through its level set function than with the shape directly, where we would need to watch out for all the possible deformations the shape might undergo.
水平集方法的基本思想是将界面看成高一维空间中某一函数ψ(称为水平集函数)的零水平集,且将界面的速度也扩充到高维的水平集函数上,然后写出水平集函数所满足的发展方程,求解此方程,推进水平集函数,计算到要求时刻,找出此新时刻水平集函数的零水平集,得到界面的形状,界面的法向方向,曲率等由水平集函数的偏导数容易算出。